上海市PM2.5与其他空气污染物动态关系的研究——基于VAR模型

(上海海事大学 上海 201306)

一、引言

(一)研究背景

随着经济飞速发展，大气污染问题也日益突出，全国各地频发的雾霾天气更是引起了广大民众和政府有关部门的高度重视。伴随着雾霾问题的发生，大气污染物PM2.5进入了公众视野。大气中PM2.5是一种可入肺的细颗粒物，它对人体会产生危害，引发疾病，也是引起雾霾问题、导致能见度下降的重要因素。

本文针对PM2.5与其它大气污染物所构成的动态系统，基于VAR模型，分析上海市PM2.5与其他空气污染物的动态关系，着重研究其它空气污染物对PM2.5的影响作用。

(二)变量选取和数据来源

城市中的空气质量具有不同的等级，而这个等级的确定会依据城市气体环境质量标准，空气质量的确定还会对相关的有害物质浓度值的范围有要求。

本文目的是分析上海市PM2.5与其他空气污染物的动态关系，故选取PM2.5、SO2、NO2、PM10、CO和O3作为研究变量。本文选取了上海市2018年1月1日至2019年的日度数据，数据均来源于国家环境保护部。在研究过程中，本文对所有指标均进行对数化处理得到新变量LPM、LSO2、LNO2、LPM10、LCO、LO3。

二、研究方法

向量自回归(VAR)模型是把系统中每一个内生变量作为系统中所有内生变量的滞后值的函数来构造模型，从而将单变量自回归模型推广到由多元时间序列变量组成的“向量”自回归模型，数学表达式为

yt=c+A1yt-1+…+Apyp-1+εt

(1)

其中：yt是 k 维内生变量向量，c是k维常数向量，p是滞后阶数，样本个数为T。k(k维矩阵A1，…，Ap和c是要被估计的系数矩阵。εt是k维扰动向量，假设(是εt的协方差矩阵，是一个k×k的正定矩阵。

Granger解决了x是否引起y的问题，主要看现在的y能够在多大程度上被过去的x解释，加入x的滞后值是否使解释程度提高。

由于VAR模型是一种非理论性的模型，因此在分析VAR模型时，往往是分析当一个误差项发生变化，这种分析方法称为脉冲响应函数方法。本文采用广义脉冲响应函数，即直接运用式(1)的无限移动平均形式，选择仅冲击其中一个变量，并根据过去的误差分布计算其它冲击的影响。

方差分解是通过分析每一个结构冲击对内生变量变化的贡献度，进一步评价不同结构冲击的重要性。

三、实证分析

(一)单位根检验

本文采用ADF方法进行单位根检验，最优滞后期的选择遵循AIC和SC信息量最小准则。结果LCO、LNO2、LO3、LPM、LPM10、LSO2的ADF检验值均小于临界值，所以它们是平稳的时间序列。

(二)VAR模型的构建和稳定性检验

确定最优滞后期对建立VAR模型尤为重要。本文利用LR取值最大、FPE、AIC、SC和HQ值最小准则来确定模型的最优滞后期。由计算结果综合考虑，本文选择最优滞后期为4，构建向量自回归模型VAR(4)。

对模型进行稳定性检验，得出AR特征多项式的根的倒数都在单位圆内，因此VAR(4)模型是稳定的，可利用该模型进行后续研究。

(三)格兰杰因果关系检验

为了确定SO2、NO2、PM10、CO、O3与PM2.5之间的长期静态关系，进行格兰杰因果检验。由表1，表明NO2和PM10是治理PM2.5问题的关键所在。

表1 格兰杰因果检验结果

(四)广义脉冲响应函数分析

建立VAR(4)模型基础上采用广义脉冲响应函数，选择滞后期为10，得到结果如图1。

SO2、NO2、PM10、CO正向冲击短期会引起PM2.5浓度值增长，随时间推移，影响逐渐消退。PM2.5浓度值的增长在第一期达到最大，第六期左右PM2.5浓度值的增长趋于稳定。PM10浓度值的短期变化对PM2.5浓度值增长有很大影响，PM10浓度值变化可以很好的预测PM2.5浓度值的变化。

O3前期会带来PM2.5浓度值的正增长，随时间推移增长速度变慢，后期会导致PM2.5浓度值的负增长。选取20作为滞后期。O3短期会引起PM2.5浓度值的增长，在第三期后变为负增长，说明O3对PM2.5浓度值有抑制作用。

NO2 PM10

O3 SO2

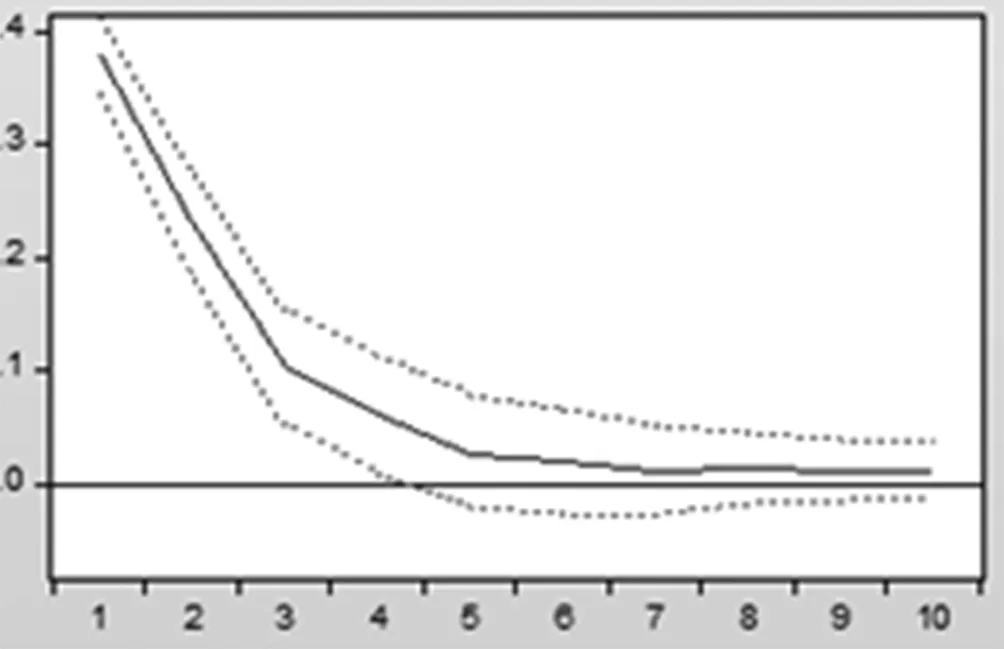
CO

(五)方差分解分析

对LPM进行方差分解分析。结果PM2.5在第一期只受自身和NO2的影响。NO2对PM2.5的影响作用不断加强，并在第九期方差贡献率达到最大。NO2对PM2.5影响加大。PM10和CO对PM2.5的方差功能贡献率也相对较大。

四、结论

NO2和PM10是PM2.5的格兰杰原因，其他空气污染物不是PM2.5的格兰杰原因，SO2、NO2、PM10、CO对PM2.5浓度值的影响持续时间长，说明PM2.5的治理需要有治理SO2、NO2、PM10、CO污染的各项措施配合才会有良好的效果，而O3前期会带来PM2.5浓度值的正增长，随时间推移增长速度变慢，后期会导致PM2.5浓度值的负增长；通过方差分解得到NO2对PM2.5影响最大且具有较长的滞后效应。