一种新的结合奖励机制的ETLBO算法
2019-11-28吴云鹏崔佳旭张永刚
吴云鹏,崔佳旭,张永刚
(吉林大学 计算机科学与技术学院,符号计算与知识工程教育部重点实验室,长春 130012)
近年来,群智能算法由于其收敛速度快、具有良好的适应性等特点,在工业调度[1]、网络服务优化[2]等领域应用广泛.目前较流行的新型群智能算法主要有:差分进化(differential evolution,DE)算法[3]、遗传(genetic algorithms,GA)算法[4]、粒子群优化(particle swarm optimization,PSO)算法[5]、蚁群优化(ant colony optimization,ACO)算法[6]、TLBO(teaching-learning-based optimization)算法[7-9]等.TLBO算法是一种模拟班级教学过程的新型智能算法.由于TLBO算法具有参数少、易实现、收敛速度快等优点[10],因此在机械参数设计[8]、连续函数优化[9]、平面钢架设计[11]等方面应用广泛.为进一步提高TLBO算法的性能,目前已有许多研究对其进行了改进,其中影响力最大的是ETLBO(elitist teaching-learning-based optimization)算法[12].在ETLBO算法中,根据成绩对学生进行排序,抛弃表现较差的学生,从而使算法一直向当前最优方向搜索.
本文针对ETLBO算法进行改进,通过引入奖励制度,给出相应的ETLBO-reward算法.在ETLBO-reward算法中,学生在“学”阶段能尽可能地选择表现更优的个体进行学习,从而提升算法的收敛能力.在ETLBO-reward算法的基础上,本文又提出一种简单的自适应精英个数策略——随机精英数策略,并提出了带奖励制度的自适应精英个数算法RETLBO-reward.最后,在RETLBO-reward算法的基础上又给出了一种离散的TLBO算法——D-RETLBO-reward.
1 TLBO算法
在TLBO算法中,将一组学生定义为一个种群.学生学习的科目对应经典优化问题中的决策变量,学习效果则对应优化问题中的适应度函数值.一个种群中学习效果最好的学生被定义为教师.决策变量包含在指定优化问题的目标函数中,最优解是具有最优目标函数值的学生对应所有科目的一组完全赋值.根据向不同身份人学习的方式,基本TLBO算法把学生的学习过程分为两个阶段:“教师教”阶段和“学生学”阶段,算法流程如图1所示.

图1 TLBO算法流程Fig.1 Flow chart of TLBO algorithm
“教师教”阶段:教师根据所负责科目的水平尽力提高全部学生在该科目成绩的平均值.假设有m个要学习的科目(即决策变量),n个学生(即种群大小),k为学生索引(k=1,2,…,n),j为科目索引(j=1,2,…,m).第i次迭代时,对于j个科目教师与所有学生学习成果的平均值差异如下:
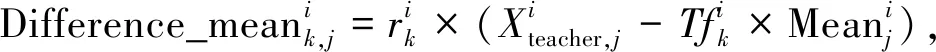
(1)


(2)
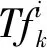

(3)
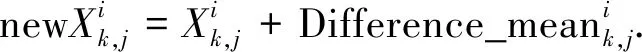
(4)
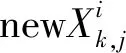

(5)
“学生学”阶段:学生主动向其他同学学习,以提高学习成果.学生k随机选择同学q作为学习对象进行学习:
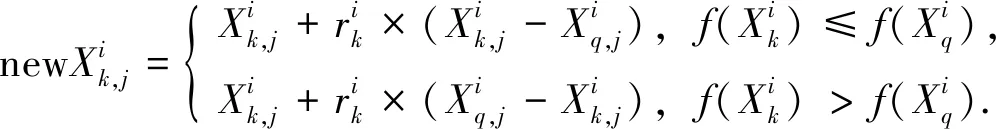
(6)
2 ETLBO算法
基于精英的TLBO(elitist TLBO algorithm,ETLBO)算法是受进化算法和群智能算法的启发,在基本TLBO算法中增加精英策略,以加速算法收敛.初始假设精英数为e,精英策略分为两个步骤:1) 算法每次迭代中,在“学”阶段后,选学习成果最好的e个学生和学习成果最差的e个学生,分别将他们确定为精英集(EliteSet)和差生集(WorstSet),用精英集替换差生集;2) 在替换差生集后,若出现冗余个体,则根据

(7)
进行修改,通过保证种群多样性避免陷入局部最优.其中:jr是随机整数(取值为[1,m]);Lowjr和Upjr分别表示第jr个决策变量的下界和上界.文献[13]的实验结果表明,ETLBO算法在求解连续非线性优化问题方面明显优于粒子群优化、差分进化、人工蜂群等算法.
3 基于奖励制度的ETLBO算法
3.1 ETLBO-reward算法
ETLBO算法在“学”阶段,一个学生选取另一个学生通过式(6)进行差异学习,选取过程是随机的,从而可能出现学习成果差的学生寻找的学习对象也可能是差生集的情形,使学习成果提高较小甚至未提高.为了加强除精英学生外的学生学习程度,本文在ETLBO算法的基础上引入奖励制度:
1) 对表现好的学生给予奖励;
2) 在“学”阶段根据获得的奖励通过轮盘赌方法选择学习对象.
学生Xk在第i次迭代获得的奖励定义为
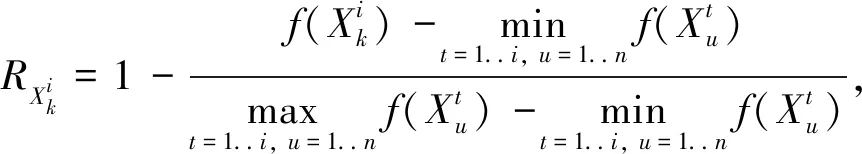
(8)
ETLBO-reward算法.
输入:学生个数n,科目数m,精英个数elitist,最大迭代次数MAXITER,每个科目对应的上下界Upj和Lowj;
输出:最优解;
步骤1) FORkin 1..nDO
步骤2) 按式(7)对学生Xk的所有科目初始化;
步骤3) 计算f(Xk)和RXk,并把RXk加入Xk的奖励队列中;
步骤4) END
步骤5)Xteacher←getTeacher( );
步骤6) WHILE当前迭代次数i≤MAXITER DO
步骤7) FORkin 1..nDO
步骤8) FORjin 1..mDO
步骤12) END
步骤13) 边界检查;
步骤15) IF更新THEN
步骤17) END
步骤18)h←根据奖励的平均值进行轮盘赌选择得到一个学习对象;
步骤(20) 边界检查;
步骤22) IF更新THEN
步骤24) END
步骤25) END
步骤26) 得到elitist个精英学生EliteSet;
步骤27) 得到elitist个差生学生WorstSet;
步骤28) FORuin 1..elitist DO
步骤29)XWorstSet[u]←XEliteSet[u];
步骤30) 根据式(7)修改冗余;

步骤32) END
步骤33) WHILE 存在相同的学生p和qDO
步骤34) 根据式(7)修改冗余;
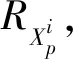
步骤36) END
步骤37) END.
ETLBO-reward算法的步骤1)~4)为初始化阶段;步骤5)根据学习成果优劣得到表现最好的学生赋给Xteacher;步骤6)~36)是整个迭代过程,步骤6)的终止条件是迭代次数达到规定的最大迭代次数MAXITER;步骤8)~17)为算法的“教”阶段,其中步骤8)~12)是学生k的差异学习阶段,步骤13)是边界检查阶段:
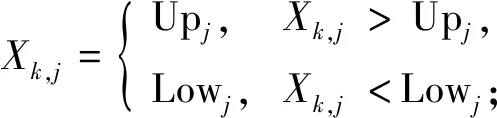
(9)
3.2 RETLBO-reward算法
4 实验结果与分析
实验环境为:ubuntu 14.04 LTS 64位操作系统,Intel i7-3770处理器,8 GB内存.连续非线性优化问题测试集采用较流行的CEC08中6个测试函数F1,F2,F3,F4,F5,F6[14].TLBO算法种群规模设为50,最大评估函数次数为240 000.可根据
noef=2×NP×Iter,
(10)
noef=2×NP×Iter+de_noef
(11)
分别计算出TLBO和ETLBO算法的函数评估次数.其中:noef表示函数评估次数;NP表示种群大小;Iter表示迭代次数;de_noef表示去掉重复的函数评估次数.
TLBO和ETLBO算法函数评估次数的计算只相差变异重复个体的函数评估次数,因此在确保满足评估次数公平的前提下,本文设置TLBO算法和ETLBO算法的最大迭代次数为2 400和2 300,从而可保证两种算法函数评估的最大次数都近似为240 000.取ETLBO算法的精英个数为4,8,12,16,20,24.每种算法在每个测试函数上都运行10次.表1为TLBO算法和ETLBO算法的参数设置.表2~表7分别为TLBO基本算法、ETLBO算法和ETLBO-reward算法在测试函数F1~F6上的对比结果.其中,B,W,M,SD分别表示算法10次运行的最好解、最坏解、平均解、标准差.

表1 TLBO算法和ETLBO算法的参数设置

表2 不同算法在测试函数F1(-450)的对比结果

续表2

表3 不同算法在测试函数F2(-450)的对比结果
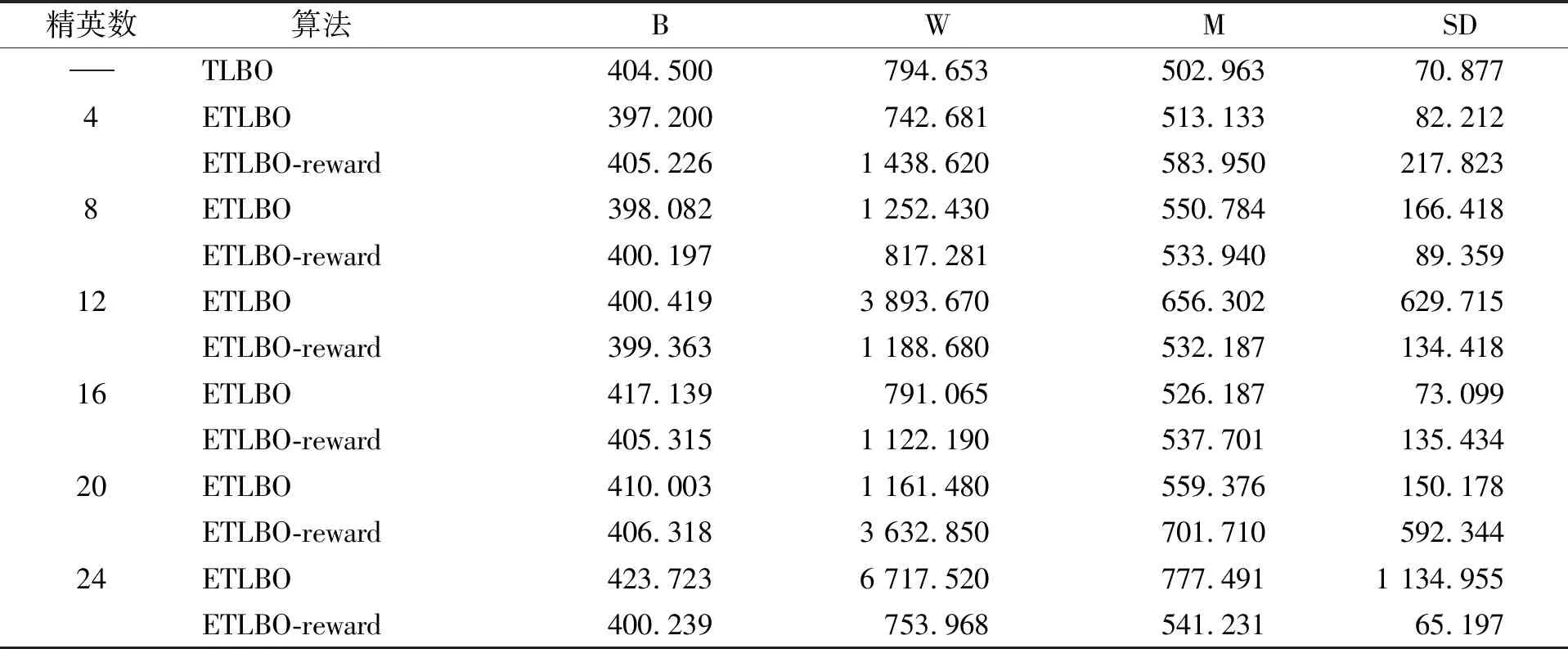
表4 不同算法在测试函数F3(390)的对比结果

表5 不同算法在测试函数F4(-330)的对比结果
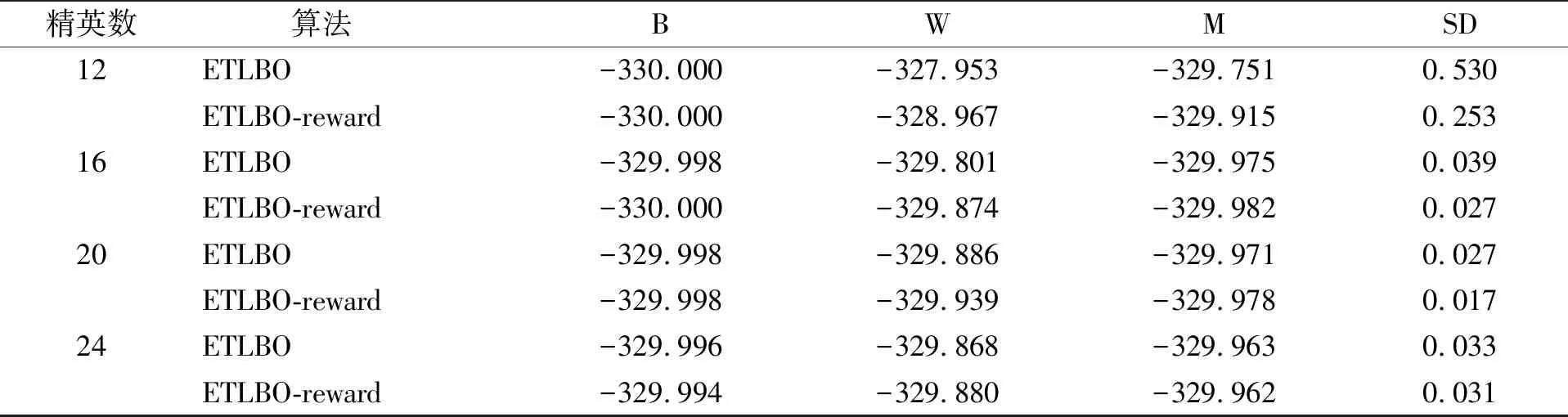
续表5
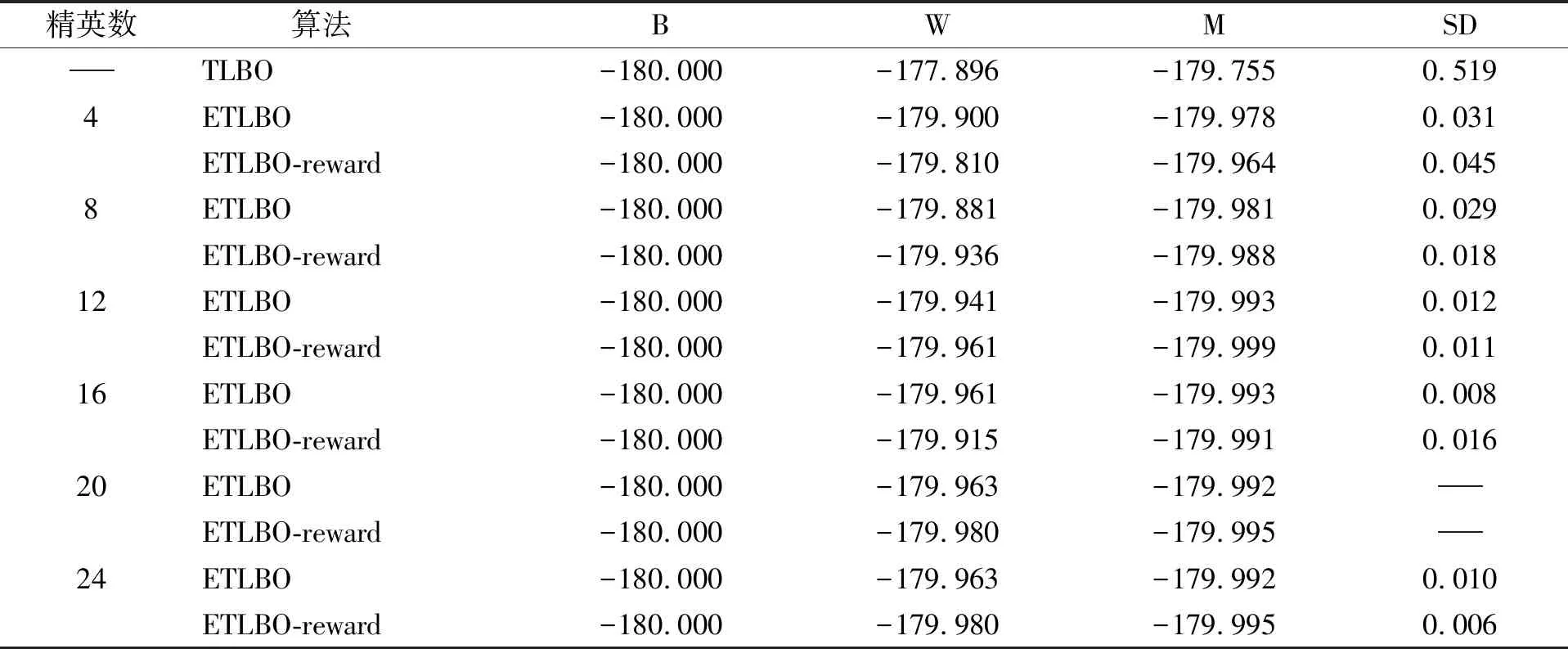
表6 不同算法在测试函数F5(-180)的对比结果

表7 不同算法在测试函数F6(-140)的对比结果
由表2~表7可见,F1~F6测试函数中,ETLBO算法和ETLBO-reward算法都能求出比TLBO算法更高质量的解;在测试函数F1中,ETLBO算法和ETLBO-reward算法均能求出最优解,但ETLBO-reward算法比ETLBO算法更稳定;在测试函数F2中,ETLBO-reward算法的平均求解质量优于ETLBO算法;在测试函数F3中,ETLBO-reward算法和ETLBO算法表现相近,但当精英个数为8,12,24时,ETLBO-reward算法求解稳定性明显优于ETLBO算法;在测试函数F4~F6中,ETLBO-reward算法在求解质量和稳定性方面均优于ETLBO算法.
表8为TLBO,ETLBO,ETLBO-reward和RETLBO-reward算法在F1~F6测试函数上的对比结果,分别用A1,A2,A3和A4表示TLBO,ETLBO,ETLBO-reward和RETLBO-reward算法.ETLBO算法与ETLBO-reward算法是分别选择在每个测试函数上表现最好的结果.由表8可见:在测试函数F3上,ETLBO算法表现最好;在函数F5上,ETLBO-reward算法表现最好;在测试函数F1,F2,F4,F6上,RETLBO-reward算法整体上优于其他算法.

表8 不同算法在6个测试函数上的对比结果
综上所述,本文针对ETLBO算法进行优化,通过提出一种奖励机制,在“学”阶段学生有更大的概率向优秀个体学习,从而加快收敛速度.根据该机制提出了相应的ETLBO-reward算法,并提出一种简单的自适应精英个数RETLBO-reward算法.实验部分应用ETLBO-reward算法和RETLBO-reward算法求解连续非线性函数F1~F6.实验结果表明,ETLBO-reward算法在整体上优于ETLBO算法,并且RETLBO-reward算法在省略了确定精英个数过程的同时保证了较好的求解效率.
