高阶强伪单调映射变分不等式解的性质
2019-11-28韩文艳余国林
韩文艳,余国林
(北方民族大学 应用数学研究所,银川 750021)
0 引 言
令X为一实Hilbert空间,用〈·,·〉表示X中的内积,〈·,·〉诱导出的范数记为‖·‖.假设C⊂X为一非空闭凸子集,Φ:C→X为一映射,考虑如下变分不等式问题:

变分不等式问题VI(C,Φ)在力学、控制论、经济数学、对策论、微分方程和最优化理论中应用广泛,解的存在性是研究变分不等式问题VI(C,Φ)的热点之一.在讨论变分不等式解的性质时,通常需要映射Φ满足一定的连续性和单调性假设[1-6].Kien等[2]在映射Φ满足弱连续和伪单调的条件下,得到了问题VI(C,Φ)解存在的等价条件,但仅给出了解的存在性,未讨论解的唯一性问题.本文通过对映射Φ引进一类高阶单调性的概念,在这类高阶单调性假设下,考虑问题VI(C,Φ)解的唯一性.
在构造数学模型解决实际问题的过程中,由于用观察、实验和测量等方法所获得的数据不可能完全准确,因此所得的数学模型和实际问题的真实模型一般存在一定的差异,后者通常称为精确模型,前者称为近似模型.近似模型可视为由精确模型中的数据做微小变动而得到.当将一个具有精确模型变分不等式的数据做微小变动后,所得到的近似模型变分不等式不仅要有解,而且解也只有微小变化,因为只有这样才能用近似模型代替精确模型,此即为变分不等式解的稳定性理论[7-8].本文在映射的高阶单调性假设下,研究变分不等式问题VI(C,Φ)解的稳定性.
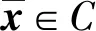
1 高阶强伪单调性及解的存在定理
定义1令D为Hilbert空间X中一非空子集.
1) 如果存在常数α>0,使得
〈F(x)-F(y),x-y〉≥α‖x-y‖2, ∀x,y∈D,x≠y,
则映射F:D→X在D上称为强单调的;
2) 如果存在常数α>0,使得
∀x,y∈D,x≠y, 〈F(x),y-x〉≥0 ⟹ 〈F(y),y-x〉≥α‖x-y‖2,
则映射F在D上称为强伪单调的;
3) 如果存在常数α>0,使得
∀x,y∈D,x≠y, 〈F(x),y-x〉≥0 ⟹ 〈F(y),y-x〉≥0,
则映射F在D上称为伪单调的.
定义2令D为Hilbert空间X中一非空子集.如果存在常数α>0,使得
∀x,y∈D,x≠y, 〈F(x),y-x〉≥0 ⟹ 〈F(y),y-x〉≥α‖x-y‖m,
则映射F:D→X在D上称为m-阶强伪单调的.此时,也称F在D上关于常数α是m-阶强伪单调的.
注1显然,如果F:D→X在D上是m-阶强伪单调的,则F在D上是伪单调的;在定义2中取m=2,则F是D上强伪单调映射的.
下面举例说明高阶强伪单调映射的存在性.
例1令X=,D=[0,+∞),函数F:D→,定义为F(x)=x3.下面验证F在D上关于常数α=1是4-阶强伪单调的.事实上,假设〈F(y),x-y〉=y3(x-y)≥0,则有
下面考虑变分不等式问题VI(C,Φ),用Sol(C,Φ)表示问题VI(C,Φ)在C上解的集合.文献[2]在映射Φ为弱连续和伪单调假设下,给出了问题VI(C,Φ)解的存在性定理:


(1)
为一有界集,则问题VI(C,Φ)有解.
定理1令X为Hilbert空间,C⊂X为一闭凸集.假设Φ:C→X在C上弱连续并且m-阶强伪单调,则问题VI(C,Φ)存在唯一解.

由Cauchy-Schwrz不等式,可得
所以有

(2)
式(2)表明

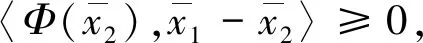
(3)
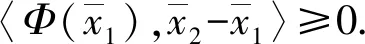

(4)
2 高阶强伪单调变分不等式解的稳定性
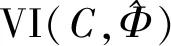
引理2[11]令C⊂n为一闭凸集,Φ:C→n在C上连续.假设存在向量使得式(1)为一个有界集.如果U⊂n为任意开集,且满足Sol(C,Φ)⊂U,则变分不等式问题在U上有解,其中n为一连续映射,且存在δ>0,使得


定理2令C⊂n为一闭凸集,Φ:C→n在C上弱连续并且m-阶强伪单调.令为问题VI(C,Φ)的唯一解.则对任意的ε>0,变分不等式问题在上有解,其中n为一连续映射,且存在δ>0,使得

(5)


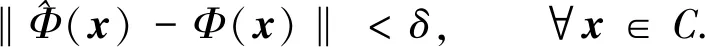
(6)

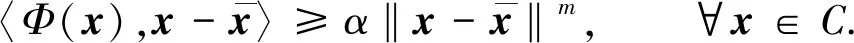
(7)
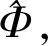
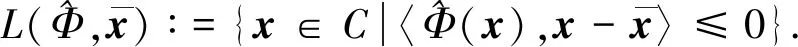
(8)
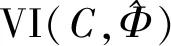
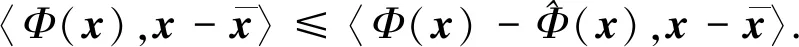
(9)
由Cauchy-Schwarz不等式并结合条件(6),可得
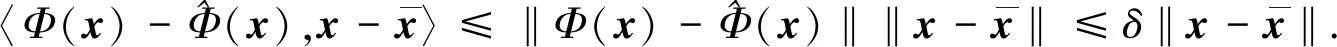
(10)

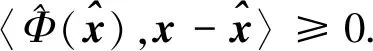
(11)
3 高阶强伪单调变分不等式的全局误差界
引理3[12]令C是Hilbert空间X中的一非空闭凸子集.对任意的x∈X,存在唯一的PC(x)∈C(PC(x)称为x到C的投影),使得
‖x-PC(x)‖≤‖x-y‖, ∀y∈C,
并且
〈x-PC(x),y-PC(x)〉≤0.
反之,如果x′∈C,并且
〈x-x′,y-x′〉≤0, ∀y∈C,
则有PC(x)=x′.
定义3[1-3]令D为Hilbert空间X中的一非空子集.如果存在常数L>0,使得
‖F(x)-F(y)‖≤L‖x-y‖, ∀x,y∈D,
则映射F:D→X在D上称为L-Lipschitz连续的.
定理4令C是Hilbert空间X中的一非空闭凸子集.假设映射Φ:C→X在C上是L-Lipschitz连续,并且关于常数α>0是m-阶强伪单调的,则有

(12)


(13)
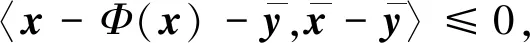
这等价于

(14)

再结合式(14),可得
即
再利用Cauchy-Schwarz不等式,可得
因此有
最后,由三角不等式可得
证毕.
