基于COMSOL的拓扑优化及联合仿真
2019-11-28赵重年王文强
王 曦,赵重年,王文强
(1.陆军军事交通学院研究生队,天津300161;2.陆军军事交通学院军事交通运输研究所,天津300161;3.陆军军事交通学院,天津 300161)
拓扑优化是根据负载情况、约束条件(如应力、位移、频率和重量等)和性能指标(刚度、重量等),利用有限元分析和优化方法,使设计域达到最优材料布局的一种结构优化方法[1]。目前,连续体拓扑优化的研究已经较为成熟,现有的商业有限元软件基本都可以进行拓扑优化,但每款软件的优化模块各有区别,关于参数的设置也多种多样,通用性较差,同时,对用户的使用要求较高,不适于拓扑优化的利用和推广,一定程度上迟滞了结构优化的发展,因此,提高拓扑优化的在仿真中的通用性和工程应用中的应用效率对结构优化具有重要意义。
1 拓扑优化基本理论
1.1 变密度法
结构优化设计是用系统的、目标定向的过程与方法代替传统设计,其目的在于寻求既经济又适用的结构形式,以最少材料、最低造价实现结构的最佳性能。一般地,优化问题的数学模型可表示为:

式中:X为设计变量,f(X)为目标函数,gi(x),hj(x)为约束条件。
假设设计域由有限个单元组成,变密度法的基本思想就是定义一种密度可变的材料单元填充设计域,取值定义在(0,1)区间内,取0表示孔洞,取1表示实体,则优化问题转变为0-1问题。
在拓扑优化中,希望优化后的结构在保持最大应力承受极限的情况下质量减少,对于大多数工程上的零件,均采用统一结构制造,则质量最小可以等价为体积最小。优化的目标一般是结构的刚度,为了在数学上方便凸优化计算,将刚度最大等效为柔度最小,其模型表达为:

式中:C(x)为柔度,V 为设计域初始体积,f为体积约束因子。
1.2 插值模型
变密度法定义一个经验公式(式)来表达相对密度与弹性模量E的非线性关系,通过这种关系使设计变量与目标函数产生联系,则结构拓扑优化问题转化为材料的最优分布问题。
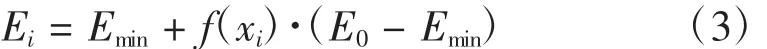
式中,f(xi)又称为材料插值模型,设计变量xi控制着材料的取舍,为了更好的获得拓扑结构的形状和边界,插值模型应使xi的取值向区间两端分化。目前,应用最为广泛的两种插值模型为SIMP模型[2](式)和RAMP[3]模型(式):

两种模型都是通过引入惩罚系数,使得变量更快的逼近端点值,前者采用指数函数的形式,引入惩罚因子p,后者采用有理数函数的形式,引入权重因子q。两者性能由图1可知。

图1 两种材料插值模型惩罚效果图
2 COMSOL中的拓扑优化
2.1 优化目标与约束条件的设置
在考虑结构优化的问题时,需要特别注意,对复杂工程结构的拓扑优化是一个计算量相当大的问题,因此,在软件中实现优化时要进行模型简化和等效条件转化。
(1)目标函数
拓扑优化的目标函数一般为刚度最大,即柔度最小。用结构在极限条件下的总变形能来表示结构刚度最大时的状态。应变能可以精确的平衡载荷所做的功,因此,应变能最小可以使施加载荷所引起的位移最小,有效地得到柔顺性最小的目标。
通过有限元知识可知,结构的总变形能为各个单元变形能量的总和。对由微小体元dΩ=dxdydz组成的结构体,在受到各个方向的正应力和切应力时的应变能为:

COMSOL中对于应变能的描述体现为指标形式,如公式:
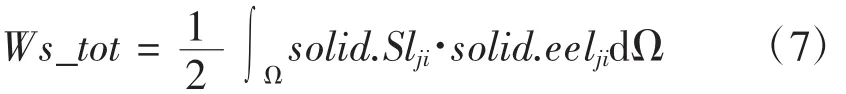
式中:solid.Sl为应力,solid.eel为应变。
优化过程中,定义当前结构应变能与初始应变能的比值Ws/Ws0为目标函数,则比值最小表示结构刚度最大。
(2)约束条件
从概念上讲,拓扑优化只是最小化所用材料的数量,以初始设计域的体积分数来定义约束条件为:

式中:f为体积分数,V为初始设计域的体积。
2.2 拓扑优化中的密度模型及不稳定现象的处理
在COMSOL中的拓扑优化模块中,建立了变密度法为基础的密度模型,用户可以根据需要选择SIMP或RAMP材料插值模型。设计变量相对密度xi用材料体积因子θ表示,即每个单元格实体材料的体积占比。
此外,在拓扑优化中,会出现一些与模型本身无关的数值不稳现象,主要有中间密度单元,棋盘格式现象,网格依赖性等。
对于棋盘格现象和网格依赖性,较为常用的方法是敏度过滤法,通过提取相邻单元信息,对当前单元的取值产生影响,距离越近,影响越大。但是对相邻单元提取信息的计算量相当庞大,COMSOL中采用Sigmund提出的亥姆霍兹过滤器作为敏度过滤的改进方案[4],仅需要提取所需单元的网格信息,用最小过滤半径与体积因子的拉普拉斯算子的乘积对材料体积因子进行过滤,提高了计算效率。

式中:θf表示过滤后的材料体积因子;θc表示系统控制的材料体积因子;Rmin表示最小过滤半径,一般取最小网格的1/2或1/4。
将过滤后的设计变量进行投影,可以减少中间密度单元[5]。选择基于双曲正切函数的投影可以得到较为清晰的拓扑图像(如公式10)。

式中:β表示投影斜率,θβ表示投影点。
2.3 参数对优化结果的影响
本文通过二维MBB梁结构在的拓扑优化讨论惩罚因子p和投影斜率β对优化结构的影响。如图2为MBB梁结构,矩形梁长6 m,高1 m,两端支撑,中间施加垂直向下300 kN的力,结构材料为普通钢铁,设置体积因子上限为0.5。

图2 MBB梁几何模型
相同条件下,表格1为惩罚因子p取2~5时的优化结果对比。
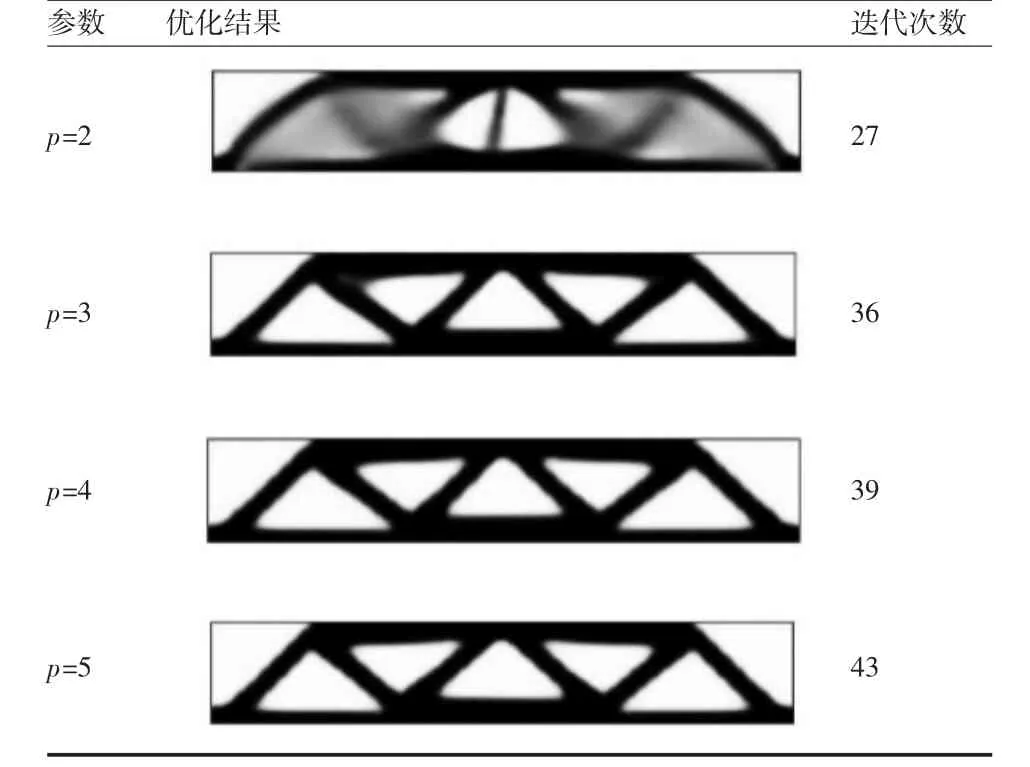
表格1 惩罚因子对MBB梁拓扑优化结果的影响
由表中图像可知,惩罚因子的增大可以控制灰度单元,得到更加清晰的拓扑边界。也就是说,p值可以取到足够大,以获得足够清晰的边界。但同时迭代次数也相应增多,计算时间变长,收敛速度减慢,两者相互矛盾。工程中,一般取p=3,使得优化结果较为清晰的同时也能保证计算效率。
β作为双曲正切投影的关键参数,控制着结果整体的清晰度,在相同条件下,分别取β为1~12时的结果进行评估,图3选取了5个取值的优化结果,图4为迭代次数变化趋势。
由上图表可知,受双曲正切函数性质的影响,随着投影斜率的增大,收敛速度加快,图像也更加清晰,但当β大于8时,迭代次数趋于平稳,不再减少,且结构出现奇异,不能得到正确的拓扑结构,因此,β一般取8最为合适。
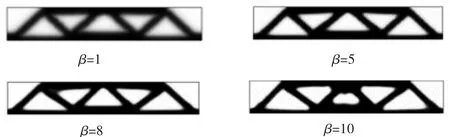
图3 β取不同值时对MBB梁拓扑优化结果的影响
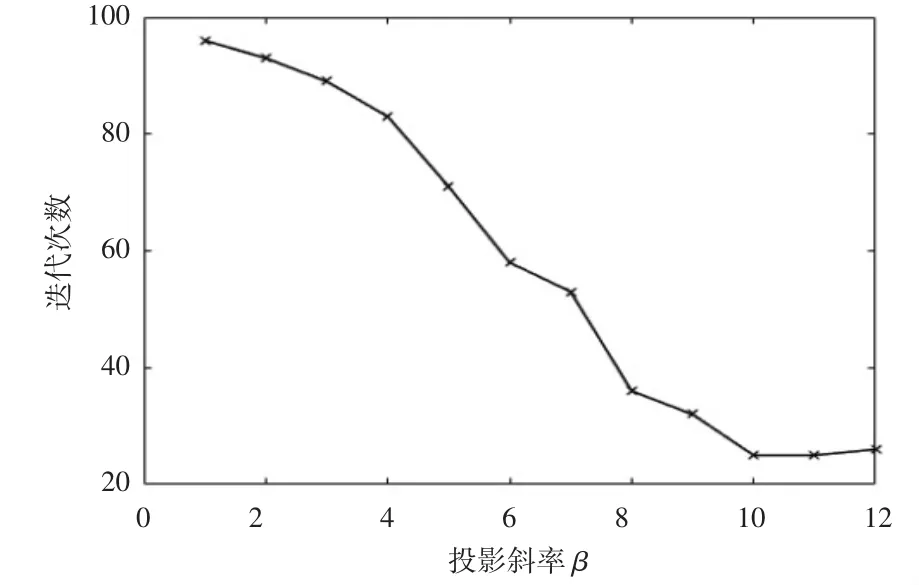
图4 β取不同值时对MBB梁拓扑优化的求解迭代次数
3 联合仿真
由上文可知,对于COMSOL中的拓扑优化大致分为两个步骤,第一步是对原结构的分析,得到初始结构的应变能参考值,第二步才是拓扑优化的相关设置。繁琐的二次设置势必会影响工作效率,因此,如果将拓扑优化的关键步骤集成在一个程序内,那么对于一般的结构,只要完成其相应的前处理,就可以方便地实现优化。
3.1 对一般结构优化的实现
COMSOL源自于MATLAB的工具箱(原FEMLAB),通过其自身的APL语法,将从建模开始的所有步骤编入MATLAB中,再与控制语句相结合,实现模型的各种后处理。
首先,在COMSOL界面中完成初始结构模型的前处理,包括几何模型搭建,材料、边界条件和网格的设置,保存为.m文件,通过MATLAB控制语句调节程序流程,对初始结构进行有限元分析。然后,将第一步分析得到的结构应变能提取出来,作为参数放入第二步优化中。最后,在MATLAB中调试好优化求解器进行求解。本程序设置体积约束、惩罚因子、投影点、投影斜率、优化域及非优化域等6个参数,也可以根据需要进行添加或减少。
对于优化的结果,可以在MATLAB的图片查看器中分析,也可以将结果连接到COMSOL界面中进行处理。
3.2 几种结构的测试
为了检验程序的可行性和通用性,通过几种典型的三维结构测试程序的优化结果。
3.2.1 L型负载梁
如图5,三维结构L型梁长宽比为0.9,厚度为0.1 m。梁的上端固定,右侧施加一个垂直向下的载荷,材料为钢铁,体积约束为0.3。其优化结果如图5所示。

图5 L型负载梁结构及拓扑优化结果
由优化结果可看出,在L型梁的上半部分只保留了两侧的受力悬臂,下半部分得到3个大小不等孔洞,其内部基本掏空,只保留了部分连接两个表面的结构。拓扑结构较为清晰,边界明显,孔洞虽然较为规律,仍有优化空间,整体来看,是比较成功的优化结果。
3.2.2 简单悬臂梁
如图6所示,三维结构悬臂梁,长0.8 m,高0.5 m,厚0.1 m。悬臂梁一端固定,另一端施加一个垂直向下的变载荷,材料为钢铁,体积约束为0.5。其优化结果如图6所示。
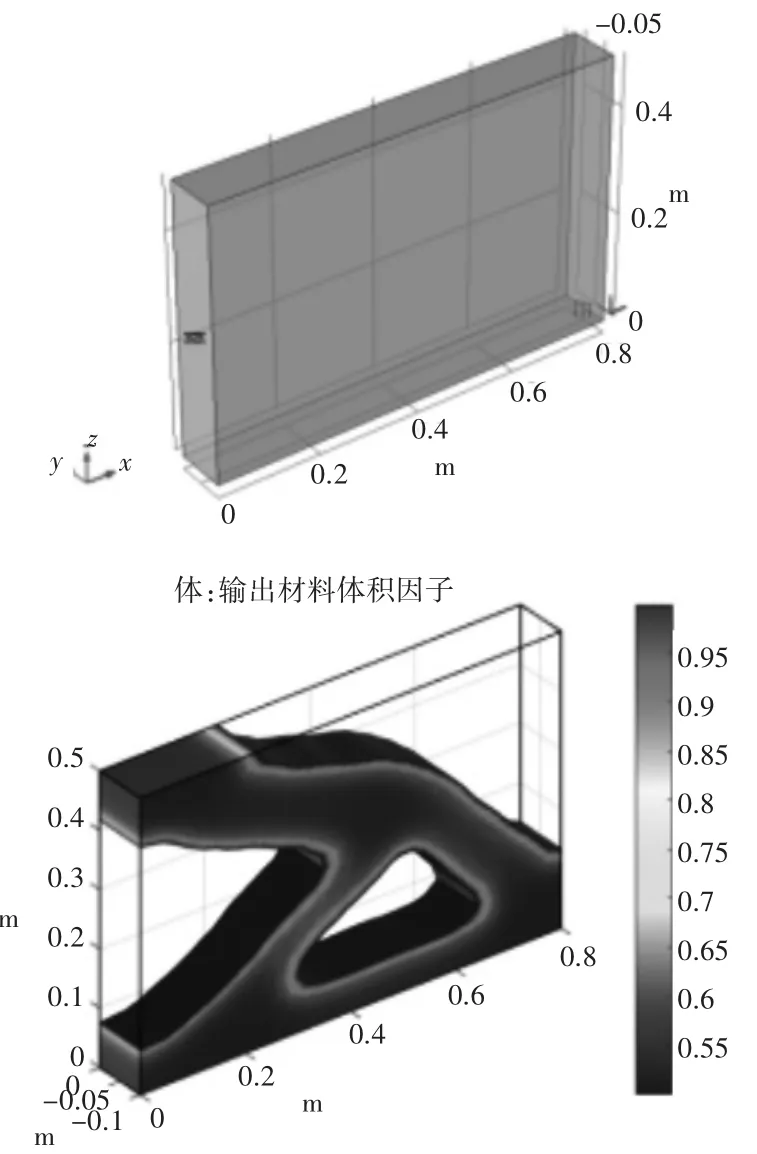
图6 悬臂梁结构及拓扑优化结果
由优化结果可看出,梁的右上角由于受力较小,全部挖空,中间掏出一个三角形的孔洞,整体呈现桁架结构,符合实际物理情况,同样是比较成功的优化结果。
由上两例优化结果可看出,本程序拓扑优化的结果为整体结构的概念形状,对于边界的处理较为粗糙,虽然不适于实际的生产加工,但其作为工程设计的初始结构是可以接受的。可以以此优化结果为基础,建立参数化模型,根据具体的载荷大小和实际工艺,对结构进行形状优化和尺寸优化。
4 结束语
本文研究了基于变密度法的拓扑优化理论及在COMSOL软件中的应用,讨论研究了几种重要参数对优化结构的影响,得出了最佳的设置方案,并利用MATLAB将COMSOL中繁琐的操作集成到一个程序中,开发了可以对一般结构实现拓扑优化的通用程序,从而为工程设计人员提供可靠的、指导性的结构设计方案,避免了复杂繁琐设计步骤,提高了程序的普适性,缩短了设计周期,对工程设计有一定促进意义。
