双磁悬浮振子结构地铁轨道监测小波分析*
2019-11-27赵彦超王德玉
江 东,赵彦超,王德玉
(哈尔滨理工大学电气与电子工程学院,哈尔滨 150080)
地铁机车在线振动测量效率较高,可以对地铁轨道状况进行实时监测[1],该振动测量属于绝对式振动测量[2]。测量原理是利用质量块自身的惯性性质,当被测振动物体振动频率超过一定数值时,惯性质量块相对于绝对参照系不动,质量块与仪器壳体之间的相对位移变化与被测振动体的振动幅值近似成正比,相位相反,从而实现振动测量。
传统绝对式振动测量一般采用电涡流式[3]、压电式[4-5]、电容式[6]、电感式[7]等测量方法,作为惯性质量块的振子通过弹性部件与模型壳体相连接,由于具有弹簧部件[8-9],且存在摩擦,测量灵敏度不高。地铁机车行进方向的加速度虽然很高,但垂直方向振动幅值较小,需要更高的测量灵敏度。国内外科学家在绝对振动测量原理的基础上,将新材料、新技术引进至振动测量中。最新的光纤、光栅测量方法可以实现绝对式振动测量。以光折变晶体硅酸铋为记录介质,基于反射式全息光栅零差干涉原理构成振动测量系统,其测量灵敏度高于透射式全息光栅振动测量系统[10]。利用光纤、光栅构成的传感器可实现电动机叶片振动测量,还可通过光纤传感器测量钢桥的振动[11],但成本高、需要干涉仪等设备、安装调试比较困难。
纵观国内外研究现状和趋势,惯性式振动测量技术及设备在不同的工程技术领域中得到了广泛地应用。但是由于结构和材料的限制,在运行性能上还受到了一定的局限,不能满足一些工程的需要。本文在这些研究的基础上,针对现存的问题,提出以磁悬浮技术测量振动的方案,磁悬浮技术可以使测量系统的振子悬浮于空中,可测量较低的加速度振动信号[12-14],结构简单,测量灵敏度高,适于地铁机车的振动测量。
1 双磁悬浮振子结构模型及工作原理
为了提高振动测量系统的灵敏度,采用双磁悬浮振子结构构成振动测量系统,双磁悬浮振子结构见图1所示。

图1 双磁悬浮振子结构模型
设计的双磁悬浮振子结构应用在绝对式振动测量中。振动测量时,将仪器壳体与被测振动体刚性固接。地铁机车振动测量时将其固定在机车车厢中间位置。双磁悬浮振子结构模型中定子与仪器壳体固接在一起。安装时,定子、振子1和振子2磁极相互排斥。地铁机车有振动时,定子随仪器壳体与地铁机车一起振动,磁悬浮振子1和磁悬浮振子2因惯性,在被测振动超过一定频率时相对绝对参照点不动,振子1和振子2与仪器壳体将产生相对位移。根据绝对式振动测量理论,该相对位移与被测物体振动幅值近似相等,相位相反。红外发射器和红外接收器中心点安装在振子2上切面的位置,实现相对位移的测量。
设计的双磁悬浮振子结构应用在绝对式振动测量中。振动测量时,将仪器壳体与被测振动体刚性固接。地铁机车振动测量时将其固定在机车车厢中间位置。双磁悬浮振子结构模型中定子与仪器壳体固接在一起。安装时,定子、振子1和振子2磁极相互排斥。地铁机车有振动时,定子随仪器壳体与地铁机车一起振动,磁悬浮振子1和磁悬浮振子2因惯性,在被测振动超过一定频率时相对绝对参照点不动,振子1和振子2与仪器壳体将产生相对位移。根据绝对式振动测量理论,该相对位移与被测物体振动幅值近似相等,相位相反。红外发射器和红外接收器中心点安装在振子2上切面的位置,实现相对位移的测量。
无振动时,设振子1与定子之间的距离为y10,振子2与振子1之间的距离为y20。当机车有振动时,双磁悬浮振子结构模型状况发生变化。
设计双磁悬浮振子是为了提高振动测量的灵敏度。图1中假定机车向下运动,定子的绝对位移为Δx,振子1相对位移为Δy1,振子2与振子1之间的相对位移为Δy2。
2 振子的振动方程
振子的振动方程通过牛顿第二定律建立。为建立振动方程,需要测定振子所受磁斥力与位移的关系。首先测定振子悬浮距离y0,然后在振子上加锡等非铁磁性物体作为向下施加的力,测定平衡时振子的悬浮距离。
实测斥力与两永磁体间距关系如表1。

表1 位移与振子所受斥力的关系
通过MATLAB最小二乘法函数拟合得到斥力与两永磁体间的距离之间的函数曲线[15-17],见图2。

图2 力与位移函数关系
得到振子所受磁斥力与位移的关系式[18]:
(1)
在平衡点附近进行线性化处理,进行泰勒级数展开:
f(y)=0.028 42-1.593 9Δy
(2)
根据振动工程理论,阻尼力与速度成正比且方向与振子运动方向相反。阻尼力主要由空气阻尼以及铝板的电磁阻尼产生的。当振子自由振荡时,振子的自由振动方程为:
(3)
式中:m为振子的质量,c为阻尼力的比例系数,k为弹性系数。各项除以m,变换为:
(4)
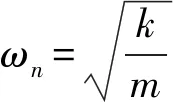
c=2ξωnm
(5)
当振子处于自由振荡时,测得振子的固有振荡周期为T=268 ms,即固有角频率为ωn=23.4 rad/s,阻尼率ξ=0.6,由此,得到阻尼比例系数:c=0.084 Ns/m。
根据牛顿第二定律,振子的运动方程为:
(6)
将振子的质量、阻尼力和线性化处理后的表达式代入后,整理获得振子的振动方程为:
(7)
式(7)适用于振子1和振子2。
3 双磁悬浮振子结构仿真模型
有振动时,振子1的绝对位移为,
y1j=2l+y10+Δy1-Δx
(8)
有振动时,振子2的绝对位移为,
y2j=3l+y10+Δy1+y20+Δy2-Δx
(9)
分别代入振子运动方程,得到双磁悬浮振子仿真模型,见图3。

图3 双磁悬浮振子结构仿真模型
图3中,C1、C2、C3、C4为振子1和振子2所受磁排斥力表达式中分母的多项式系数,C5为多项式分子,C6为阻尼力比例系数,C7为振子的质量。图3上半部分为振子1的仿真部分,下半部分为振子2的仿真部分。x为输入振动信号,y2为输出信号。有振动产生时,振子1和振子2均等效受到与外加振动相反的加速度信号,即是测量系统的输入激振信号。振子2输出与被测振动信号幅值近似成比例,相位近似相反的输出信号。
外加图4所示振动信号,加速度频率是1 Hz,最大加速度0.01 m/s2。

图4 加速度输入波形
输出为振子1的相对位移,通过标定将该相对位移标定为加速度,得到外加振动振子1仿真加速度测量输出波形及功率谱,见图5。

图5 振子1输出波形
图5可见,仿真得到的振子1的振动加速度频率与外加振动相同,加速度幅值低于外加振动的加速度幅值。
同理,得到外加振动振子2仿真加速度测量输出波形及功率谱,见图6。

图6 振子2输出波形
图6可见,仿真得到的振子2的振动加速度频率和波形与外加振动相同。振子2的输出幅值高于振子1,测量灵敏度得到了提高。采用更多磁悬浮振子虽然可以进一步提高测量灵敏度,但提高幅度不大,且系统的阻尼力所占比重明显增加,对安装模型垂直度的要求也相应提高,所以,本系统采用双磁悬浮振子的结构设计。
4 地铁机车振动测量
对地铁机车振动进行测量:无振动时,有振动时和地铁站台的振动测量。见图7。

图7 地铁机车及站台振动波形
图7可见几种情况的振动波形不相同。图7(a)为机车匀速平稳运行时,测得垂直方向振动加速度波形较平坦,最大振动加速度幅值为0.048 m/s2,机车运行大部分时间是这种波形;图7(b)为机车匀速运行时部分路段出现振动,测得垂直方向最大振动加速度幅值为0.2 m/s2,其波形出现较为明显的波动;图7(c)为在地铁站台进行的振动测量,当地铁机车进站时,在站台测得垂直方向最大振动加速度幅值为0.1 m/s2,地铁机车进站时对站台产生一定的振动。
5 小波分解
为进一步获得不同状况下测量信号的特征,对测得的振动加速度信号采用多尺度一维小波分解函数,对振动信号进行分析。
图8为机车无振动一维尺度分解,机车无振动时,第3层的低频系数值为0.035 m/s2,第3、2、1层高频系数为0.048 m/s2,高频系数高于低频系数,第2层的低频系数值为0.035 m/s2,第2、1层高频系数为0.048 m/s2。2、1层高频系数较大,而低频分量不明显。低频分量小说明此段地铁轨道没有较大的起伏,平整度较好。

图8 机车无振动波形一维尺度分解
图9为机车匀速运动有振动一维尺度分解,机车有振动时,第3层的低频系数值为0.48 m/s2,第3、2、1层高频系数为0.15 m/s2,第2层的低频系数值为0.40 m/s2,第2、1层高频系数为0.15 m/s2。3、2、1层低频系数较大。机车起伏较大的原因是轨道平整度不够,需要对该地铁轨道路段进行重点检查,对可能与该频率产生共振的部件进行深入研究。

图9 机车有振动波形一维尺度分解
图10为在地铁进站时,在站台测得的振动信号一维尺度分解。

图10 地铁站台振动波形一维尺度分解
由图10可见当机车进站时对站台产生的振动信号中低频分量较高,与在机车匀速运动时有振动的情况类似,但幅值均小于机车上测得的信号数值。第3层的低频系数值为0.2 m/s2,第3、2、1层高频系数为0.1 m/s2,第2层的低频系数值为0.185 m/s2,第2、1层高频系数为0.1m/s2。3、2、1层低频系数较大。由于机车进站时有减速动作,由此会产生较大的振动,该值主要是由机车减速造成的,由此并无法判定站台附近的轨道情况,所以通过该信号小波分析无法判定轨道的情况。
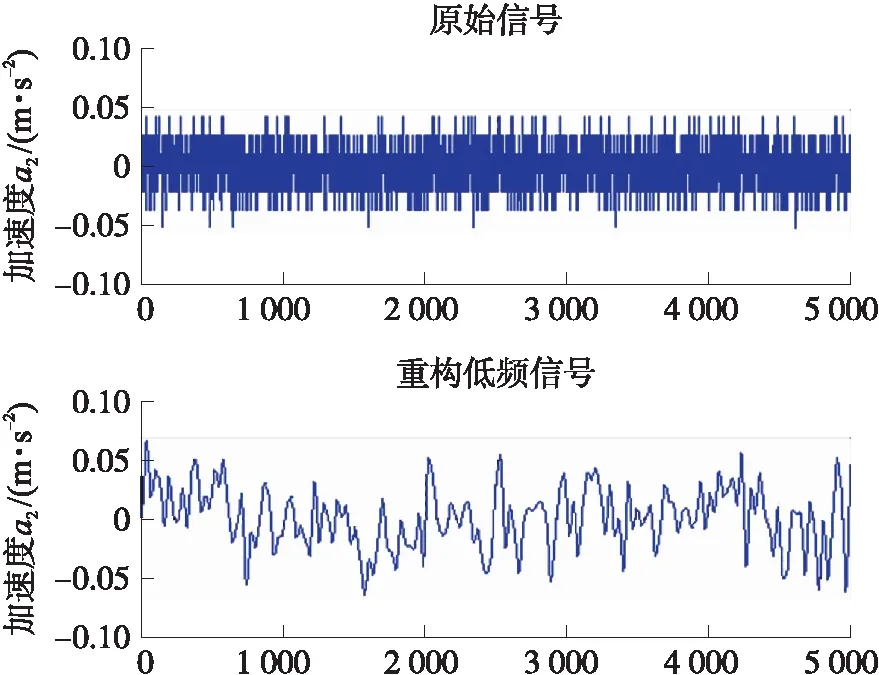
图11 机车无振动波形重构
6 小波重构
对小波分解可以了解振动信号高、低频频率分布情况。最终希望了解振动信号在不同时刻的振动特征。需要对几种情况振动波形进行重构。
图11为机车无振动时对测量波形进行的重构。由图11可见,垂直方向振动加速度幅值为0.048 m/s2,重构低频信号幅值在0.05 m/s2,幅值较小且频率分布均匀。说明机车的运行状况良好,此段地铁轨道较为平整。
图12为机车有振动时对测量波形进行重构的低频信号。由图12可见,有振动时其振动频率的幅值较大,不同区段出现了较为相同频率的振动,垂直方向振动加速度幅值为0.22 m/s2,重构低频信号幅值在0.22 m/s2左右。由此可以准确判断存在问题的地铁轨道的位置。进一步可通过模态分析等方法,分析出产生该振动频率的可能故障原因,并采取具有针对性的检查和维修。

图12 机车有振动波形重构
图13为地铁站台测量波形进行的重构的低频信号。由图13可见,机车在进站减速过程中,对站台产生了低频振动,其振动幅值也较大。垂直方向振动加速度幅值为0.12 m/s2,重构低频信号幅值在0.12 m/s2左右。且在前面部分的振动频率与在机车上测得的有振动频率相同。该振动可能是由于机车进站时有减速造成的,由此不能完全判定站台附近的轨道情况。对地铁站台附近轨道判定应当在非运期间,从地铁起点站和终点站全程匀速运行机车,运行中重点对站台附近的轨道工作状况进行检测。
7 结论
双磁悬浮振子结构可以提高测量灵敏度,其测量灵敏度高于单磁悬浮振子结构。该测量方法因振子处于悬浮状态,测量灵敏度较高,易于测量低频振动加速度信号,适合于对地铁机车和地铁站台等的振动测量。通过地铁机车运行中的振动判定地铁轨道是否工作正常,并判定可能存在的故障路段。通过小波分解和振动波形重构可以很方便的区分不同的振动,在匀速运行过程,通过有振动的波形对轨道可能出现问题的区段进行准确定位,对站台附近的轨道检测需要在夜晚停运期间,全程匀速运行机车,实现对站台附近的轨道故障检测。通过获得的有振动波形频率特征,通过模态分析等方法对照研究,可实现更进一步的故障原因查找和定位。磁悬浮振动测量对于需要较高测量灵敏度的绝对式振动测量具有较明显的优势。
