基于核方法协同表示的高光谱图像分类

刘遵雄，蒋中慧，任行乐

(华东交通大学 信息工程学院, 江西 南昌 330013)

0 引言

高光谱图像是利用遥感传感器在高空中获取地面物质电磁波波段的特性得到的遥感图像，相比于传统的光学遥感传感器，高光谱传感器检测到的波段范围更加广泛，不仅仅覆盖人体肉眼可见的可见光部分，还包括红外和紫外波段部分。不同的地面物质有不同的电磁波反射特征，通过利用不同地物具有不同反射的特性可以完成对高光谱图像数据的分类[1]。例如在城市地物、海洋生态、环境污染、农业检测等等领域都有着重要的作用。

为了利用高光谱图像的光谱特征完成分类，很多分类方法被提出，例如随机森林(random forest)方法[2]，支持向量机(support vector machine,SVM)方法[3-4]。相同物质的像元在用训练样本对其线性表示时，表示系数是相近的。为了利用该相似特性，基于稀疏表示的分类算法(sparse representation classification,SRC)[5-6]越来越多的被用于高光谱图像数据的分类，通过训练样本的稀疏线性组合来重构一个测试像元，然后通过计算最小重构误差作为依据完成分类。由于高光谱图像数据量大、维度高，对图像信息的稀疏表示显得尤为重要，同时稀疏表示可以有效获取高光谱图像数据的特征，具有良好的分类效果。

本文基于稀疏表示的分类思想，以及将数据投影到高维特征空间再完成表示过程可以提高不同类别数据可分性的效果，提出了基于核方法协同表示与绝对距离融合的分类方法。主要思想在于利用核函数完成数据的非线性映射后，在特征空间中用全部训练样本表示待测样本，利用表示向量来计算重构残差值和各类样本对待测样本的表示向量，进而确定待测样本的分类标签。

1 相关工作

文献[7]中对Y进行稀疏编码表示:y≈θα,其中θ是一个过完备的字典，α是一个稀疏向量，且α的稀疏性由L1范数来表示，那么稀疏模型就可以表示为：

(α)=arg min ‖α‖1s.t. ‖y-Xα‖2≤ε。

(1)

假设有n个已知类别的训练样本数据X,Xi∈Rd(d是特征的维数)，n个样本属于不同的类别ωi{i=1,2,…,C}(C是类别的数量)，所有类别的样本数量求和为n。当有一个测试样本数据出现时，使用不同类别数据通过范数L1正则化对测试数据稀疏程度进行控制，稀疏表示模型表示为：

(2)

λ1是用于控制稀疏向量α的正则化参数，α可以通过多种算法完成计算，比如基追踪(BP)算法[8],正交匹配追踪(OMP)算法[9]等，计算出系数后再对各表示系数计算残差r(y)：

r(SR)(y)=‖y-Xα(SR)‖2。

(3)

X可以从训练样本中获得，通过计算可知哪个类别的表示系数可以得到更小的重构误差，那么就可以确定待测像元类别。

为了利用数据中类别之间的协同关系，对SRC算法改进的协同表示分类算法(collaborative representation classification，CRC)[10-12]被提出，文献[13]中指出CRC这种基于协同表示的分类算法是强调所有的样本共同表示单个像元，而不再是仅仅利用稀疏性。由于高光谱图像的成像机制带来的维数问题,在一定程度上给分类带来挑战，文献[14]提出基于核方法投影数据的稀疏表示分类算法(kernel sparse representation classification,KSRC)，通过使用内核技术优化原算法，再使用获得的稀疏表示向量来确定待测像素的类标签。

2 本文研究方法

2.1 协同表示正则化方法(CRT)

SRC算法用于高光谱图像分类时强调了稀疏性对于分类的重要性，自动选择去掉一些不包含信息的特征，达到减小误差的目的。但是这种思想没有充分利用图像中不同类别像元之间的相似性，这种相似性有助于进行分类。为了突出样本之间的协同性质，对稀疏表示算法进行改进就有了协同表示分类算法，假设X=[X1,X2,…,XC]∈Imxn，测试样本Y∈Im，那么Y就可以被表示为：

y=a1x1+a2x2+…+anxn。

(4)

协同表示分类算法用所有的训练样本来协同表示测试样本，并使用正则化的最小二乘法,那么CRC[15]方法的模型可以表示为：

(5)

λ是用于控制向量α的正则化参数，使用范数L2对α进行约束，可以使α的每个元素都很小接近于0，但和范数L1不同的是，不会令其为0，可以充分利用所有训练样本的表示能力，也实现了对模型空间的限制，一定程度上避免了过拟合，提高模型的泛化能力，同时范数L2相比于范数L1更有助于处理矩阵求逆困难的问题，让优化求解的过程更加稳定和快速。本文使用范数L2正则化项可以使最小二乘解更稳定，同时比范数L1使用稀疏性效果更好。CRC算法的解析解表示为：

α(CRC)=(XTX+λI)-1XTy。

(6)

X可以从训练样本中获得，通过计算可知哪个类别的重构残差更小，那么就可以确定测试像素类别。残差值的计算公式为：

(7)

(8)

其中Γy为正则化矩阵，它是一个对角线矩阵，对角线上的元素为所有的训练样本数据和测试样本数据的距离,Γy表示为：

(9)

其中X1，X2,…,Xn为训练样本数据，如果某个距离值越小，那么说明相应的数据类别和测试数据类别越接近。CRT算法的解析解表示为：

(10)

CRT判断测试数据类别的方式与CRC相同，通过计算重构误差判断测试数据类别。

2.2 核方法

核方法[16-18]的作用是可以创造出一个隐式非线性的映射机制，将在低维空间中线性不可分的点集映射到高维空间中完成线性可分的过程，非线性的隐射机制过程可以表达为：

y∈Rd→φ(y)=[φ1(y),…,φs(y)]∈Rs。

(11)

φ(y)由y通过高维特征向量隐射得到，且s远远大于d。如果将两个点集隐射到高维空间中，那么俩映射向量的内积就是原低维空间中两点集之间的核函数，其核函数的可以表示为：

k(yi,yj)=φ(yi)Tφ(yj)。

(12)

常用的核函数有线性核函数，多项式核函数以及高斯核函数，在本文实验过程中使用的核函数为高斯核(gaussian kernel)函数，也被称为径向基核函数。这种核函数对数据中的噪音有着良好的抗干扰能力，在实验中经过多次尝试找到最佳的核参数可以使核函数有更好的性能。高斯核函数的数学形式表达如下：

(13)

通过这种非线性的映射机制，将原有训练样本的所有数据映射到高维空间中进行模型学习，即φ={φ(x1),φ(x2),…,φ(xn)}∈Rs×n, 测试样本可以表示为Φ的线性组合为φ(y)=φα。

2.3 Abs_KCRT

本文提出了一种基于核方法协同表示与绝对距离融合的分类算法(Abs_KCRT)。首先利用核技术完成数据投影，用特征空间中所有训练样本表示待测样本，通过表示向量来计算待测样本的重构残差向量，其次将不同类别内所有样本对待测样本表示系数值绝对值求和作为影响因子，再与基于表示的算法计算得到的残差予以不同权重进行融合，最后将融合后的残差值作为新的分类依据，完成高光谱图像分类。其中KCRT的求解模型可以表述为：

(14)

其中ΓΦ(y)是新的吉洪诺夫对角线矩阵，对角线上的元素为所有映射到高维空间的后训练样本数据和测试样本数据的距离，ΓΦ(y)表示为：

(15)

其中φ(y)与φ(Xn)是y与x映射到高维空间的结果，‖φ(y)-φ(xi)‖2=[k(y,y)+k(xi,xi)-2k(y,xi)]1/2,i=1,2,…,n。解得KCRT的封闭解为：

(16)

其中K=φTφ∈Rn×n是Kij=k(xi,xj)的格拉姆矩阵。

协同表示是用所有类的样本来完成对测试样本线性组合的过程，而不再是利用稀疏性，训练样本各类别表示系数向量元素绝对值求和，表现了在所有类别中该类对测试样本表示的总贡献度，由此来表达测试样本与每个类别的相似度，值越大那么可以认为测试样本与相应的类中样本相似度越高,训练样本表示向量绝对值求和分类模型(ABS)表述为：

Class(y)ABS=arg max{di}，di=∑|ai|。

(17)

算法充分利用了不同类别样本对测试样本的协同表示，不仅利用测试样本的重构误差来判断图像类别，以及不同类别样本对测试样本线性表示时的贡献度来判断。实验证明这两种判断依据均可以作为分类依据。前者通过得到各类协同表示系数后计算重构误差，由最小残差对应的类别来确定测试样本类别，后者先计算每个类别内所有样本对测试样本的表示系数向量元素取绝对值再求和，由于某一类别各样本表示系数绝对值求和的值越大和训练样本重构残差的值越小均表示测试样本与该类别相似度越高，所以为了更好的提升图像信息的分类效果，本文将每个类别所有样本表示系数取绝对值求和再予以不同权重作为重构误差的影响因子，使两种分类依据同时起作用，算法分类依据模型表述为：

RAbs_KCRT=α(KCRT)-kdi。

(18)

新得到的残差不仅仅包括测试样本的重构误差还包括各样本所有训练数据对测试样本类别投票值，k的值不同则影响因子的影响程度也不同。最终通过Abs_KCRT计算出如下所示的重构残差与绝对距离融合值来分类测试像元y为：

(19)

对CRT框架改进的基于核函数协同表示与绝对距离融合分类算法的具体流程总结如算法1所示：

Step1:选择核函数,通过实验确定合适的核参数。

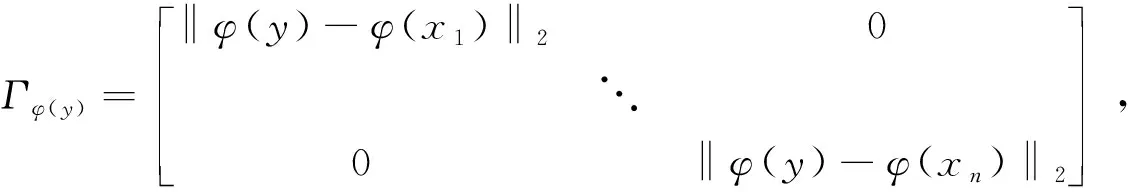
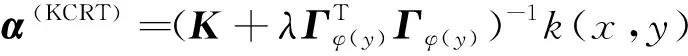
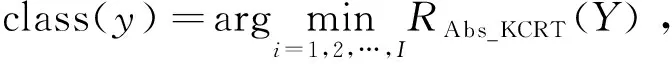
Step5:返回下一个待测像元，完成计算分类过程。

3 结果和讨论

为了验证本文算法的有效性，实验采用CRC,KCRT,ABS, SVM以及本文的算法Abs_KCRT对两种不同的高光谱数据集进行了实验分析和对比，为更好比较，支持向量机实验中采用与本文算法中相同的核函数，即径向基函数(RBF)，输入灰度共生矩阵的纹理特征向量包括相关性，对比度，同质性和二阶矩。在实验前对数据进行平滑处理，对于每一类有标记的样本，实验过程每次选取10 %、20 %、30 %作为训练样本，剩下的样本作为测试样本，每组实验均运行10次对结果取平均值。实验使用了三种评价准则：

① OA,总体精度，即正确分类样本数比总样本数;

② AA，平均精度，即每类分类结果的平均值;

③ Kappa，一致性检验。

在本文中提出的基于核方法与绝对距离融合的协同表示算法需要通过多次实验完成调参过程以获得最佳超参数。第一个是算法中正则化项的控制参数λ，λ值大小控制着协同表示中正则化项的重要程度，良好的正则化项可以预防出现过拟合现象。第二个是协同表示计算残差与绝对值距离向量的融合系数k，其值大小控制着影响因子对表示残差的作用程度，不同参数下精度统计曲线见图1。通过多次实验发现，当λ值取0.001时，正则化项的作用最好；随着k值的增大，分类精度先增大再减小，在k取0.1时，分类效果最佳。

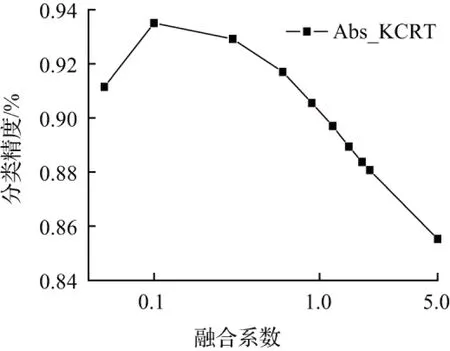
(a)不同融合系数下本文算法精度统计曲线

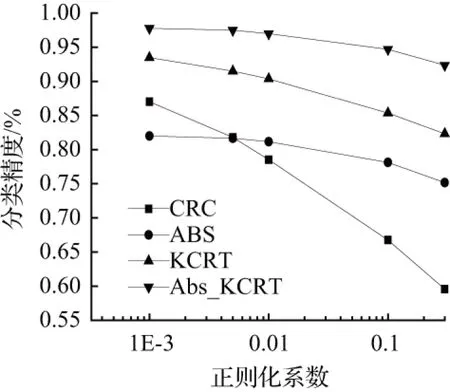
(b)不同正则化系数下各算法精度统计曲线

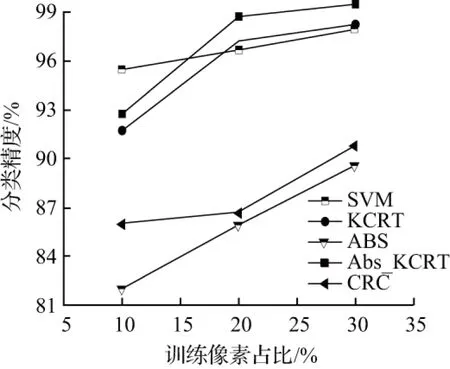
图2 Indian Pines训练集数量对各算法分类精度影响

3.1 Indian Pines数据集实验分析

第一个用于实验的高光谱数据集是 Indian Pines，该高光谱影像是由AVIRIS传感器采集而成的印度松树测试地，该影像具有145×145个像元，包含了16种类别的地物，空间分辨率为20 m，并拥有220个波段，覆盖了波长从0.4～2.5 μm的光谱信息。除去20个含噪声波段，将剩余的200个波段作为研究对象。实验中的参数通过交叉验证得到λ=0.001，k=0.1。表1列出了Indian Pines数据集中样本类别及其数目，表2为Indian Pines数据集5种算法的分类结果。图2为Indian Pines中不同训练集数量对分类精度的影响。

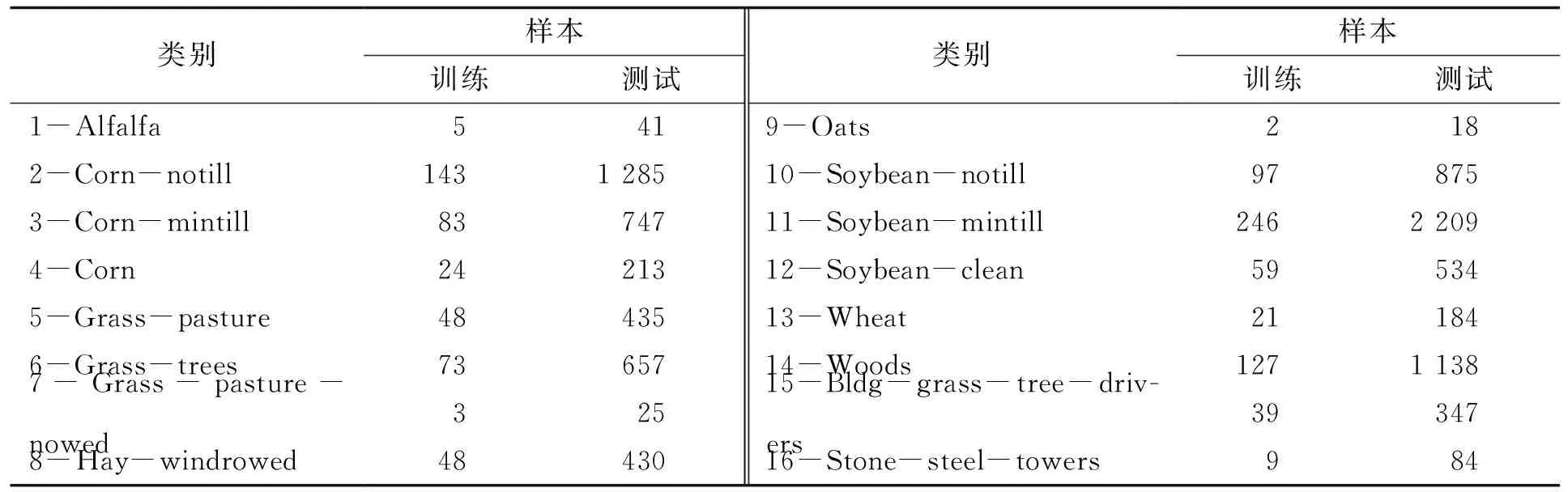
表1 Indian Pines数据集中样本类别及其数目

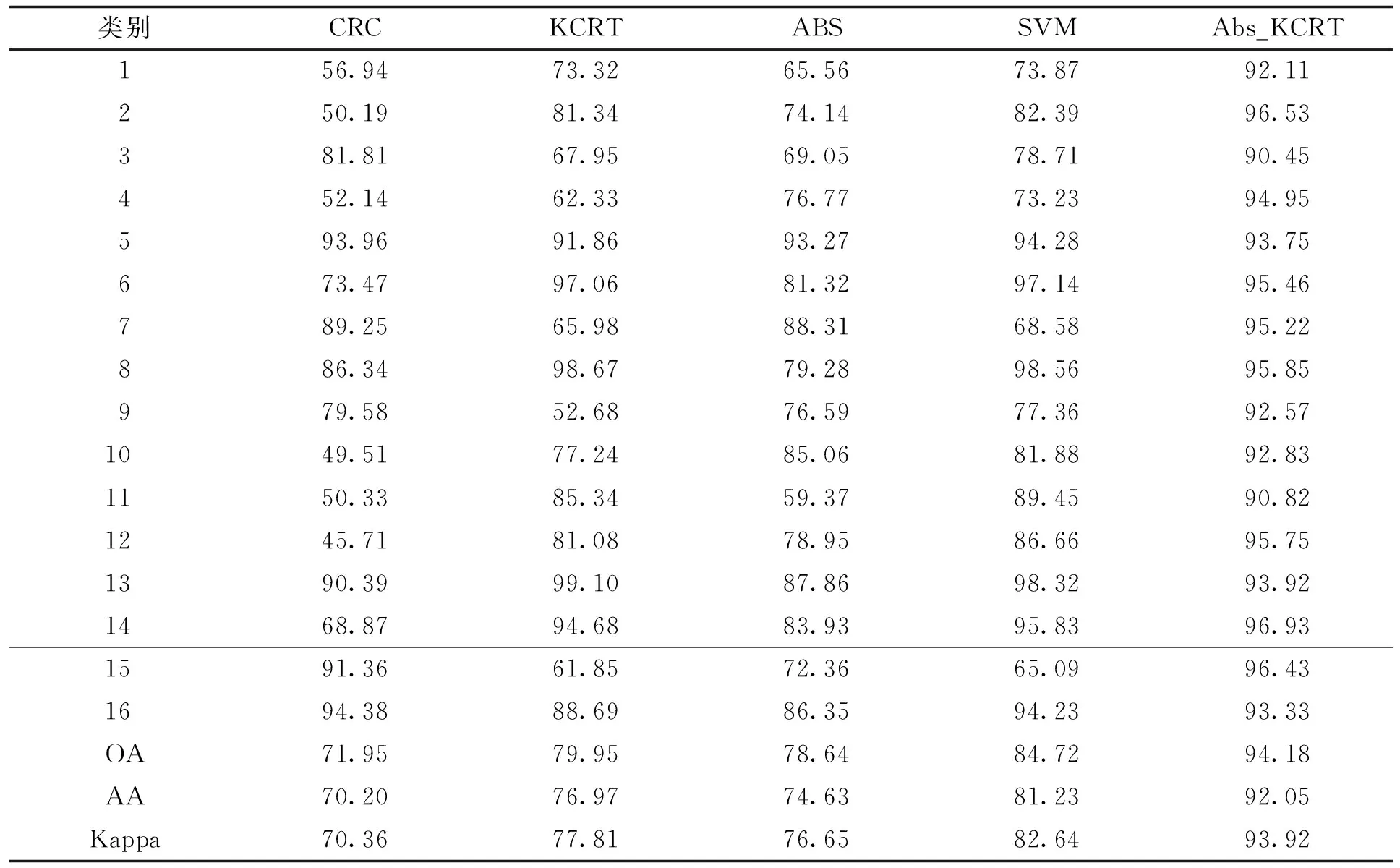
表2 Indian Pines数据集上的分类精度

由表2中在Indian Pines上使用本文提出算法和一些对比算法的分类效果可知，传统的协同表示方法对图像中地物分类时，精度较低且鲁棒性不佳，本文算法在总体分类精度、平均分类精度和Kappa系数均有所提高，与SVM方法相比，分别提高了9.46 %、10.82 %、11.28 %。与KCRT方法相比，分别提高了14.23 %、15.08 %、16.11 %，特别在(1-Atfalfa)、(4-Corn)、(15-Bldg-grass-tree-drivers)这三类精度较低的地物类别分类得到了较为显著的提升，分类精度提高了18.79 %、22.62 %、34.58 %，实验结果说明本文方法对易分类错误的地物具有较好的分类效果，其良好的鲁棒性可以有效提升总体分类精度。

3.2 Pavia University数据集实验分析

第二个用于实验的高光谱数据集是Pavia University，该高光谱影像是由ROSIS于2003年采集的意大利帕维亚大学的场景，图像有610×340个像元，包含了9种类别的地物，空间分别率为1.3 m,包含了115个光谱波段,去除12个噪声波段，将剩余的103个波段作为研究对象。表3列出了该数据集内9个类别对应名称及实验中使用的测试样本和训练样本数量，图3为Pavia University训练集不同数量对分类精度影响，表4为Pavia University数据集4种算法的分类结果。

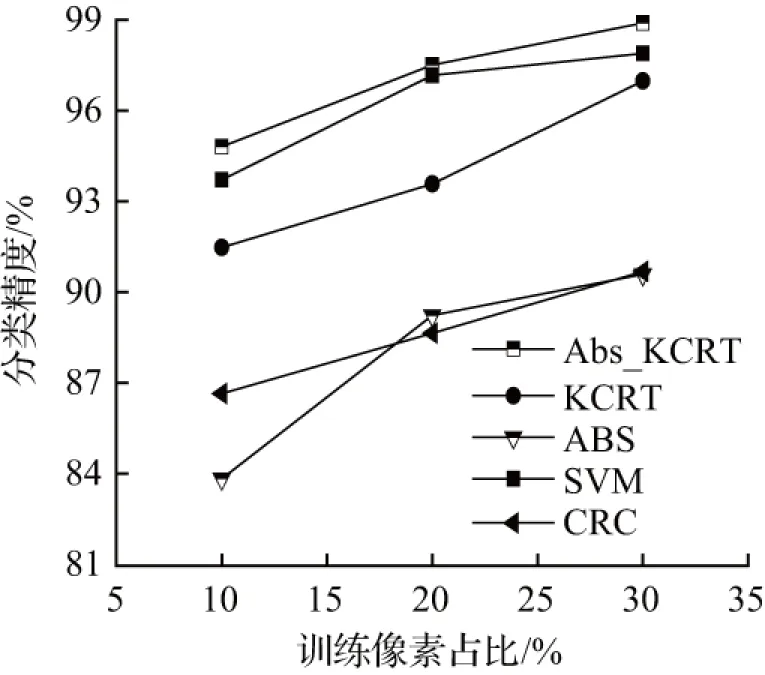
图3 Pavia University训练集数量对各算法分类精度影响

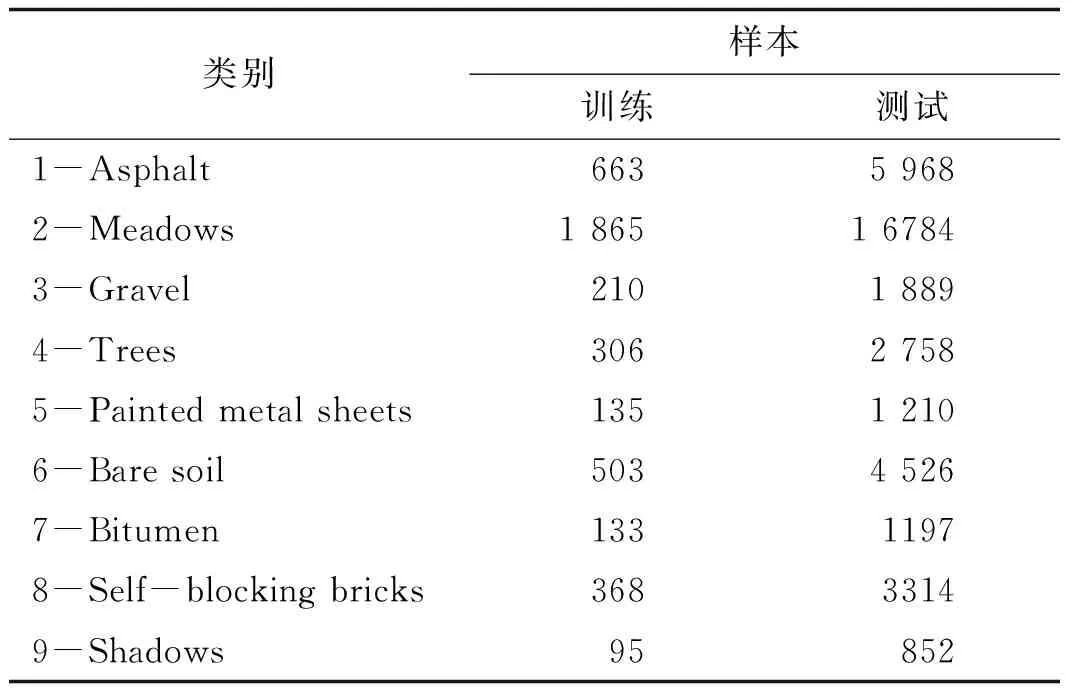
表3 Pavia University中样本类别及其数目

由表4中在Pavia University上使用本文算法和一些对比算法的分类效果可以看出,在绝大多数类别中，本文提出算法较其他算法在总体分类精度和平均分类精度上有一定的提高。但是需要注意的是Pavia University的数据集较大，且包含很多大小不均匀且复杂的区域结构，基于表示的算法实现较慢，所以在实验中协同表示的时间较长。通过在帕维亚大学高光谱实验数据集上的实验结果可以看出，本文算法在总体分类精度、平均分类精度和Kappa系数均有所提高。与SVM方法相比，分别提高了8.07 %、11.26 %、11 %，与KCRT方法相比，分别提高了12.12 %、13.65 %、12.59 %，特别在(3-Gravel)、(6-Bare soil)、(7-Bitumen )这三类精度较低的地物类别得到了较大改善，单类别分类精度提高了22.2 %、26.41 %、22.62 %。

图4为四种基于表示方法分类时间对比，为了方便比较，将CRC算法分类时间设为1，CRC算法在Indian Pines数据集上分类时间为18.48 s，在Pavia University数据集上分类时间为70.54 s。使用了核方法完成非线性映射再完成分类，算法的时间复杂度有一定程度的增加，但是Abs_KCRT算法在两种经典高光谱图像数据集上均取得了较为明显的分类精度提升。说明本文方法对协同表示方法采用核方法和绝对距离融合改进的策略实现了提升总体分类精度的目标，并在两组实验中都取得了优于SVM和传统算法CRC的总体分类精度，稳定处于最佳表现状态。

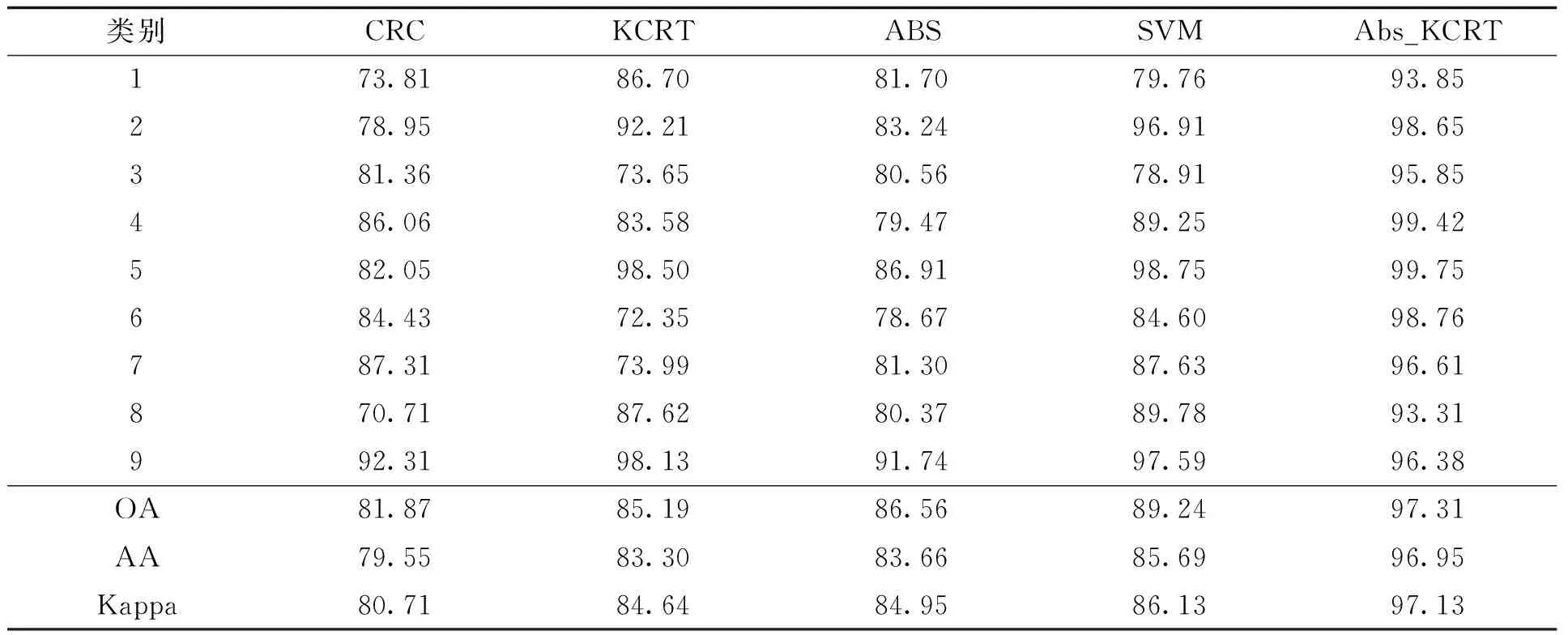
表4 Pavia University数据集上的分类精度

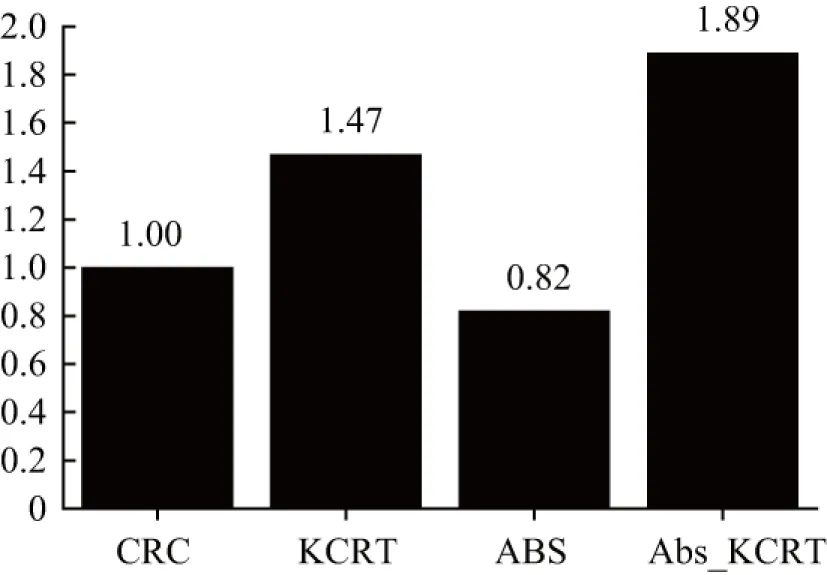
(a)Indian Pines数据集上分类时间比较

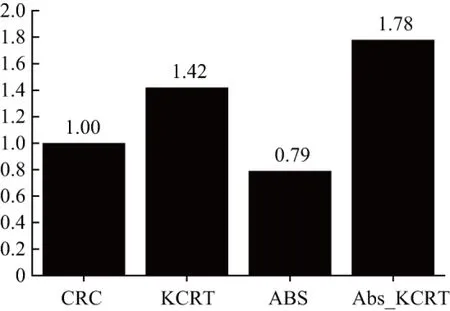
(b)Pavia University数据集上分类时间比较

图4 4种基于表示方法分类时间对比

Fig.4 Comparison of classification speeds of four method based on representation

4 结语

本文提出一种基于核方法协同表示融合的分类算法来完成高光谱图像中地物分类，对传统协同表示方法进行改进的创新点通过两种高光谱数据进行实验验证，通过多次实验仿真得到良好正则化系数，核参数和融合参数的值，取得较好分类效果。实验结果表明：①利用核方法完成数据投影，以及增加训练样本规模，会使得完成分类的速度有所下降，但可以带来明显的分类精度提升；②本文算法在高光谱图像数据集不同种类地物上的分类精度提升有所不同，但均优于传统的协同表示方法及SVM的分类结果。后续研究工作需通过优化表示的过程，加入矩阵低秩策略对数据处理加以改进，在提高算法分类效果的同时降低分类过程的时间复杂度。