带裂纹简支梁中性轴偏移规律分析

刘文祥 曾欢艳 梅华

【摘 要】工程实际中梁类构件通常带裂纹服役，通过对带裂纹简支梁进行有限元分析，得到裂纹梁的中性轴偏移规律。裂纹对中性轴的干扰集中在距离裂纹面一倍截面高度范围内，符合圣维南原理。在裂纹远场区，中性轴与形心轴重合，在裂纹近场区域中性轴呈M形，其值主要受相对裂纹高度c/h和距离裂纹面的相对长度x/h控制，论文同时给出了中性轴的拟合表达式。

【Abstract】 Beams always served with cracks in engineering structure， based on the finite element analysis of cracked beam， the neutral axis migration law of cracked beam are obtained. Interference of crack on the neutral axis is concentrated in the range of one section height from crack surface， which conforms to the Saint Venant's principle. In the far region of the crack， the neutral axis and the centroid axis reunite， in the crack near field， neutral axis shaped as M， and its value is mainly controlled by relative crack height c/h and relative distance x/h from the crack surface. At the same time， the fitting expression of neutral axis is given.

【关键词】裂纹梁;中性轴;偏移规律

【Keywords】 cracked beam; neutral axis; migration law

【中图分类号】TU323.3                                            【文献标志码】A                                【文章编号】1673-1069（2019）09-0194-03

1 引言

梁、柱是工程结构中常见的结构构件，计算分析时通常采用梁单元模拟。结构模型内力分析以材料力学和结构力学基本理论为基础，认为梁单元横截面应力呈线性分布，对于均质构件，截面的形心轴、中性轴重合。而工程实际中，梁、柱类构件通常是带裂纹服役的，裂纹产生后，首先导致构件横截面有效面积减少，中性轴往开裂方向移动，进而导致截面惯性矩减少，柔度增大，因此，分析带裂纹梁的中性轴偏移规律具有一定意义。在梁中性轴位置上研究历史较久[1]，最早由Galileo开展，近来，黄良[2]对纯弯曲损伤梁的中性轴偏移规律进行了研究，得出中性轴位置与截面系数、损伤模量之间的关系，陈祖明[3]推导了纯弯曲屈曲梁后中性轴的位臵公式和应力分布公式。吴晓[4]研究认为轴向力作用下梁弯曲时的中性轴位置偏移距离非常小。王长钟[5]采用有限单元柔度法，对构件截面刚度变化后的中性轴偏移与转动进行了分析。本文在前述研究的基础上，采用ANSYS有限元软件分析了受均布荷载带裂纹简支梁的中性轴偏移规律，并给出其拟合表达式。

2 裂纹梁分析模型

如图1所示简支梁，截面尺寸b×h=0.2 m×0.4 m，跨度l=4.8m，建立图示坐标系，梁上受均布线荷载q=5 kN/m，材料弹性模量E=3.0×104MPa，泊松比μ=0.2，跨中裂纹长度为c。可以将简支梁简化为平面应力分析模型，网格离散情况如图1所示，单元边长20mm，裂尖奇异区域采用4个1/4节点奇异单元模拟。现利用ANSYS軟件中Plane82单元分析简支梁中性轴偏移规律。

3 中性轴偏移规律

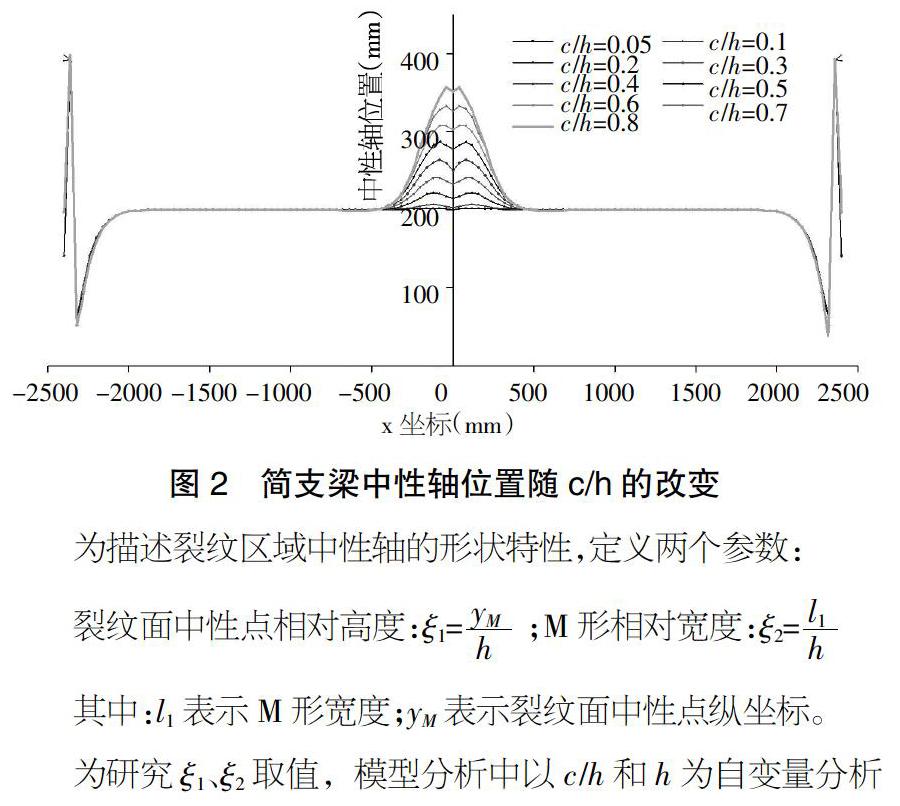
在ANSYS中以横截面为路径提取应力，取路径上应力绝对值最小的点为中性点，连接中性点得到梁的中性轴。当c/h变化时，简支梁的中性轴形状变化如图2所示，梁端由于支座约束位置与理想状态中约束在形心轴处不符，距离梁端一个截面高度范围内中性轴位置不准确。裂纹区域中性轴呈M形，由裂纹面向两端，中性轴位置先增大，出现极大值，然后减小，一直减小到形心轴以下稍许后再恢复与形心轴重合，随着c/h增大，裂纹区域中性轴位置上移，且上移幅度变大。

从表1列出的M形ξ1值可知，尽管简支梁的截面高度不同，但c/h相同时，裂纹面中性点相对高度ξ1相同。该结论也可证明中性轴的变化与跨长无关，如由h=0.4 m变换到h=0.6m后，可视为将4.8m简支梁尺寸放大了1.5倍，而跨长足够大时不影响中性轴分布，所以可将放大后的尺寸减去2.4m得到h=0.6m时的分析模型，因此，改变截面高度相当于所有量都放大了相应倍数，而ξ1的值不变。

表1给出的M形相对宽度ξ2表明，在c/h较大时，同一c/h下ξ2基本相同，c/h较小时ξ2差别较大，且随跨高比减小而增大，不同截面高度下趋势线变化规律一致。当c/h=0.5时达到最大值，c/h<0.5时为增函数，c/h>0.5时为减函数，但递减趋势不明显。随着相对裂纹长度的增大，M形变宽，当c/h达到0.5后，相对裂纹长度增大，不会造成M形变宽，而是使M形变高。

图3、图4给出了不同梁高、不同裂纹长度下的ξ1、ξ2取值变化规律，梁高不同时ξ1与c/h呈线性关系，ξ2与c/h呈非线性关系，以c/h为自变量，利用Matlab做拟合，可得：

通过分析不同截面高度、不同荷载工况下裂纹区域的中性轴形状，裂纹影响区域内中性轴的位置主要与c/h、x/h相关，通过拟合可以得到裂纹区域中性轴Y的通用表达式：

4 结论

本文对受均布荷载的带裂纹简支梁进行分析，得出简支梁的中性轴偏移规律以及裂纹区域中性轴的表达式。中性轴在裂纹远场区与形心轴重合，在裂纹区域呈M形，其相对宽度主要受相对裂纹高度影响，裂尖中性点位置与相对裂纹高度存在线性关系。

【参考文献】

【1】老亮.梁中性轴简史试编[J].力学与实践，1986（04）：60-62.

【2】黄良，李相麟.矩形梁纯弯曲损伤时的中性轴偏离[J].南昌大学学报（工科版），2002（02）：59-61.

【3】陈祖明.纯弯曲梁屈服后中性轴位置分析[A].北京力学会.北京力学会第二十三届学术年会会议论文集[C].北京力学会：北京力学会，2017：2.

【4】吴晓，李叶林.关于轴向力作用下梁弯曲时中性轴位置的讨论[J].工程与试验，2018，58（03）：1-2+124.

【5】王长钟，王鑫.钢筋混凝土梁柱中性轴偏移现象的柔度法分析[J].江苏建筑，2010（01）：77-79.