不同轴压比钢管混凝土边缘约束叠合剪力墙的抗震性能
2019-11-26侯和涛颜雪雪程积润王彦明方明霁李明俊
侯和涛 颜雪雪 程积润 王彦明 方明霁 李明俊


摘 要:对1片现浇剪力墙和轴压比不同的3片新型钢管混凝土边缘约束叠合剪力墙进行拟静力试验,研究其在往复水平荷载作用下的试验现象、破坏形式和抗震性能,提出钢管混凝土边缘约束叠合剪力墙屈服承载力的计算方法;采用XTRACT有限元分析软件对新型剪力墙峰值承载力进行算例验证,二者结果吻合较好。研究表明:钢管混凝土边缘约束叠合剪力墙的水平承载力和耗能能力较现浇混凝土剪力墙有所提高;其承载力随着轴压比的增大而增大;实验范围内的轴压比对其耗能能力的影响较小。
关键词:钢管混凝土;叠合剪力墙;轴压比;承载力;抗震性能
中图分类号:TU375 文献标志码:A 文章编号:2096-6717(2019)05-0073-09
Abstract:Cyclic tests were carried out on a conventionally reinforced concrete shear wall and three sandwich shear walls with concrete filled steel tubes (SW-CFT). The vertical compression forces on the experimental specimens were varied. The failure mode and hysteretic behavior of each experimental specimen under the combined vertical compression and lateral cyclic loading were evaluated. The equations to calculate the wall lateral resistances associated with the yielding states were derived. The experimental specimens were also simulated by the computer program-XTRACT. Comparisons revealed that the derived equations and the computer model both provide reasonable predictions for the wall resistances. The result show that the SW-CFTs exhibited high horizontal bearing capacity and energy consumption. In addition, the axial compression ratio is proportional to the strength exaltation and has only marginal effects on the seismic behavior of the SW-CFTs within the test range in this study.
Keywords:concrete filled steel tube; sandwich shear wall; axial compression ratio; bearing capacity; seismic behavior
隨着装配式建筑的快速发展,预制叠合剪力墙得到了越来越广泛的运用。钢混剪力墙是目前应用较多的一种叠合剪力墙,主要有钢骨混凝土剪力墙、钢框架预制剪力墙、预制钢板剪力墙以及带有边缘约束构件的预制剪力墙4种形式。Thomsen等[1]、Kent等[2]、Humar等[3]指出,剪力墙在不同强度的地震作用下,结构的变形能力应大于结构的变形需求。马恺泽等[4-5]通过对型钢混凝土剪力墙的抗震研究,推导了其变形能力设计方法;连星等[6-7]对叠合板式剪力墙进行实验探究,提出了恢复力模型特征参数计算方法;钱稼如等[8-9]对钢骨、钢管混凝土剪力墙在高轴压比下的抗震性能进行研究,发现约束构件对提高墙体的延性有突出贡献,并提出了其承载力与位移的计算方法;侯和涛等[10]对钢管混凝土边缘约束叠合剪力墙的高厚比参数进行了拟静力试验研究,结果表明,该剪力墙具有较好的抗震性能;王滋军等[11-12]对新型剪力墙和约束边缘构件预制叠合剪力墙的抗震性能进行研究,解决了新老混凝土结合面的问题,实现了“等同现浇”;其他学者关于混凝土剪力墙的抗震设计研究也得出了大量的结论[13-15]。目前,对钢管混凝土边缘约束叠合剪力墙的研究较少,其性能有待深入研究。控制轴压比能够较好地控制结构的延性,因此,试验以轴压比为研究参数,探究其对钢管混凝土边缘约束叠合剪力墙(SW-CFT)力学性能的影响。
1 试验概况
1.1 试件设计
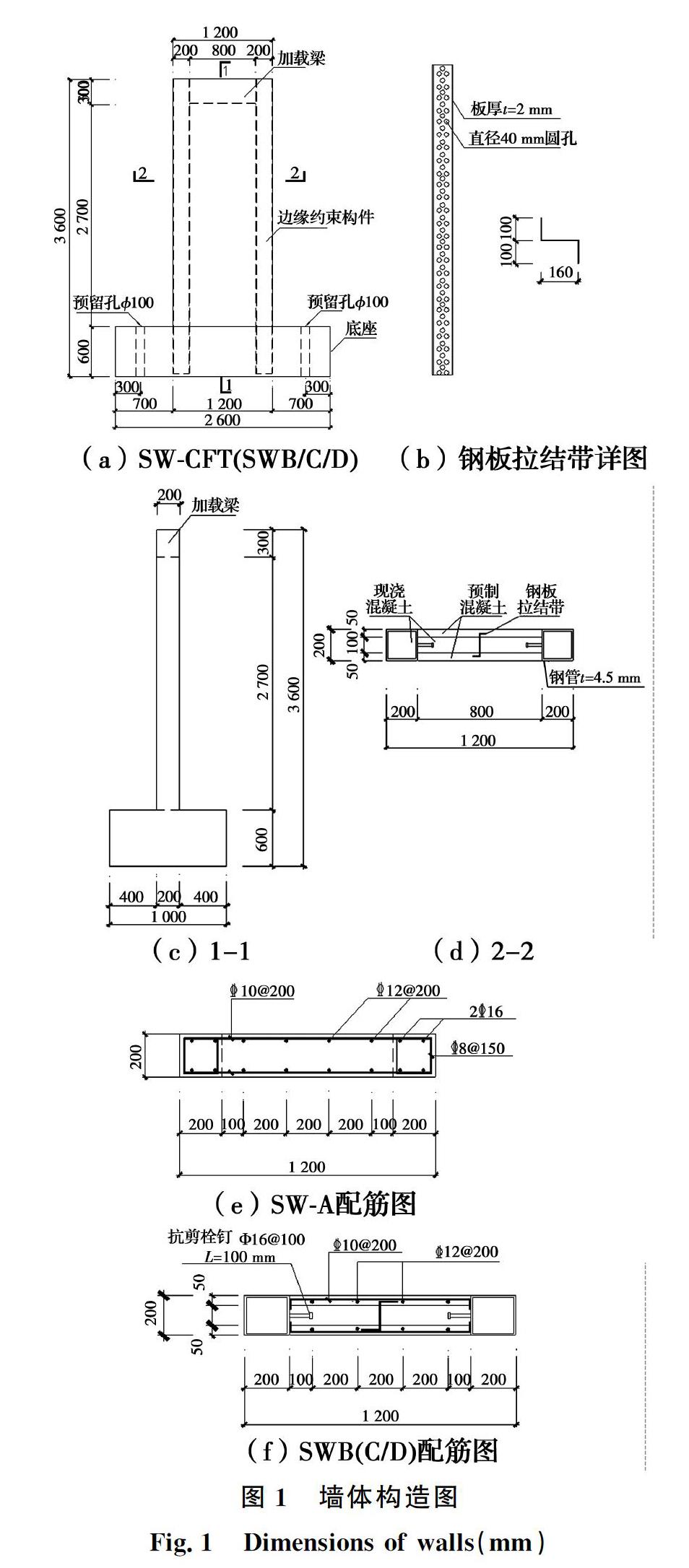
实验设计了4个试件,SW-A为现浇剪力墙,SW(B/C/D)为钢管混凝土边缘约束叠合剪力墙。SW-CFT墙由两侧的预制墙板和中间的空腔组成,两侧的预制墙板与钢管在工厂预制,运抵现场安装固定后,在两侧墙板的空腔和钢管内浇注混凝土。SW-CFT墙的竖向钢筋采用搭接连接,水平钢筋焊接在钢管上。在SW-CFT墙中间位置沿墙体高度设置钢板拉结带,以增强两侧预制墙板之间的拉结,为了减轻自重及增强混凝土的整体性,拉结带上设置若干圆孔。试验中SW-B/C/D轴压比分别为0、0.15、0.28,SW-A的轴压比为0.15。试件高度×宽度×截面厚度=3 000 mm×1 200 mm×200 mm,SW-CFT墙的配筋相同,墙体构造如图1所示,混凝土和钢材的材料性能指标见表1。
1.2 加载方案
试验采用位移控制加载,预加载结束后,竖向加载至预定的轴向压力后保持恒定,通过水平作动器施加水平荷载以实现加载历程。定义层间位移角为试件的顶点位移(D)与净高度(H=2 800 mm)的比值,根据GB 50011—2010[16]、GB 50010—2010[17]和《日本建筑基准法》(2002)[18],确定了如表2所示的加载历程,表中加载位移角从小到大依次为预加载、剪力墙结构弹性层间位移角、框架结构弹性层间位移角、日本抗震设计第一水准层间位移角、剪力墙结构弹塑性层间位移角、框架结构弹塑性层间位移角、文献参考值。试验加载装置如图2所示。
各试件的轴压比按式(1)计算。n=NAc·fc+Acc·fcc+Aa·fa
(1)式中:fc和fcc分别为现浇混凝土和预制混凝土的轴心抗压强度实测值,其值为0.76fcu,fcu为混凝土立方体抗压强度实测值;Ac和Acc分别为剪力墙横截面现浇和预制混凝土部分对应的面积;fa为试件竖向钢管的实测屈服强度;Aa为柱端竖向钢管横截面面积。
1.3 位移测点布置
试件共布置6个位移计,D1和D2测量墙体水平方向位移,D3和D4消除底座滑移的影响,D5和D6监控地梁是否转动。测点布置见图3。
2 试验现象及破坏模式
SW-A试件的裂缝主要集中在剪力墙1/2高度以下,裂缝出现较早,当位移角为1/610时,距底座约300 mm处的端柱产生第1条裂缝;荷载增加,裂缝变宽,数量变多,并逐渐向墙体中间扩展;当试件的承载力小于峰值荷载的85%时,剪力墙底部两端的混凝土被压碎,钢筋被压弯且外露于混凝土,加载结束,剪力墙主要破坏模式为弯曲型破坏。
3片SW-CFT剪力墙试件的裂缝发展及破坏模式相似,整个墙体上产生了均匀分布的裂缝,与SW-A试件相比,裂缝出现得较晚。以SW-C试件为例,初始加载时,墙体无可视裂缝;当位移角达到1/400时,剪力墙底部出现第1条水平裂缝;随后裂缝逐渐增多,分布区域也逐渐扩大,当位移角为1/190时,SW-C受压侧钢柱屈服,裂缝变宽,剪力墙底部形成塑性铰区;当位移角为1/120时,受压侧方钢管距墙底70 mm處出现鼓曲;加载后期,当位移角达到1/50时,距墙底150 mm的钢管处出现鼓曲,墙内竖向钢板拉结带的外侧混凝土逐步剥落,这是由于墙体内拉结钢板外侧混凝土保护层只有20 mm,且钢板拉结带没有采取抗滑移措施,导致混凝土和钢板的粘结不足;墙体的最终破坏仍集中在墙体根部,发生弯曲型破坏,钢板拉结带处的损伤没有影响墙体的主要破坏形式,对墙体的正截面性能影响甚小。拉结带处的混凝土脱落并不是试验所期望的损伤形态,在后期的研究中,应减少Z形钢板拉结带的翼缘宽度,增加与混凝土的粘结措施,避免出现此种现象。由于试验操作的问题,SW-B实际加载位移只有其他试件的65%。墙体破坏形态见图4。
3 试验结果及分析
3.1 承载力与位移
各阶段的试验结果如表3所示,荷载定义如表4所示。极限位移角θu =Δu/H,H为加载点距离墙底的截面高度;延性系数μ=Δu/Δy。
由表3可知,在轴压比不大于0.15时,相比于SW-B,SW-C的屈服荷载提高了59.8%,峰值荷载仅增大16.35%;较大轴压比下,SW-D的开裂荷载较SW-C增长了70.53%,峰值荷载仅提高了1.77%,表明峰值荷载对轴压比变化的敏感程度较小;SW-CFT墙的Δc和Δy 均比SW-A大,表明其延性比现浇试件好;SW-CFT墙的极限位移角和延性系数会随着轴压比的增大而减小,表明轴压比增大对SW-CFT墙的延性会有一定的削弱作用,但轴压比较大的SW-D试件,其θu和μ分别为1/55和3.68,与SW-A试件相比,仍然有所提高,表明SW-CFT墙的抗震性在高轴压下仍然比现浇剪力墙优异。
3.2 滞回曲线
试件滞回曲线如图5所示,曲线的形状由“梭”形逐渐转变为"弓"型,其包络面积随加载过程逐步变大。随着反复荷载的施加,墙板的刚度逐渐减小,主要是由于墙体出现裂缝、端柱塑性发展导致的。SW-A墙体的曲线“捏缩”现象比SW-CFT墙更明显;比较图5(a)、(c)可知,相同轴压比下,SW-C的承载力和抗震性能比SW-A更优异;对比图5(b)、(c)、(d)可知,SW-CFT墙滞回环面积相差不大,说明不同轴压比下SW-CFT墙的耗能能力相当。由于试验加载仪器的原因,SW-B实际加载位移仅是其他试件的65%。虽然SW-B的滞回环面积小于SW-C/D,但曲线走向与SW-C/D相似,且中部捏拢较轻。
3.3 骨架曲线
试件的骨架曲线如图6所示。从图6可知,各墙体的初始刚度基本一致,开裂之后,骨架曲线坡度出现不同程度下降,加载至峰值荷载以后,曲线开始下降;加载后期,SW-CFT墙表现出更高的承载力和刚度,SW-B/C/D的承载力较SW-A分别提高29.8%、50.9%、53.6%;SW-D试件在达到峰值荷载之后出现陡降现象,说明较大的轴压比下SW-CFT墙体的延性较差,但性能依旧优于SW-A。
3.4 刚度退化
墙体的刚度退化曲线如图7所示,曲线上的特征点为初始点、开裂点、屈服点、峰值点和极限点,从图7可知,SW-C/D的初始点刚度比SW-A略大,且各墙体的刚度退化规律基本一致;SW-CFT墙的刚度和抗侧性能始终优于SW-A;并且,随着轴压比的增加,SW-CFT墙的抗侧刚度呈递增趋势,说明增加轴压比可以提高剪力墙抗侧刚度;SW-A刚度衰减速度比SW-CFT墙更快,说明钢管的设置可以较好地减缓墙体整体刚度的衰减。
3.5 耗能能力
由表5可知,峰值荷载下,SW-C/D的累积耗能比SW-A分别提升了80.3%、62.1%,能量耗散系数E较SW-A分别提高了32.1%和24.6%,表明SW-CFT墙的耗能能力比SW-A更为突出。原因在于SW-CFT墙的变形能力较好,试验中,裂缝分布更加均匀,细小的裂缝不断扩展,扩展过程中,内部骨料不断摩擦,从而吸收了大量的能量,钢管屈服后进入塑性耗能阶段,也使得SW-CFT墙的耗能能力更好;而SW-C和SW-D的Q值和E值相差不大,说明轴压比对SW-CFT墙耗能能力影响不大。极限荷载下SW-C/D的Q值和E值均比SW-A高,与峰值荷载下的变化相同。
4 正截面受弯承载力分析
4.1 屈服承载力分析
试验用SW-CFT墙按高悬臂剪力墙分析,平截面假定适用于此类悬臂墙[4]。考虑屈服状态下各试件截面应力、应变的分布如图9所示。图10给出了屈服点的确定方法[19]。
由图10可得截面屈服曲率[20]为φy= faEa(hw0-xy)
(3)式中:xy为截面屈服时受压区高度;hw0=hw-aa,aa为受拉钢管截面型心到截面边缘的距离,取aa=hf/2。
4.4 算例验证
XTRACT软件可以完全交互地快速进行混凝土钢组合结构截面的承载力分析。以SW-CFT截面为计算对象,对轴压力和水平荷载受力工况下的正截面受压承载能力极限状态进行分析,直接形成截面轴力弯矩曲线,将结果与试验值进行对比。模型中,不考虑钢管和混凝土之间的滑移,预制与现浇混凝土按一体考虑。
模拟采用的本构模型如图11所示。以SW-C为例,截面长1 200 mm,宽200 mm。截面分3层,上下两层为预制混凝土,中间为现浇混凝土。截面布置8根直径12 mm的竖向钢筋;两端为方钢管,内部现浇混凝土。模型中所用混凝土、钢筋和钢材的特性参数取实测值。建模过程分为定义材料、截面定义、网格划分(自动划分三角形网格)、荷载施加、结果分析几个主要过程。以SW-D试件为例,界面定义及网格划分如图12所示,模拟结果如图13所示。
XTRACT计算的动态图显示,截面受压区高度先变小后变大,由图13(a)可知,蓝色区域为截面受压区,由于钢管的存在,边缘混凝土不会脱落,最终导致墙体外边缘钢管出现破坏,与试验的最终破坏模式一致;由图13(b)试件轴力弯矩关系曲线可知,B点为大小偏压分界点,此时极限弯矩对应的承载力见表7。
由表7可以看出,实测值与模拟值吻合较好,因此,SW-CFT墙的水平承载力可以使用XTRACT軟件进行计算。
5 结论
通过试验和计算分析,得到以下结论:
1)现浇混凝土剪力墙和SW-CFT墙均发生弯曲型破坏;不同轴压比下SW-CFT墙的破坏模式相同。
2)随着轴压比的增加,SW-CFT墙的屈服荷载和峰值荷载均出现不同程度的提高,且屈服荷载提高程度较大;在低轴压比下,SW-CFT墙的耗能能力明显较现浇混凝土墙高,轴压比对SW-CFT的耗能能力影响不大。
3)理论公式可以较好地计算SW-CFT墙的承载力,而SW-CFT墙的水平承载力可以使用软件XTRACT进行模拟。
参考文献:
[1] THOMSEN J H IV, WALLACE J W. Displacement-based design of slender reinforced concrete structural walls: experimental verification [J]. Journal of Structural Engineering, 2004, 130(4): 618-630.
[2] HARRIES K A, MCNEICE D S. Performance-based design of high-rise coupled wall systems [J]. The Structural Design of Tall and Special Buildings, 2006, 15(3): 289-306.
[3] HUMAR J, FAZILEH F, GHORBANIE-ASL M, et al. Displacement-based seismic design of regular reinforced concrete shear wall buildings [J]. Canadian Journal of Civil Engineering, 2011, 38(6): 616-626.
[4] 马恺泽, 刘伯权, 梁兴文. 型钢混凝土剪力墙的设计方法[J]. 中南大学学报(自然科学版), 2013, 44(9): 3807-3814.
MA K Z, LIU B Q, LIANG X W. Design method of steel reinforced concrete shear walls [J]. Journal of Central South University(Science and Technology), 2013, 44(9): 3807-3814.(in Chinese)
[5] 梁兴文, 马恺泽, 辛力, 等. 直接基于位移的钢骨混凝土剪力墙结构抗震设计方法研究[J]. 建筑结构学报, 2009, 30(Sup2): 159-164.
LIANG X W, MA K Z, XIN L, et al. Direct displacement-based seismic design method of steel reinforcement concrete wall building[J]. Journal of Building Structures, 2009, 30(Sup2): 159-164.(in Chinese)
[6] 连星, 叶献国, 蒋庆, 等. 叠合板式剪力墙恢复力模型特征参数计算方法[J]. 华侨大学学报(自然科学版), 2010, 31(1): 88-94.
LIAN X, YE X G, JIANG Q, et al. The calculating method about character parameter of the superimposed slab shear walls restoring force model [J]. Journal of Huaqiao University(Natural Science), 2010, 31(1): 88-94.(in Chinese)
[7] 连星, 叶献国, 张丽军, 等. 叠合板式剪力墙的有限元分析[J]. 合肥工业大学学报(自然科学版), 2009, 32(7): 1065-1068.
LIAN X, YE X G, ZHANG L J, et al. Finite element analysis of the superimposed slab shear walls [J]. Journal of Hefei University of Technology(Natural Science), 2009, 32(7): 1065-1068.(in Chinese)
[8] 钱稼茹, 魏勇, 赵作周, 等. 高轴压比钢骨混凝土剪力墙抗震性能试验研究[J]. 建筑结构学报, 2008, 29(2): 43-50.
QIAN J R, WEI Y, ZHAO Z Z, et al. Experimental study on seismic behavior of SRC shear walls with high axial force ratio [J]. Journal of Building Structures, 2008, 29(2): 43-50.(in Chinese)
[9] 钱稼茹, 江枣, 纪晓东, 等. 高轴压比钢管混凝土剪力墙抗震性能试验研究[J]. 建筑结构学报, 2010, 31(7): 40-48.
QIAN J R, JIANG Z, JI X D, et al. Experimental study on seismic behavior of steel tube-reinforced concrete composite shear walls with high axial compressive load ratio [J]. Journal of Building Structures, 2010, 31(7): 40-48.(in Chinese)
[10] 侯和濤, 程积润, 曲哲, 等. 钢管混凝土边缘约束叠合剪力墙抗震试验研究[J]. 湖南大学学报(自然科学版), 2017, 44(5): 27-36.
HOU H T, CHENG J R, QU Z, et al. Experimental study on the seismic behavior of concrete filled tube-confined sandwich shear walls [J]. Journal of Hunan University(Natural Sciences), 2017, 44(5): 27-36.(in Chinese)
[11] 王滋军, 刘伟庆, 翟文豪, 等. 新型预制叠合剪力墙抗震性能试验研究[J]. 中南大学学报(自然科学版), 2015, 46(4): 1409-1419.
WANG Z J, LIU W Q, ZHAI W H, et al. Experimental study on seismic behavior of new type reinforced concrete composite shear wall [J]. Journal of Central South University(Science and Technology), 2015, 46(4): 1409-1419.(in Chinese)
[12] 王滋军, 李向民, 王宇, 等. 带有约束边缘构件的预制叠合剪力墙抗震性能试验研究[J]. 中南大学学报(自然科学版), 2016, 47(8): 2759-2767.
WANG Z J, LI X M, WANG Y, et al. Experimental study on seismic behavior of reinforced concrete composite shear wall with confined boundary member [J]. Journal of Central South University(Science and Technology), 2016, 47(8): 2759-2767.(in Chinese)
[13] PLUMIER A, DRAGAN D, HUY N Q, et al. An analytical design method for steel-concrete hybrid walls [J]. Structures, 2017, 9: 185-199.
[14] EPACKACHI S, WHITTAKER A S, AREF A. Seismic analysis and design of steel-plate concrete composite shear wall piers [J]. Engineering Structures, 2017, 133: 105-123.
[15] EOM T S, NAM H S. Load contour method for biaxial design of reinforced concrete L-shaped structural walls [J]. Engineering Structures, 2017, 146: 148-157.
[16] 建筑抗震设计规范: GB 50011—2010 [S]. 北京:中国建筑工业出版社, 2016.
Code for seismic design of buildings: GB 50011-2010 [S]. Beijing: China Architecture & Building Press, 2016. (in Chinese).
[17] 混凝土结构设计规范: GB 50010—2010 [S]. 北京:中国建筑工业出版社, 2015.
Code for design of concrete structures: GB 50010-2010 [S]. Beijing: China Architecture & Building Press, 2015. (in Chinese).
[18] 日本建筑基準法[Z].平成十四年七月十二日法律第八十五号.
Japan building standards law [Z]. Law No.85, 2002.7.12.(in Japanese).
[19] 冯鹏, 强翰霖, 叶列平. 材料、构件、结构的“屈服点”定义与讨论[J]. 工程力学, 2017, 34(3): 36-46.
FENG P, QIANG H L, YE L P. Discussion and definition on yield points of materials, members and structures [J]. Engineering Mechanics, 2017, 34(3): 36-46.(in Chinese)
[20] PRIESTLEY M J N, KOWALSKY M J. Aspects of drift and ductility capacity of rectangular cantilever structural walls [J]. Bulletin of New Zealand National Society for Earthquake Engineering, 1988, 31(27): 73-85.
(编辑 王秀玲)
