基于SEOA算法的水库调度优化配置模型应用研究

陈 哲， 杨 侃， 吴 云， 汤梓杰， 张天衍， 赵友成

(1.河海大学 水文水资源学院， 江苏 南京 210098； 2.山西水利职业技术学院， 山西 运城 044004； 3.句容水利农机局， 江苏 句容 212400)

1 研究背景

在最小缺水量的水库调度中，旨在寻找水库的最佳调度过程来满足水库下游水资源配置时的缺水量最小。水库的优化调度在对下游的水量调配过程中，可以有效地取得最优的调度过程线。目前一般的优化算法分为两种类型，一种是以动态规划[1]为主的数学规划方法。随着所要求解问题的难度和复杂性的提高以及计算规模的逐渐扩大，动态规划等数学方法会出现“维数灾害”这样标志化的问题。针对这一问题，学者们进行了许多研究，比如负荷分配、逐步优化等一系列降维的方法[2]，随着科学技术的不断发展和计算机的普及也让这个问题得以缓解[3]。另一种则是以遗传算法等为代表的启发式优化算法[4]，这些方法一般都是以随机生成个体为开始，很好地处理了数学规划方法的维数灾害问题。在进一步的发展中，学者们对优化算法也进行了进一步的改进，如陈梁等[5]对遗传算法的初始种群进行调整，使用贪婪算法产生初始种群；又如陈丹丹等[6]使用图像拼接寻找最佳缝合线来减少计算量。但始终存在着局部收敛的问题。

社会情感优化(SEOA)算法由我国学者崔志华提出，其代表了一种新型的模拟人类社会群体行为的智能优化算法，算法收敛效率更高[7]。本文将采用社会情感算法来解决水库调度最小缺水量问题，并且根据算法的个体生成以及收敛速度的问题，尝试进行直线优化和动态阈值改进，通过计算实例对该算法的模型性能进行探讨，并提出有效度函数对算法进行评价。

2 研究方法

2.1 模型建立

2.1.1 目标函数 以调度期内的水库下游缺水量最少作为目标函数：

(1)

式中：T为调度段时期，月;Nt为第t时段的总需水量，m3;St为第t时段的总供水量,m3。

2.1.2 约束条件

(1)水量平衡约束

Vt+1=Vt+(Qt-Jt-Mt)·Tt

(2)

式中：Vt+1、Vt为第t时段末、初水库蓄水量，m3；Qt、Jt、Mt为第t时段的入库流量，弃水流量和损失流量，m3/s。

(2)水位约束

Zmin,t≤Zt≤Zmax,t

(3)

式中：Zmin,t、Zt、Zmax,t分别为第t时刻下限水位、计算水位、上限水位，m。

(3)流量约束

qmin,t≤qt

(4)

式中：qmin,t、qt分别为最小下泄流量、计算下泄流量，m3/s。

(4)调度期初、末控制水位约束:

(5)

2.2 社会情感优化算法

在人类社会中，由于各个人不同的遭遇和不同的情绪特征，每个人往往会采取不同的行为以获得不同的评价[8-9]。其数学表述如下：

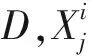
(6)

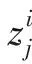
由于初始种群在整个搜索空间内随机分布，则初始种群个体生成如下式：

(7)

式中：zdmax、zdmin分别为该d维搜索空间的最大值与最小值，即上限水位与下限水位； Rand[0,1]表示在[0,1]区间的一个随机数。

(8)

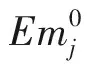
步骤2：社会评价值。根据每一个个体所处位置进行社会评价值计算，计算所得的最优值记录为社会种群历史最优社会评价值，同理最劣值为社会种群历史最差社会评价值。个体的最优社会评价值记录为该个体的历史最优社会评价值，并记录上述社会评价值的相应位置[8-10]。模型建立时采用罚函数法将目标函数公式(1)进行改造，作为本数学模型的社会评价值：

(9)

(10)

式中：Δ为情绪指数迭代参数。

步骤4：个体位置更新。初始种群的所有个体情绪指数都为1，个体认为此次迭代结果正确，则学习方向即为吸取社会评价值最差的L个个体的经验教训，即更新方向为远离社会评价值最差的L个个体的位置：

(11)

当迭代到第i代(i=1，2，…，imax)，个体间的情绪指数产生了明显的差异，根据个体情绪指数与情绪阈值Th1、Th2的关系，将个体分为3种不同的类型进行不同的更新策略：

(12)

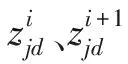
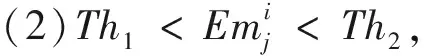
(13)

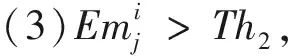
(14)

步骤5：判断终止。若满足终止条件，则迭代终止，输出种群最优解；反之，令i=i+1，进行下一步迭代，重复步骤2～5，直到满足终止条件。

2.3 社会情感优化算法的改进

如前文所述，新型智能优化算法大多都存在一定的缺陷，例如计算中收敛速度不稳定、易出现局部最优解等问题，作为新型智能优化算法的社会情感算法也是如此，由此针对此问题提出两种对于SEOA算法的优化[11-12]。

2.3.1 初始种群的直线优化 基本的智能算法对于初始种群的生成大多偏向于随机，这对于算法的收敛速度影响较大，故针对生成初始个体方法的不足，提出直线优化过程。

“初始种群直线优化”即生成的初始个体采用相同的位置在各个维度上均采用上、下限的平均值生成初始个体：

(15)

式中：zdmax，zdmin表示该d维搜索空间的最大值与最小值，即上限水位和下限水位。

基于公式(15)生成的初始个体在进行迭代计算过程中向两边扩散计算，更利于最优解的收敛，从而有利于全局收敛。

2.3.2 情绪阈值的动态设计 基本的社会情态优化算法的情绪阈值在计算过程中并不会发生变化，这样设计的优点是计算过程简单，但在实际的操作过程中收敛速度偏慢，故提出对情绪阈值进行动态设计，以解决收敛速度不足的问题。

情绪阈值的动态设计操作为在进行第i次迭代计算的过程中将个体的情绪指数进行排序，取排序为[j/3]处的个体情绪值为Th1，取排序为[2j/3]的个体情绪值为Th2，这样在计算的过程中可以使种群个体更有效地进行策略选择。

(16)

图1为改进前后社会情态优化算法的流程对比。

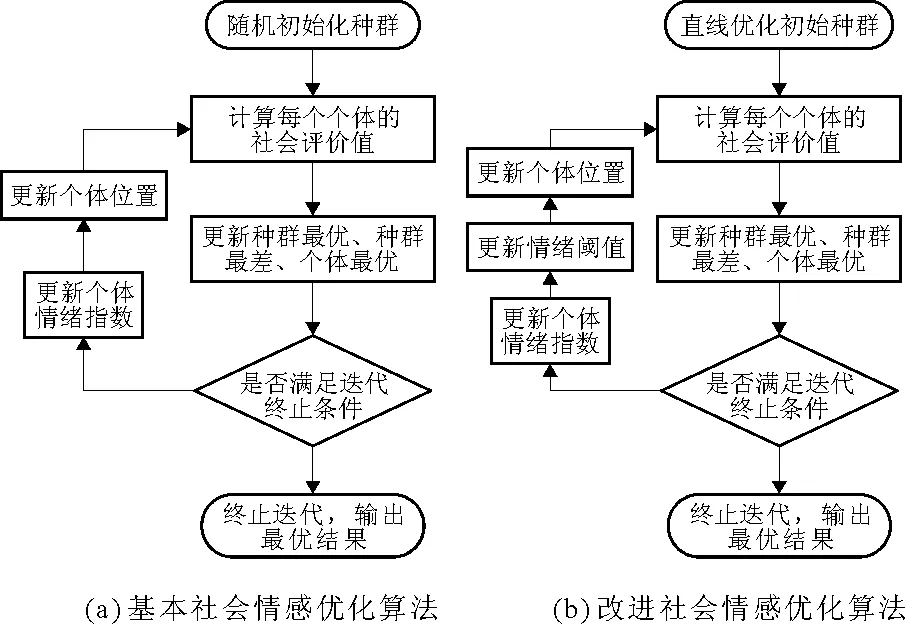
图1 改进前后社会情态优化算法的对比流程图

2.3.3 求解步骤 采用改进的社会情感优化算法解决水库调度最小缺水量问题的具体步骤如下：

步骤1：初始化。初始参数的确定包括种群规模H、情绪指数初始阈值Th1、Th2、情绪迭代参数Δ、最大迭代次数kmax、学习因子b1、b2、b3和差个体数L等等。

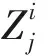
规定各个搜索维度的上、下限为水库调度中的上限水位和下限水位，生成的初始个体及之后的计算个体必须在上下限之间，按照公式(15)生成初始个体，水库调度期初水位和末水位按照约束条件公式(5)进行取值，初始的情绪指数按照公式(8)进行取1。

步骤2：社会评价值计算。由于水库调度中的约束条件往往是非线性的，所以采用罚函数法，根据公式(9)进行各个社会评价值的计算。记录每一次计算的目标函数值以及所要利用的各个社会评价值，并记录上述的调度过程曲线[13]。

步骤3：情绪指数更新。首先判断当前值是否为个体最优社会评价值，再根据公式(10)更新个体情绪值。

步骤4：情绪阈值更新。在计算完所有的个体情绪值后，对所计算的情绪值进行排序，并按照公式(16)选取个体进行情绪阈值更新。

步骤5：个体位置更新。根据公式(11)～(14)，利用上述记录的3个社会评价值对个体进行位置更新，更新后的个体若超过上限水位则取上限水位，若低于下限水位则取下限水位。

步骤6：判断终止。判断迭代次数是否达到最大迭代次数kmax，若小于kmax，则令k=k+1重复步骤2～ 6直到kmax，停止迭代，输出最优水位调节过程以及最小缺水量结果。

3 实例分析

3.1 研究区域概况

本文以山西大水网的第一横地区的上游的东榆林水库作为计算区域。东榆林是一座以灌溉为主，

兼顾防洪的中型水库，总库容6 500×104m3，最大泄流量2 811 m3/s，校核洪水位1 042.1 m，死水位1 035 m[14]。水库位于桑干河干流上游，上接引黄工程流域。由于山西地区总体缺水，在引黄补给的同时，东榆林水库通过对上游来水进行调节来达到对下游山阴县、怀仁县以及应县的持续供水。由于地区缺水，将对2020年的水库调度方案进行规划计算。研究区范围示意图见图2，供水系统结构概化图见图3。

图2 研究区范围示意图

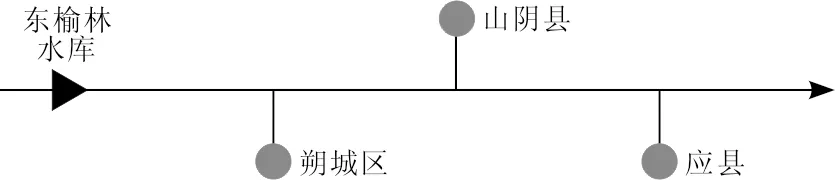
图3 供水系统结构概化图

3.2 需水量预测结果

通过回归分析法预测得到2020年的需水量，见表1。

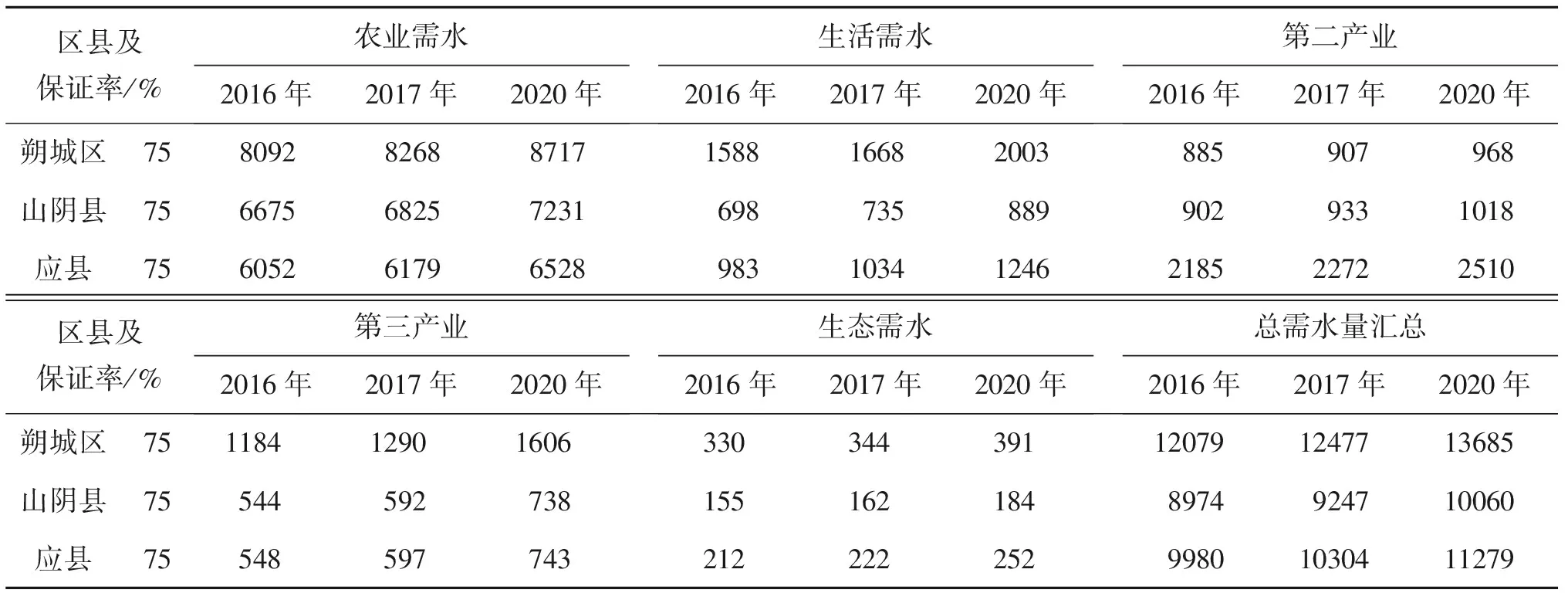
表1 东榆林水库下游3区县2020年需水量预测 104 m3

3.3 优化配置结果

通过模型建立计算所得3个区县2020年的用水量月分配情况如表2所示。

表23区县2020年用水量月配置预测结果104m3

月份朔城区山阴县应县1217.4159.8179.12108.779.989.63679.3499.3559.842037.81497.91679.451630.21198.31343.561358.5998.61119.672717.01997.22239.282037.81497.91679.49326.0239.7268.710434.7319.6358.3111358.5998.61119.612679.3499.3559.8

由于采用折线图表示库水位调度曲线与实际较为接近，故对改进SEOA算法的调度结果进行展示，如图4所示。

3.4 算法性能分析

采用遗传算法、基本SEOA算法和改进SEOA算法分别对模型进行求解，使用动态规划算法求得问题在同等精度下的精确解，通过指标数η来判别算法性能：

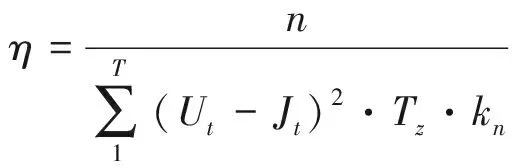
(17)

式中：Tz为实行所有计算所需要的时间,min；T为总计算时刻数；Ut、Jt分别为t时刻计算所得的最小缺水量以及同等精度下的最小缺水量的精确解，m3;n为迭代次数;kn为该迭代次数下的修正参数(n=1～10取1.1，n=10～100取1.3，n>100取1.5)。该函数使用前提为初始个体精度以及分段时长相同的情况才可以用来比较。

经过多次试算后选取的参数如表3所示。

表3中kmax可以进行变化以探求有效度是否能够有效地判别算法性能。

对每种算法采取了20次独立的计算，以保证计算结果具有一定的代表性，以统计所得出的最优值、平均值、标准差及耗时作为评价指标。

在处理器为Intel i5-8500、4G内存、window7操作系统的条件下进行数据计算，所得到的3种算法各个评价指标值如表4所示。

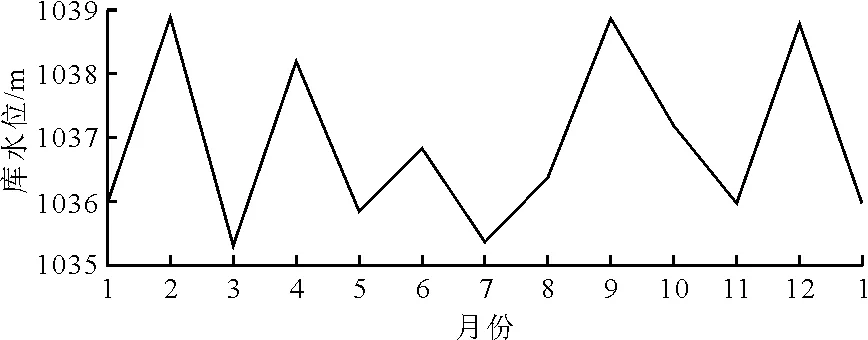
图4 2020年预测库水位调度曲线(改进SEOA算法)

表3 3种算法的参数选取

表4 3种算法的各评价指标数据比较

相比于传统的以动态规划为代表的数学规划方法，SEOA算法与遗传算法等智能算法能够很好地避免维数灾害这一问题。对于计算结果，在迭代次数为100的情况下，SEOA算法也能够给出和精确解十分接近的结果，而改进的SEOA算法能够很好地收敛于动态规划计算所得的精确解，具有一定的代表性。

对于3种算法的有效度函数η进行计算比较，改进SEOA算法η值最高，在同等精度计算的过程中相较于另外两个算法有着一定的优势，同时η对于算法的性能表达具有一定的代表性。

选取3种算法最优的一次迭代过程展示各个算法与迭代次数之间的关系作图5，以比较3种算法的收敛快慢。

图5 3种算法最小缺水量计算进化过程曲线比较

由图5可见，普通的SEOA算法对于计算个体的收敛速度比不上智能的遗传算法，但经过初始个体和情绪阈值的改进，收敛速度大为增加，并且计算出的结果也更加接近精确解。

4 结 论

本文通过采用SEOA算法对于东榆林水库地区进行最小缺水量问题的计算，并针对算法的初始种群的生成和情绪阈值的确定进行改进，取得了以下的成果和结论：

(1)SEOA算法作为新型的智能优化算法，能够很好地解决传统数学规划方法在求解问题较为复杂情况下的维数灾害问题，其初期收敛速度与其他传统启发式算法大致相同，同时能够得到较好的全局最优解。

(2)改进的SEOA算法在初始种群的生成上有着一定的优势，并且通过对于情绪阈值的更新，在同等迭代次数的情况下，达到全局最优解的可能性更高。与普通的SEOA算法相比，收敛速度有效增加，取得的计算结果更加准确，有着一定的实用价值。

(3)通过回归分析法以及水库蓄水容量曲线计算，成功预测了2020年朔州市3区县的需水量，得到了缺水量最小的水库水位调度曲线以及3区县的水资源优化配置，在解决实际问题中有着一定的实用价值。