空间充气薄膜衍射成像结构的热力耦合分析

孙向伟1，徐彦2*，王培栋2，方琴2朱东方34

1. 浙江大学 先进技术研究院，杭州 310027 2. 浙江大学 航空航天学院，杭州 310027 3. 上海航天控制技术研究所，上海 200233 4. 上海市空间智能控制技术重点实验室，上海 200233

近年来，随着高精度加工水平的不断提升，衍射成像系统成为空间光学领域的研究热点。空间光学遥感技术飞速发展，可以广泛应用于气象预报、军事监视以及地面成像观测等领域。衍射主镜可以采用薄膜材料作为基底材料，具有大口径、高分辨率、质量轻、可折叠展开、公差宽松等优点，可以由航天器搭载进入轨道，减少制造成本和发射成本[1-3]。空间充气薄膜衍射成像结构是一种充气展开式光学载荷，采用薄膜衍射成像系统，支撑结构采用充气展开结构[4]，最大程度地降低了载荷质量和发射体积，并有望实现巨型口径、轻质化、更高空间分辨率的空间光学载荷。

图1 MOIRE衍射望远镜概念图Fig.1 MOIRE diffraction telescope concept

美国国防预先研究计划局(DARPA)于2010年启动了MOIRE(Membrane Optic Imager Real-Time Exploitation)项目[4]，即空间薄膜衍射成像系统。MOIRE衍射望远镜概念如图1所示。该系统的主镜由两圈圆菲涅尔子镜组成，内圈圆镜的直径为1 m，外圈圆镜直径为1.5 m，内外圈圆镜共计36块。MOIRE项目的承包商美国鲍尔航空航天技术公司(BATC)、美国纳克训材料公司(Ne Xolve)和美国劳伦斯-利弗莫尔国家实验室(LLNL)在材料[5-6]、结构和光学性能测试[7]等方面完成了大量研究。

对于大型空间结构，空间热载荷是最重要的载荷之一，有必要研究结构在轨运行期间的瞬态热应力、热变形和热致振动[8-9]。航天器结构在空间环境影响下产生静动力响应，结构变形又会改变温度场分布。由于大型空间结构的大变形和非线性因素，温度场和结构响应之间存在明显的多场耦合效应。现有的航天器热设计大多关注热载荷对结构振动响应的单向影响，热力耦合研究则主要针对刚性结构，而柔性结构如充气薄膜结构热分析很少考虑热力耦合效应。随着柔性结构在大型航天器中广泛应用，有必要研究其热力耦合性能，从而为后续的热设计提供技术支撑。

本文针对充气薄膜衍射成像结构在轨运行时的热致变形问题，开展柔性结构热力耦合效应研究，通过建立顺序耦合求解框架，并对通用有限元软件进行二次开发，数值仿真了充气薄膜成像结构的热应力和热变形。

1 充气薄膜成像结构设计

空间充气薄膜衍射成像展开结构包括：薄膜衍射主镜、充气环管、充气直管、张拉索,整体模型如图2所示。薄膜衍射主镜、充气环管和充气直管均由透明聚酰亚胺薄膜制备而成。充气直管和充气环管粘接组成充气支撑结构，薄膜衍射主镜水平设置，中心圆形镜面直径为500 mm，圆形镜面周边均匀粘接有12跨的花边薄膜。花边薄膜形态为圆弧，跨度为0.142 m，跨高为0.015 m。薄膜衍射主镜通过12根张拉索和充气支撑结构连接，张拉索长度为0.25 mm。

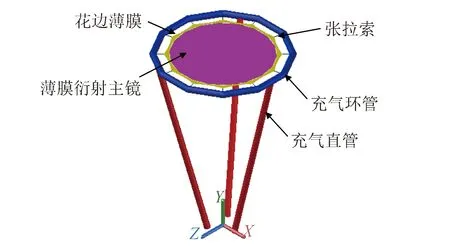
图2 充气薄膜衍射成像结构模型示意Fig.2 Model of membrane diffraction imaging structures

充气支撑结构包括充气环管和充气直管，充气环管采用12根充气短管首尾相接，充气环管内侧的内切圆半径为0.3 m，外侧的内切圆半径为0.332 m，截面直径为0.032 m。支撑结构中有3根充气直管和充气环管连接，两者内腔相通。充气直管的轴线长度为1 m，截面直径为0.03 m。其中充气直管和环管之间的相贯线为复杂的空间曲线，如图3所示。

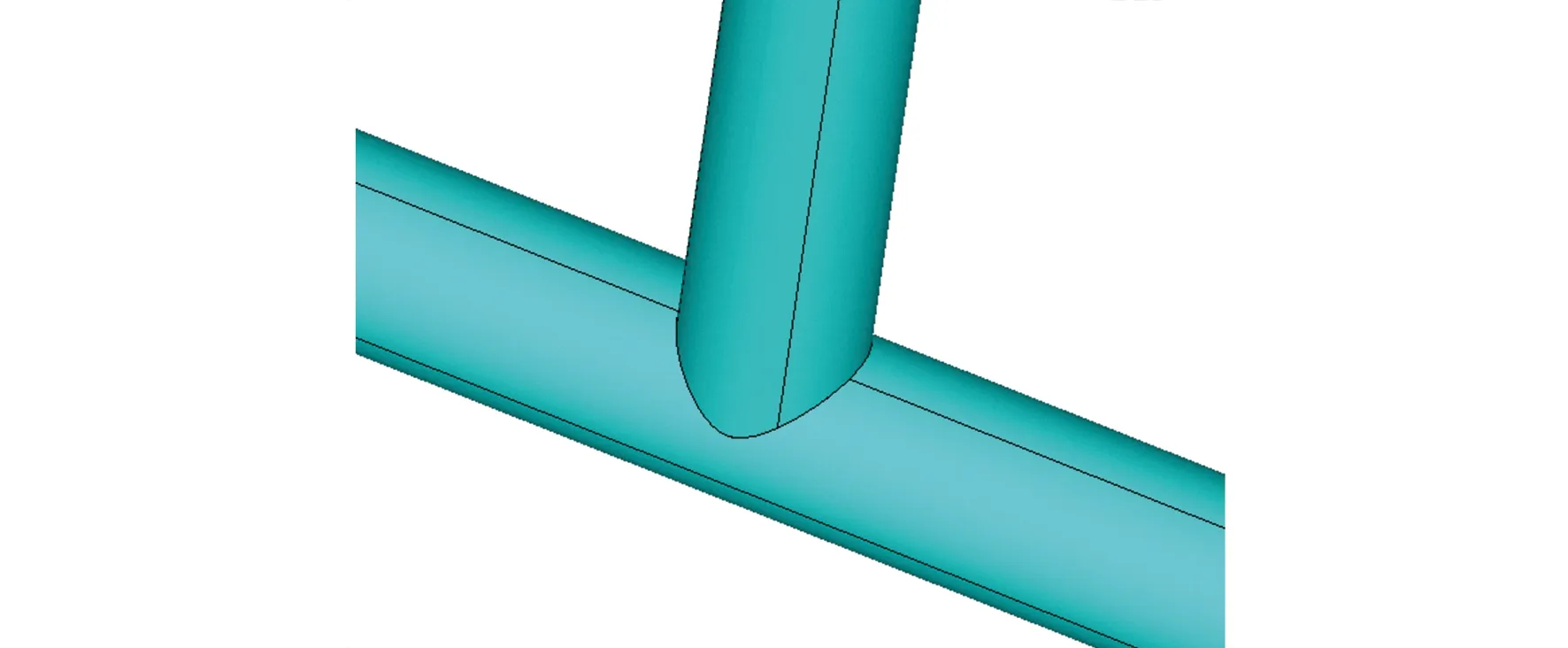
图3 充气直管和环管相贯线Fig.3 Intersecting lines of inflatable tube and ring pipe

研制了充气薄膜成像结构样机，并设计、研制了收纳结构和悬挂系统。充气薄膜成像结构样机的折叠收纳状态和完全展开状态如图4所示。

图4 充气薄膜成像结构样机Fig.4 Prototype of membrane diffraction imaging structures

2 瞬态传热和热弹性动力学分析

如前所述，为了研究充气薄膜成像展开结构的热力耦合效应，需要建立顺序耦合求解框架，包括主控模块、瞬态传热分析模块和热弹性动力学分析模块。下面简要介绍航天器结构的瞬态传热和热弹性动力学分析理论。

2.1 瞬态传热分析[10-11]

充气薄膜成像展开结构在轨周期运行时，相对于太阳和地球的位置和方向不断变化，外热流和辐射交换也在不断变化，所以某一时刻温度场的求解要进行瞬态传热分析。

温度场描述某一时刻物体中各点的温度分布，是时间和空间的函数。

T=f(x,y,z,t)

(1)

式中：x,y,z为空间坐标；T为温度；t为时间。式(1)表示三维的瞬态温度场。

一般用偏微分方程和其边界条件来描述温度场，根据温度场对应的泛函，由其等价的泛函极值方程来求得问题的解。由充气薄膜成像展开结构在空间环境中的热平衡关系，可得出薄壳单元的热平衡方程[10]。

σT4εdA+λ2TdV+∑aσT4εφijdA

(2)

式中：φ1、φ2、φ3、φij分别为太阳直接辐射、地球反照、地球红外辐射和部件之间辐射的角系数，它们均会随结构位移的不同而发生变化，本文只考虑太阳直接辐射和部件之间辐射，而没有考虑地球反照、地球红外辐射；c、a、λ、η、ε分别为材料热学性能中的比热、吸收率、热传导系数、反照率和材料黑度；ρ为材料密度；S为太阳常数；σ为斯特潘-波尔茨曼常数。

式(2)右端第1项为外热流，第2项为单元向空间辐射的热流，第3项为传导换热，第4项为单元间辐射换热，左端为单元内能的变化率。将上述方程左端项对时间域做有限差分展开，右端项用有限元方法求解，可得到下面的热平衡方程。

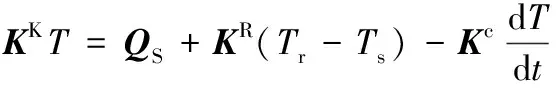
(3)

式中：KK为总热传导矩阵；KR为总热辐射矩阵；Kc为总热容矩阵；QS为外热流输入形成的节点热流失矢量；Ts为前一时刻物体表面的温度；Tr为辐射源的环境温度。应用差分法可求解上述热平衡方程，从而求得单元的时刻温度[8]。

2.2 热弹性动力学分析

充气薄膜成像展开结构三维热弹性动力学的基本方程及其边界条件[10]，即平衡方程如下：

σij,j+fi=ρui,tt+μui,t

(4)

式中：i,j,k,l为张量下标，取值为1,2,6；σij为应力张量；fi为体积力；ρui,tt和μui,t分别为惯性力和阻尼力；ρ为质量密度；μ为阻尼系数；ui，t和ui,tt分别为位移ui对时间t的一次导数和二次导数，即分别表示速度和加速度。

几何方程：

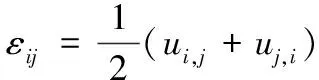
(5)

式中：εij为应变张量。

物理方程：

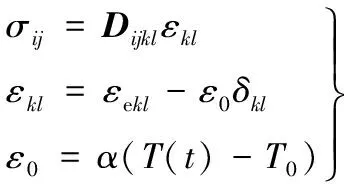
(6)

式中：Dijkl为弹性矩阵；ε为应变；α为材料的热涨系数；T(t)为t时刻的瞬时温度；T0为参考温度；下标e表示弹性。

边界条件：

(7)

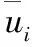
初始条件：

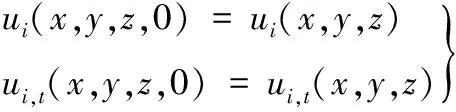
(8)

式中：ui(x,y,z)为初始位移；ui,t(x,y,z)为初始速度。

平衡方程式(4)及力的边界条件的等效积分形式Galerkin方法可表示如下：

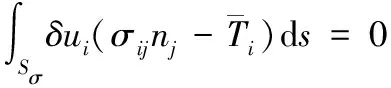
(9)

对式(9)的第一项v进行分部积分，并代入物理方程，则：

(10)

在动力分析中，引入时间坐标，分析中一般采用部分离散的方法，即只对空间域进行离散，并注意到结点位移变分δui的任意性，最终得到动力学系统的振动微分方程：

(11)

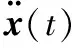
3 热力耦合分析框架及建模

3.1 顺序耦合分析框架

热力耦合问题分为两大类：一是热-结构材料性质变化的耦合问题；二是热-结构变形耦合问题。两种问题均先由热流的变化而引起结构温度场的变化。结构温度场的改变将引起结构材料性质的变化，进而引起结构位移和运动状态的变化，同时，温度场的变化以温度载荷的形式作用于结构，也将引起结构位移和运动状态的变化。由于涉及不同物理场之间复杂的相互作用和相互影响，很难用具体的数学表达式来描述物理场之间的耦合关系，所以分析任务具有很高的难度和复杂度。热力耦合场分析方法分为两类：直接耦合法[12]和顺序耦合法[13]。直接耦合法只有一个分析求解器，使用包含多场自由度的耦合单元，通过计算包含位移自由度和温度自由度的单元矩阵进行耦合。顺序耦合法先利用热有限元模型求解出结构的温度场，然后将温度场数据以温度载荷的形式加载到有限元模型的节点上，完成结构的热应力和热变形计算。

对于本文研究的空间薄膜衍射成像充气展开结构，由于在空间热环境中，聚酰亚胺薄膜材料在热弹性范围内，故只考虑热-结构变形耦合问题。直接耦合法使得热力耦合问题求解变得非常困难，为了最大限度地利用现有的求解器，本文采用顺序耦合分析框架。

基于有限元软件I-DEAS和ANSYS二次开发技术，通过自编写的MATLAB程序实现空间薄膜衍射成像充气展开结构的热力耦合分析。首先在ANSYS中进行几何建模、网格划分，得到有限元模型，然后提取节点、单元信息编写成I-DEAS有限元模型文件，设置轨道参数和求解控制参数等，并利用I-DEAS的TMG模块求得充气薄膜衍射成像结构的在轨瞬态温度场，导出其温度场结果文件；将温度场信息编写成ANSYS载荷加载的命令流文件，并设置约束条件进行瞬态动力学分析，求解得到充气薄膜衍射成像结构的热应力和热变形；变形后的结构模型传递给I-DEAS，用以下一个时间步的瞬态传热分析。充气薄膜衍射成像结构热力耦合分析的基本流程如图5所示。

在该流程图中，ANSYS中几何建模和瞬态动力学求解都采用二次开发语言APDL完成， I-DEAS的瞬态传热分析也是采用二次开发语言prg完成，采用自编写的MATLAB程序组织顺序耦合求解过程，后台调用ANSYS和I-DEAS进行求解，并进行两者之间的数据传递。

图5 热力耦合分析流程Fig.5 Process of thermal-structural coupling analysis

3.2 有限元建模

按照前述的热力耦合顺序分析框架，在I-DEAS软件的TMG模块进行瞬态传热分析，在ANSYS软件中进行热致变形和瞬态动力学分析，两部分分析需要采用同一有限元模型。空间薄膜衍射成像展开结构的ANSYS有限元模型如图6所示。结构各部件的材料属性设置见表1。充气支撑结构、薄膜主成像和花边薄膜采用SHELL181单元离散，张拉索采用link180单元离散，并设置为只拉。薄膜主成像和花边薄膜、张拉索中的预拉力通过降温法施加，通过在薄膜主成像和花边薄膜、张拉索的所有单元上施加-2℃的热载荷，从而获得薄膜衍射主镜和张拉索中的预应力场。

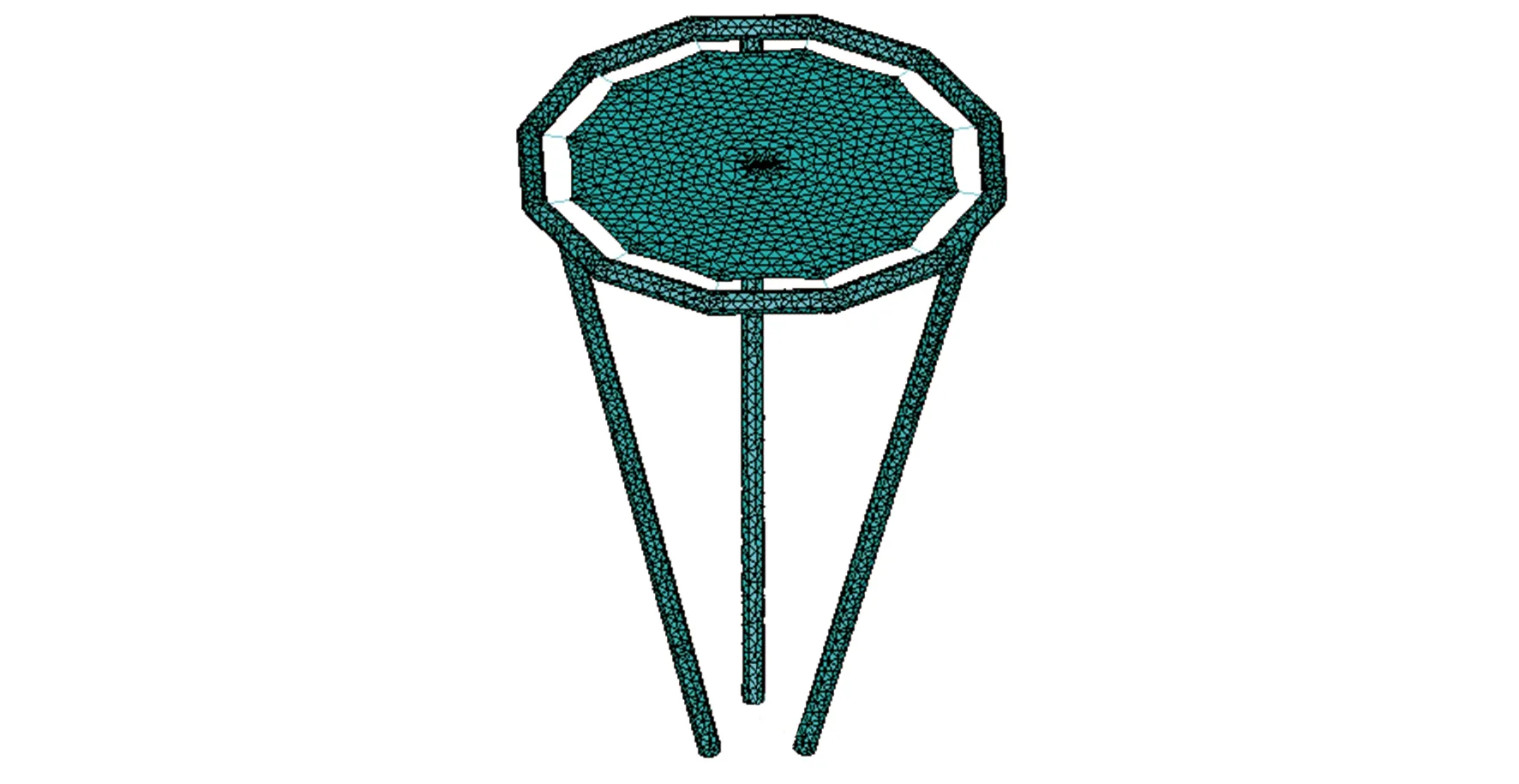
图6 有限元模型Fig.6 FEA model

采用相应的APDL语句自动提取单元与节点信息，并将其写入文本文件，在MATLAB程序中读取包含节点和单元信息的文件后，生成I-DEAS软件的prg文件，随后调用I-DEAS软件并读取prg文件，建立I-DEAS瞬态传热有限元模型。在瞬态传热有限元模型中，各部件材料的热物属性设置见表1。

表1 充气薄膜衍射成像结构各部件材料属性

在轨运行时，充气薄膜衍射成像结构的衍射主成像法向方向始终指向地球，即Z轴方向指向地球，X轴为充气薄膜衍射成像的飞行方向，瞬态传热有限元模型和在轨飞行如图7所示。由图7所示的结构姿态、飞行方向和轨道参数等可以确定结构所受的外热流，为瞬态传热分析提供热边界条件。

图7 充气薄膜衍射成像结构在轨飞行Fig.7 Flight of membrane diffraction imaging structures in orbit

轨道参数:轨道高度为1 098.9 km，周期为6 432.44 s，离心率为0，轨道倾角为0°。初始计算时刻选定在升交点，太阳位置为春分点，充气薄膜衍射成像展开结构的初始温度设定为290 K，初始时刻温度场分布见图8。充气薄膜衍射成像结构在轨飞行一个周期分为12个时间步，在一个时间步内，再设置12个计算点，本时间步的最后时刻温度场作为下一时间步的初始温度。

图8 0 s时刻的温度场Fig.8 Temperature field at 0 s

4 仿真结果分析

4.1 预应力模态分析

对空间薄膜衍射成像充气展开结构使用ANSYS进行预应力模态分析，当充气直管和环管内气压为1 000 Pa时，首先进行充气气压作用下的静力分析，然后进行模态分析，采用Block Lanczos方法(兰索斯法)分析结构的固有频率和振型。其中前10阶频率见表2，前4阶频率对应的振型见图9。

由模态分析结果可知，当充气直管和环管内气压为1 000 Pa时空间薄膜衍射成像充气展开结构的基频为2.185 Hz，设计气压满足要求，结构刚度较好。

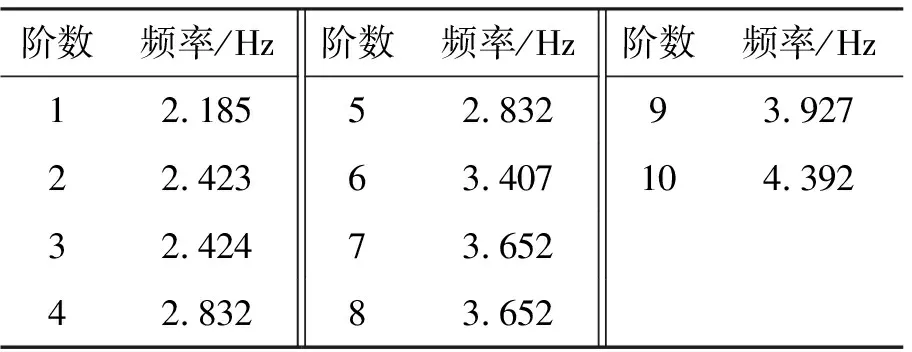
表2 前10阶频率

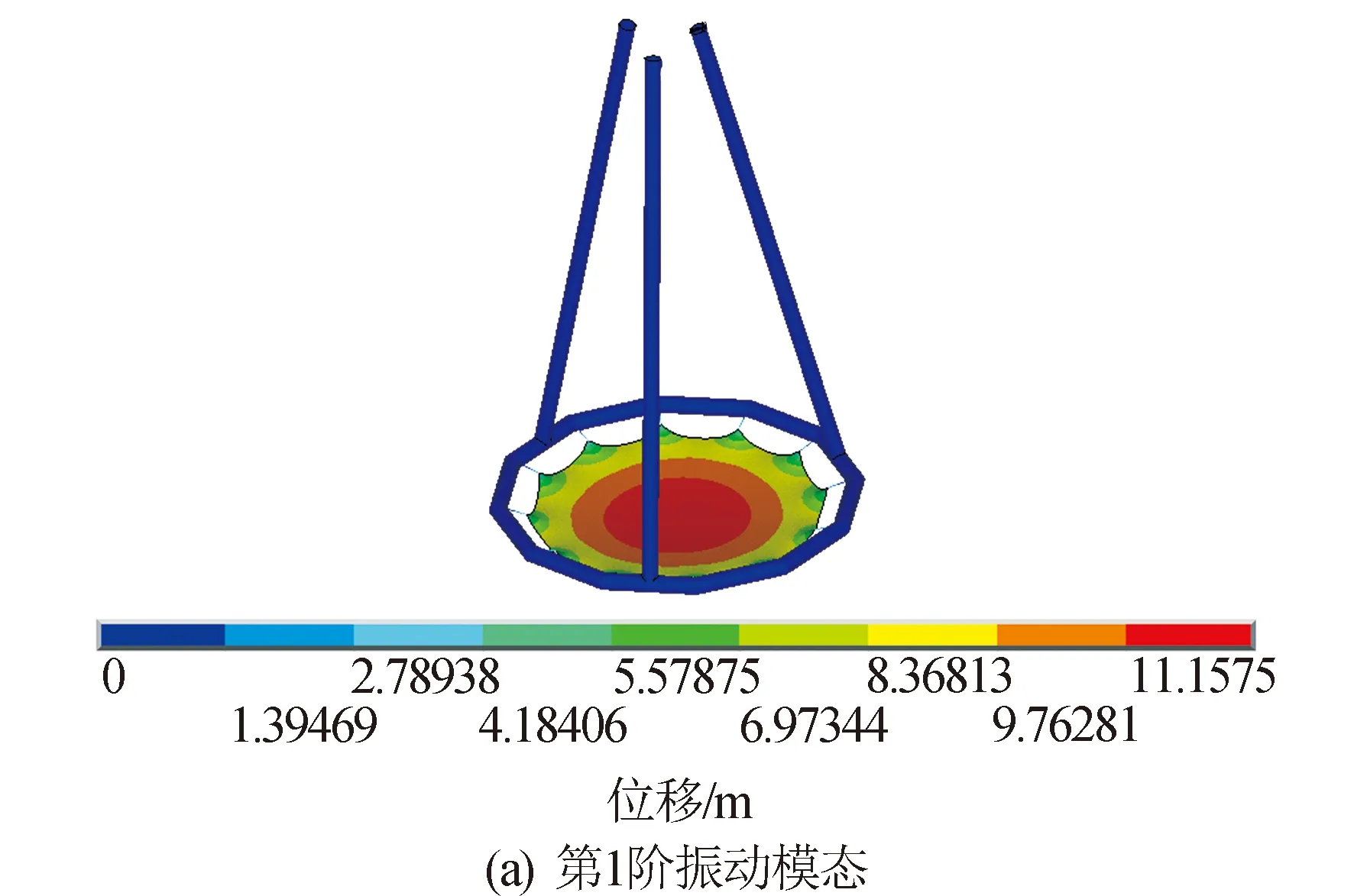
图9 前4阶振动模态Fig.9 First four vibrational modes

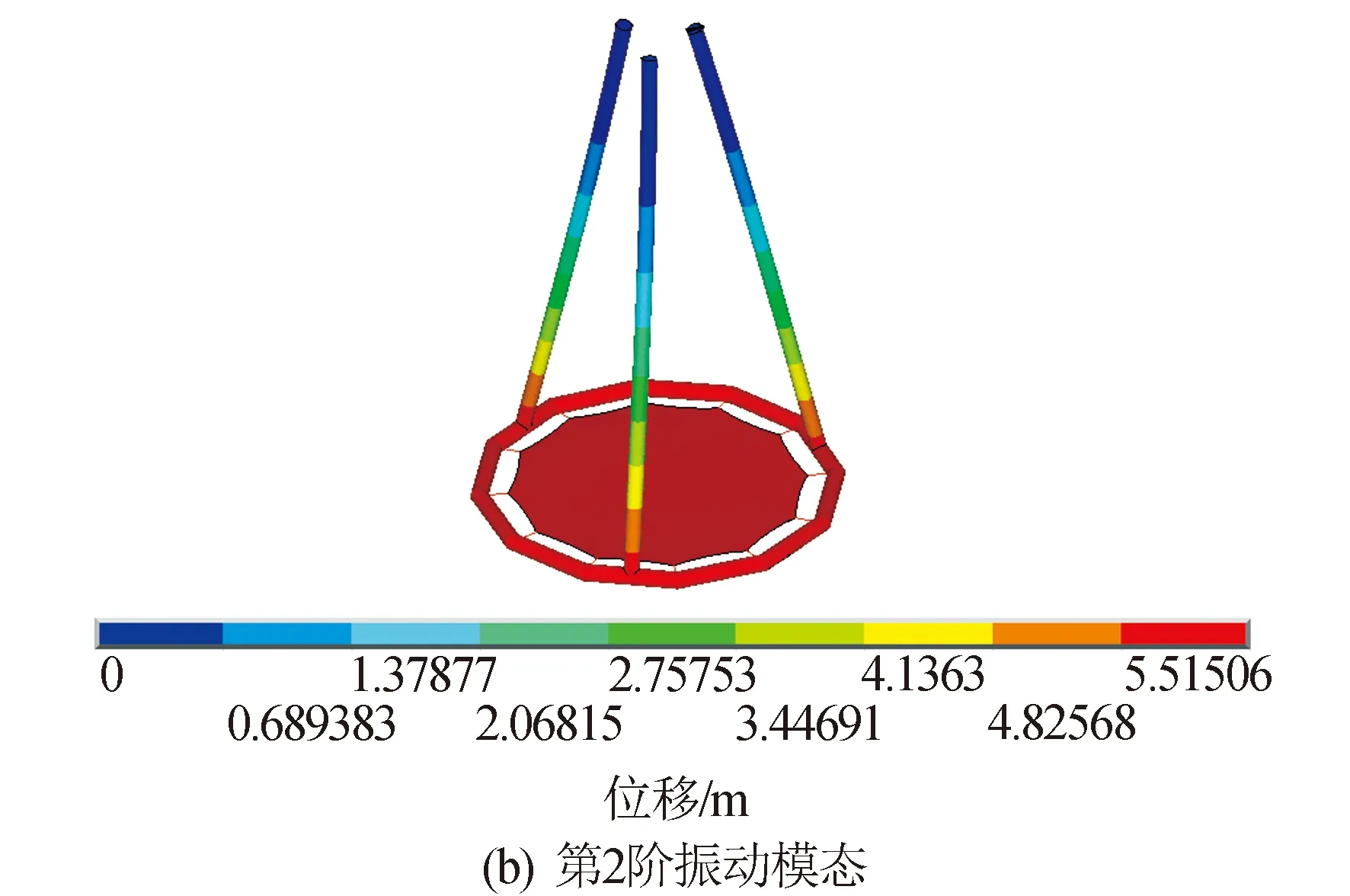
续图9Fig.9 Continued

4.2 热力耦合分析

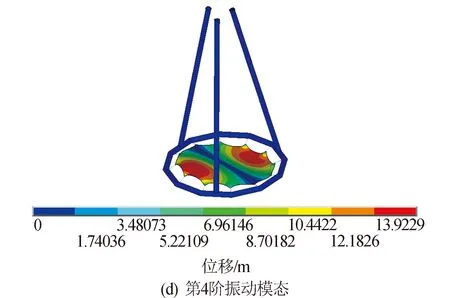
通过充气薄膜衍射成像结构的热力耦合分析，可以得到结构在各个时刻的温度场分布、热变形、热应力响应。限于篇幅，其中4个时间步(分别是1 608.10 s、3 216.22 s、4 824.34 s、6 432.44 s)的瞬态温度场分布、热变形分布、热应力分布、衍射主成像成像面中心节点Z方向位移响应曲线如图10～图13所示。

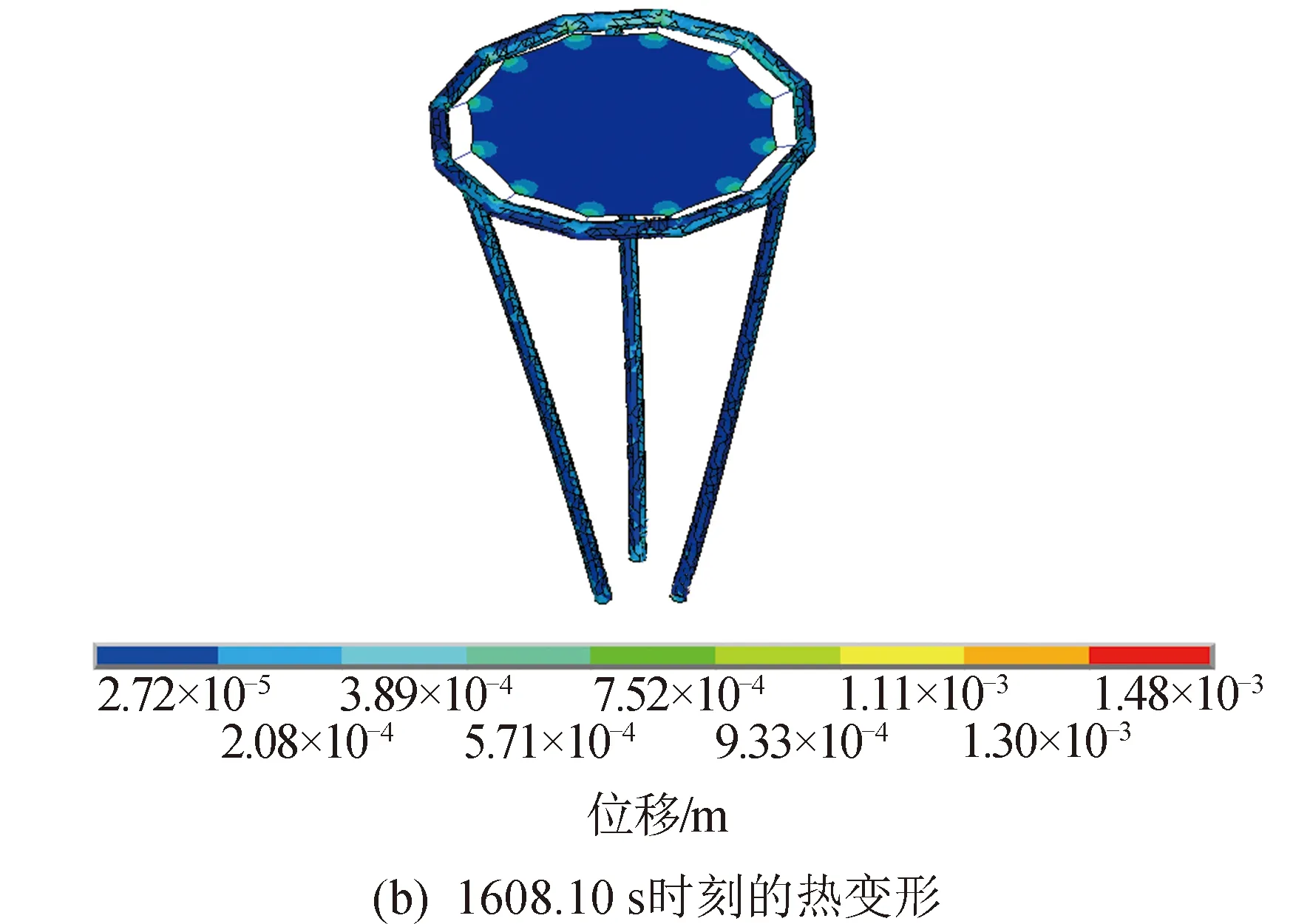
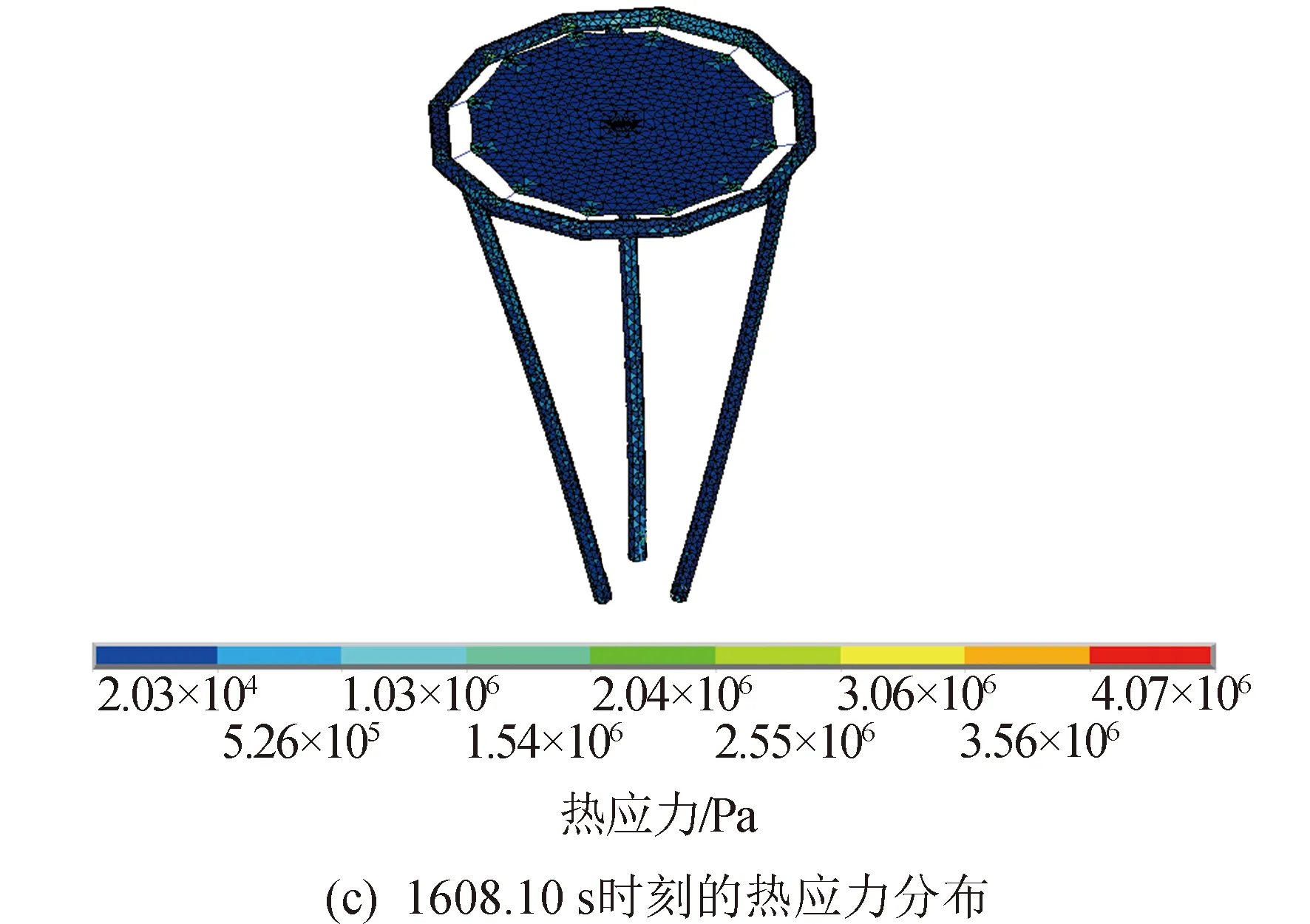
图10 第3个时间步热力耦合分析结果Fig.10 Third step thermodynamic coupling analysis results

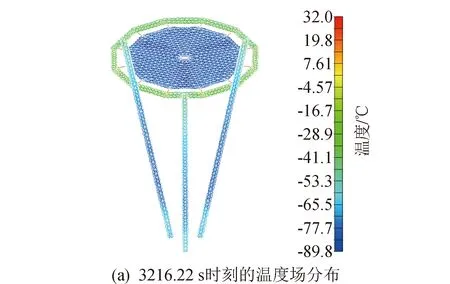
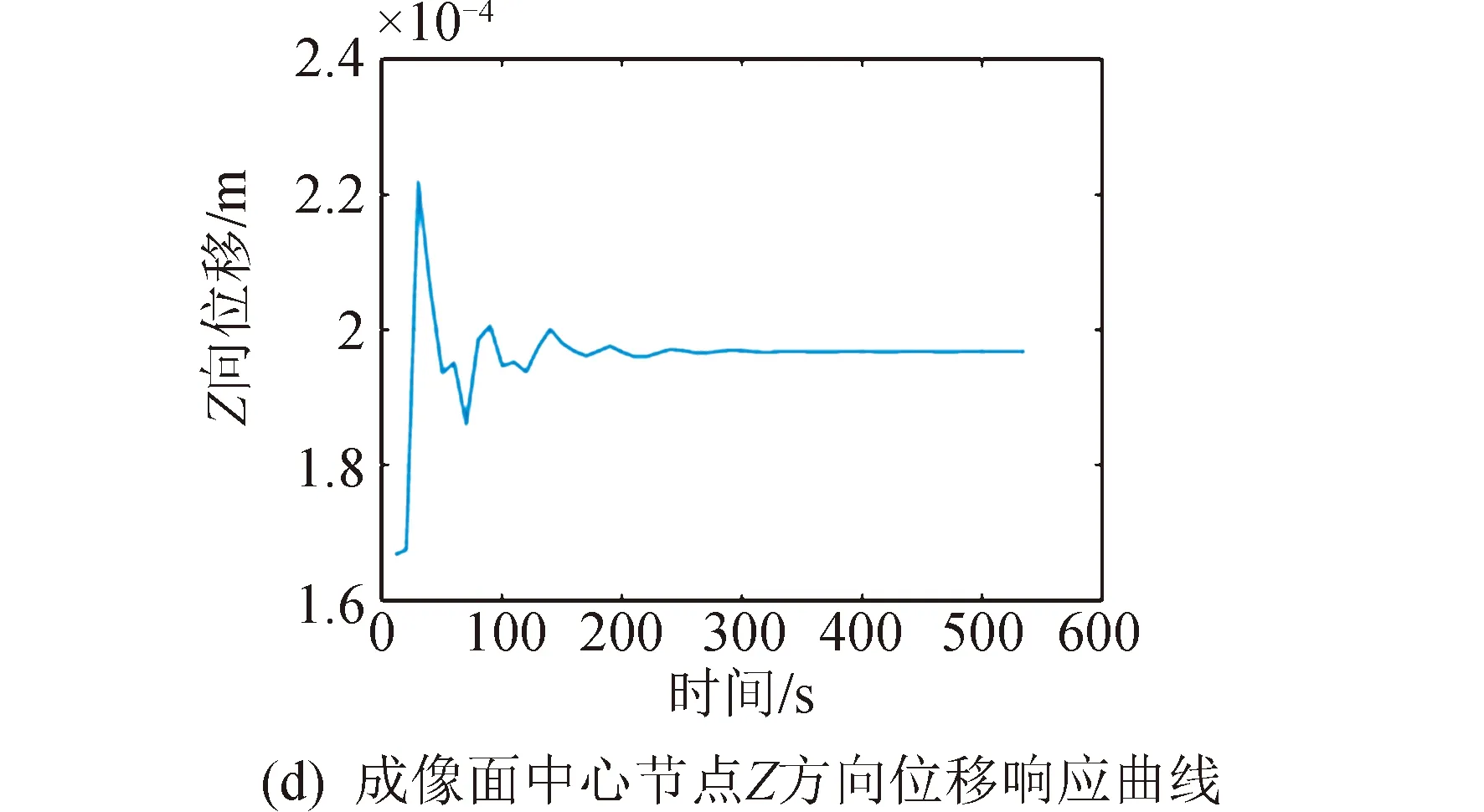
图11 第6个时间步热力耦合分析结果Fig.11 Sixth step thermodynamic coupling analysis results

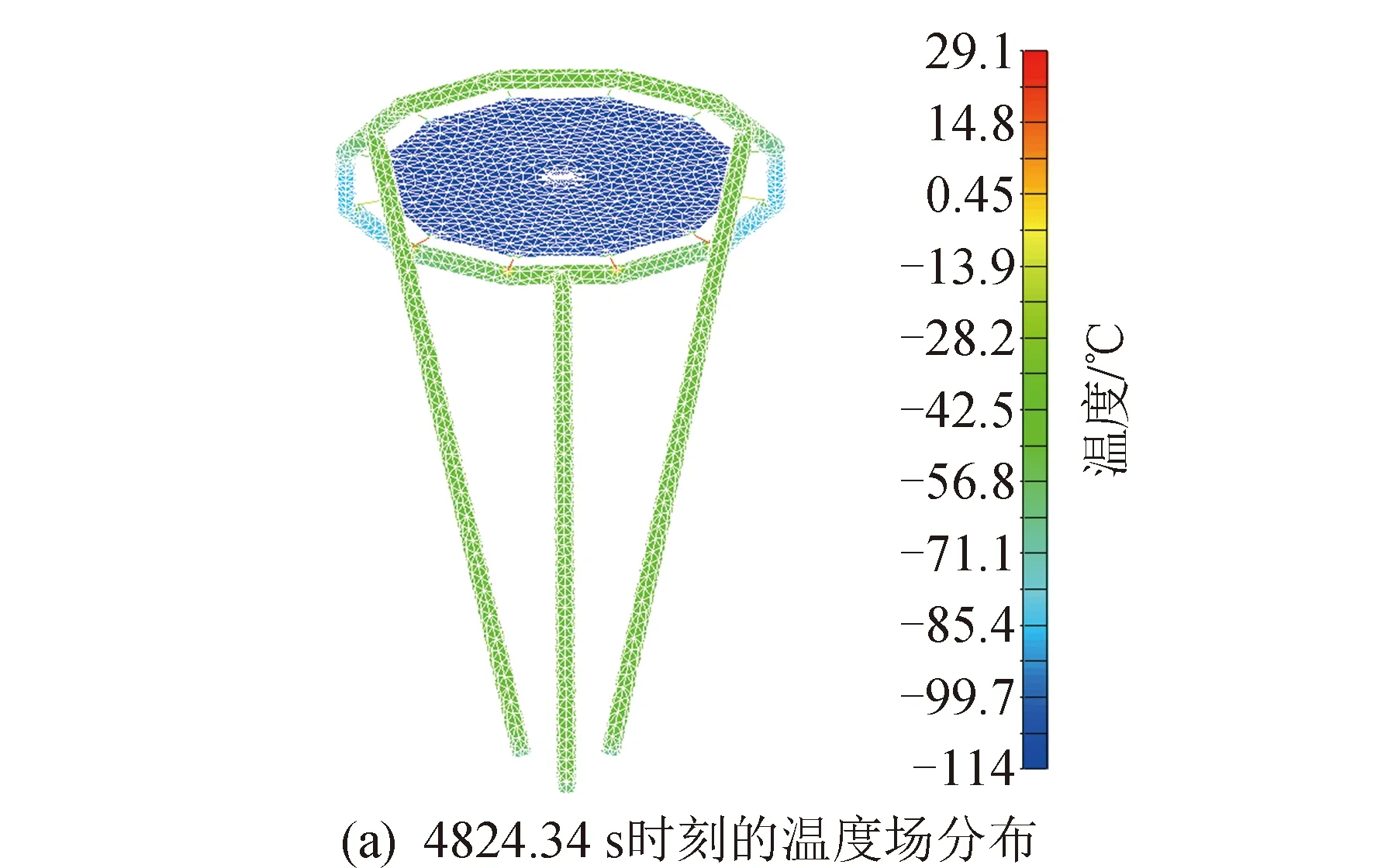
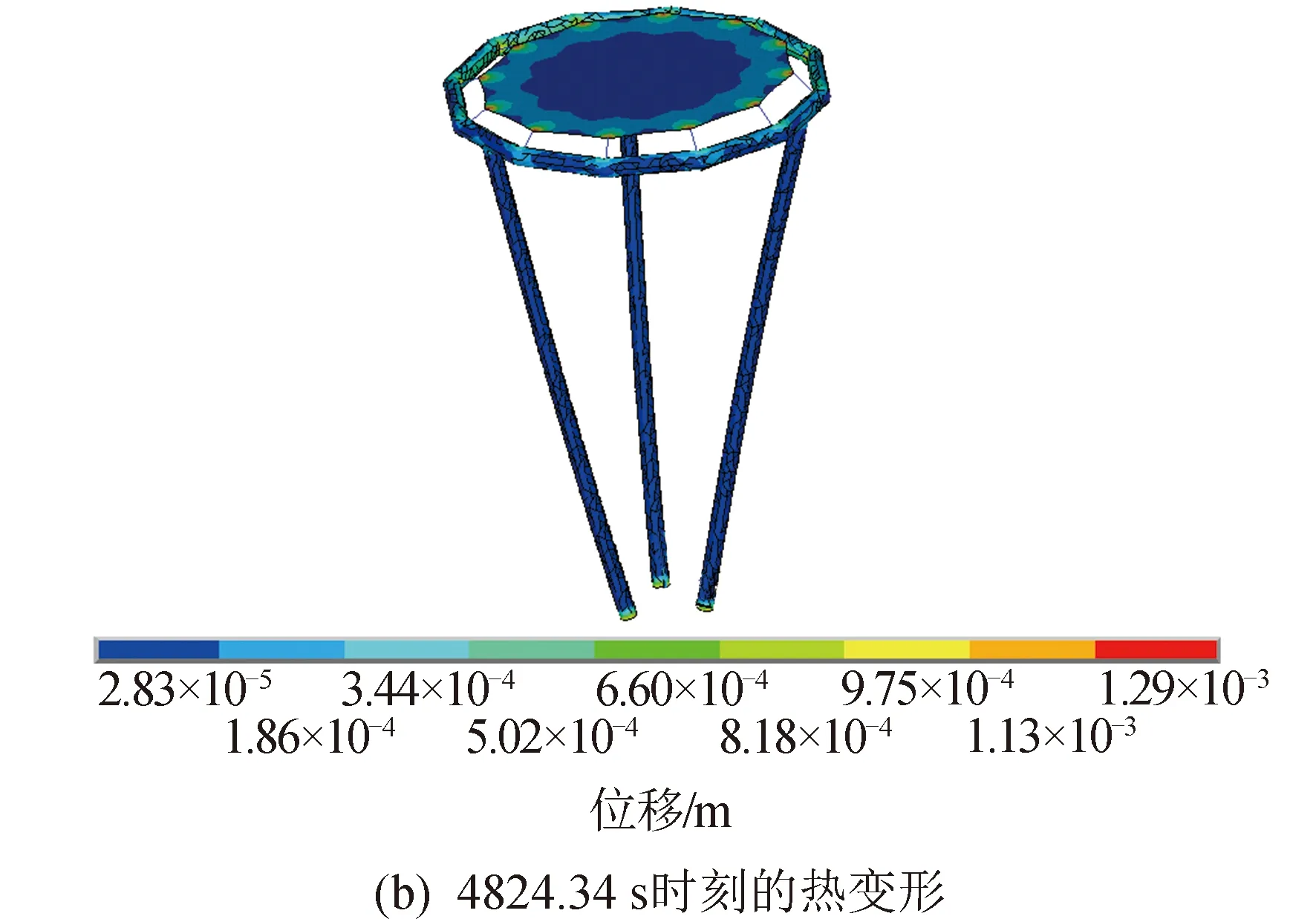
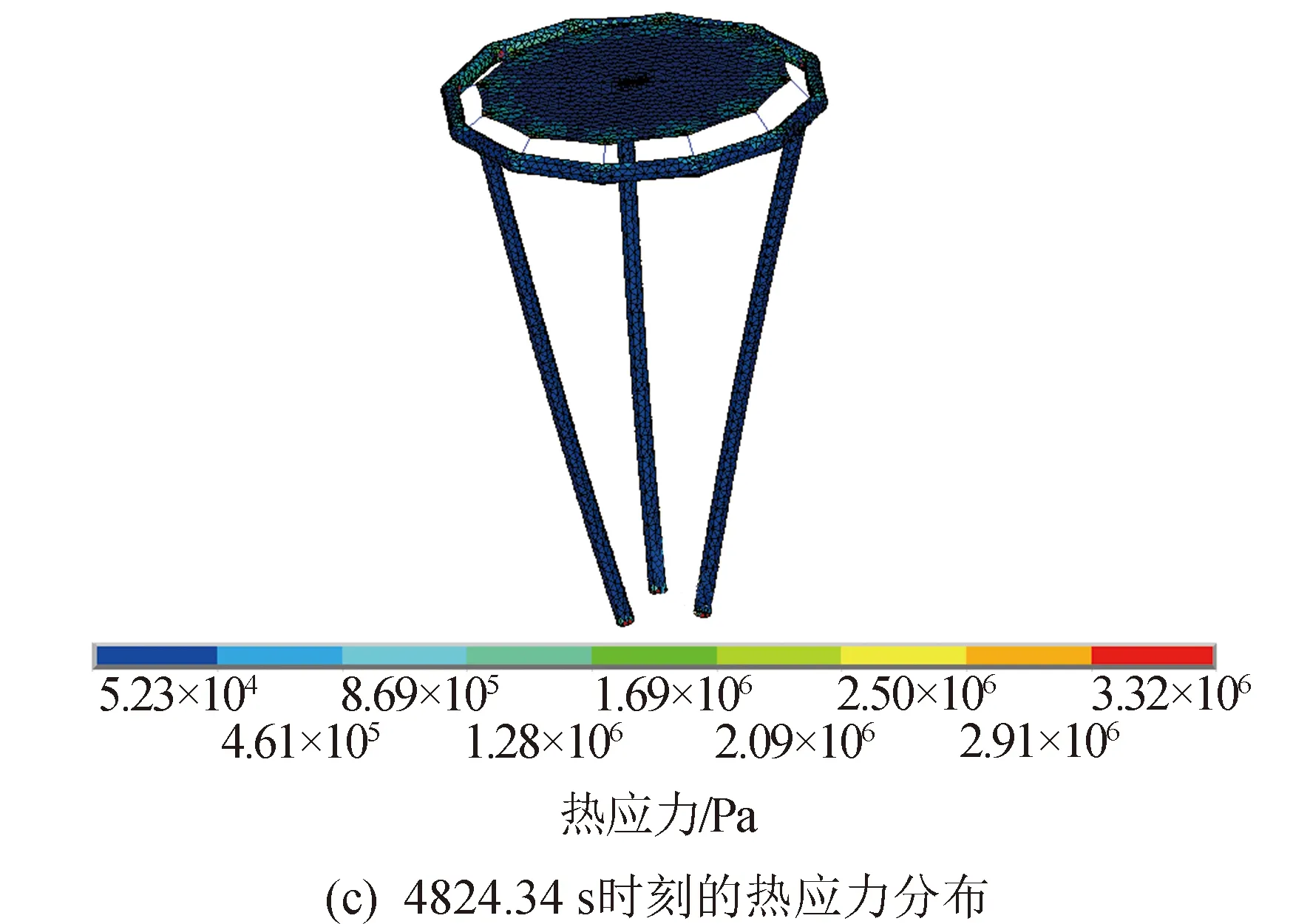
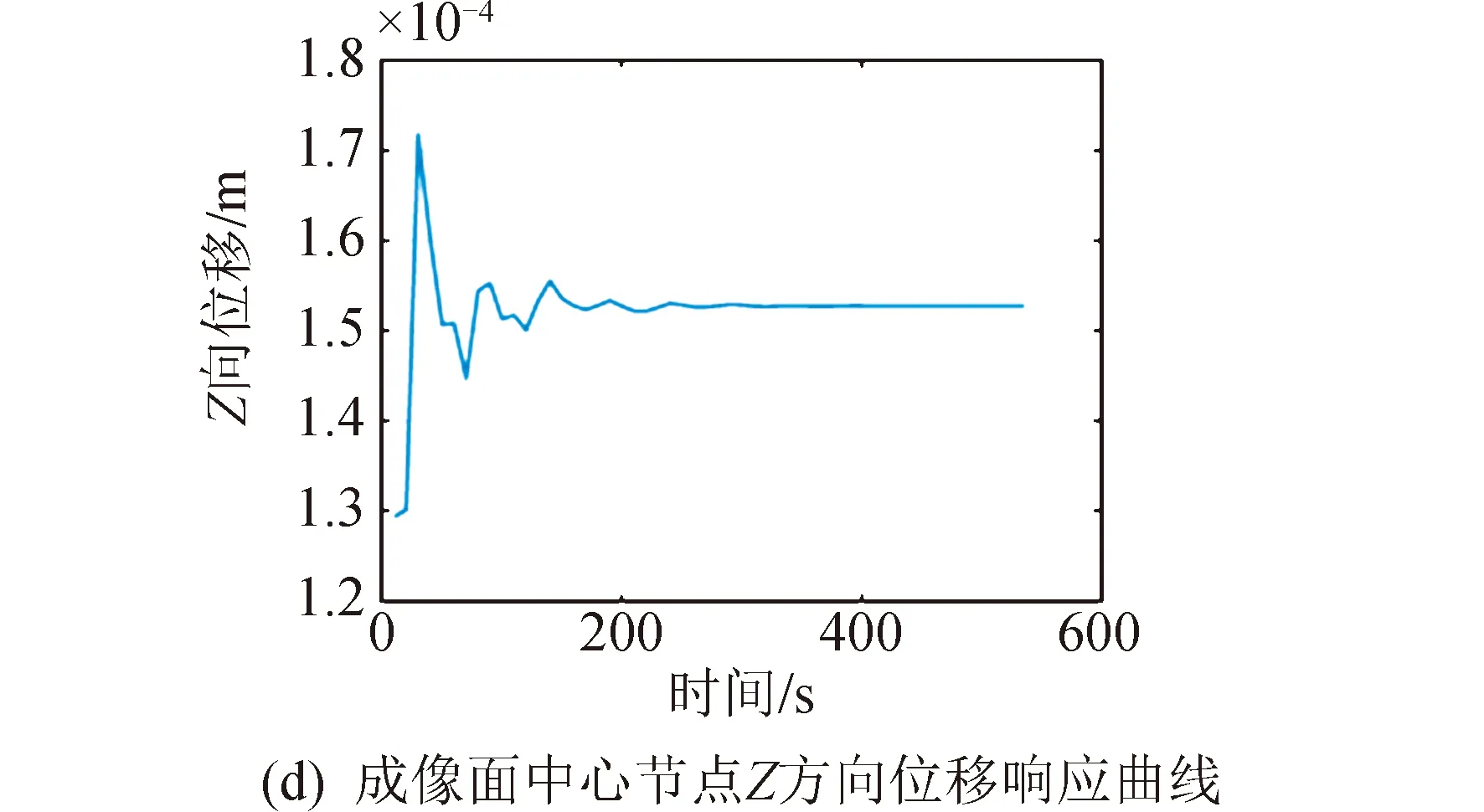
图12 第9个时间步热力耦合分析结果Fig.12 Ninth step thermodynamic coupling analysis results

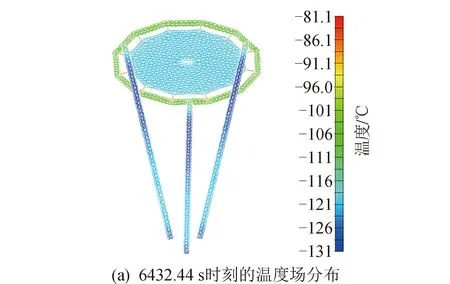
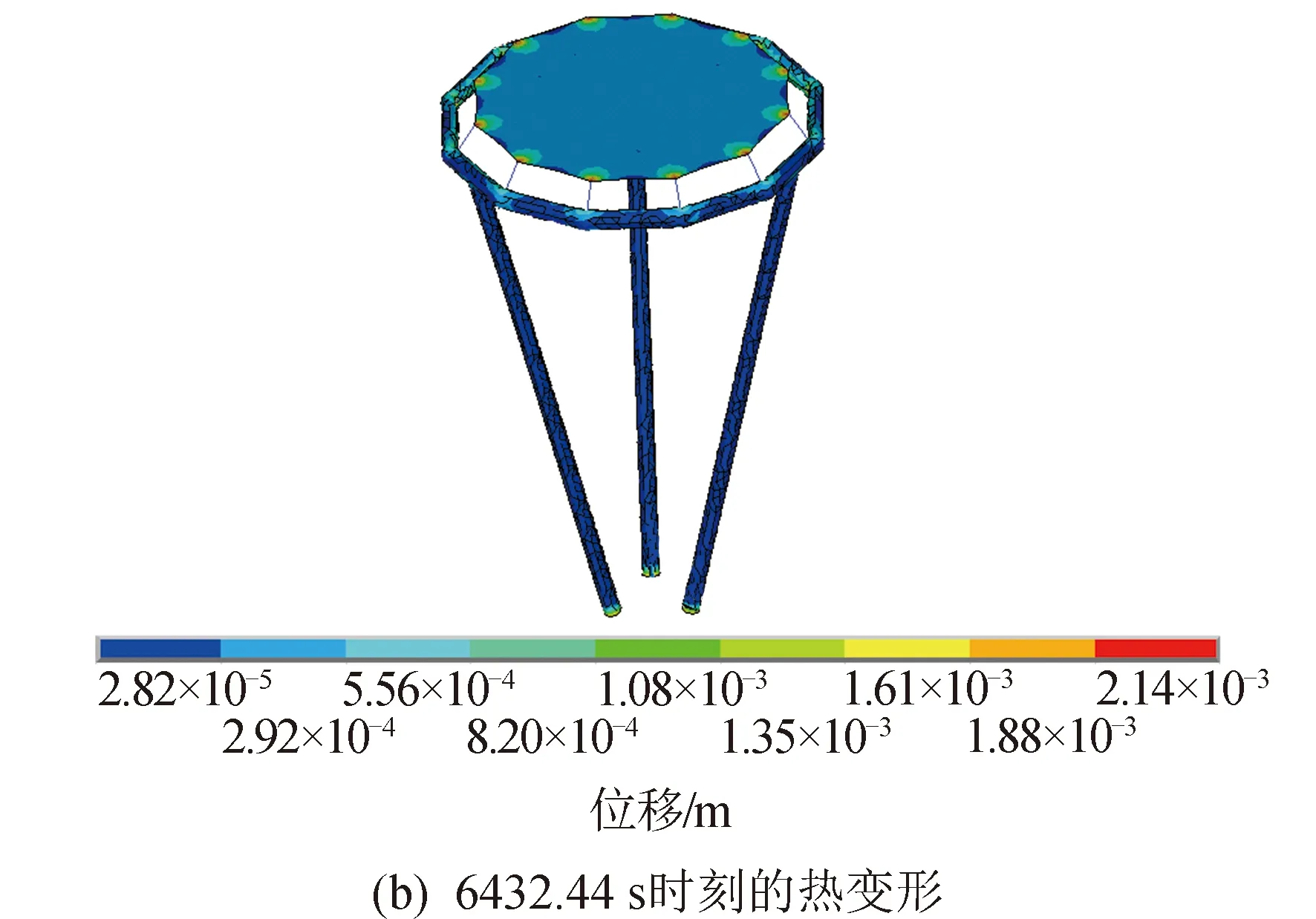
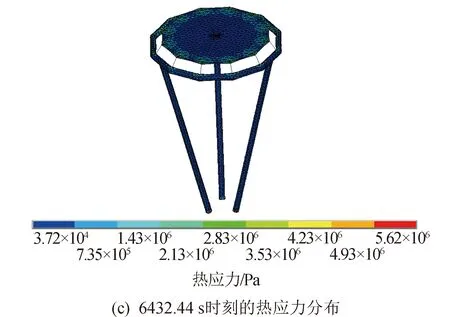
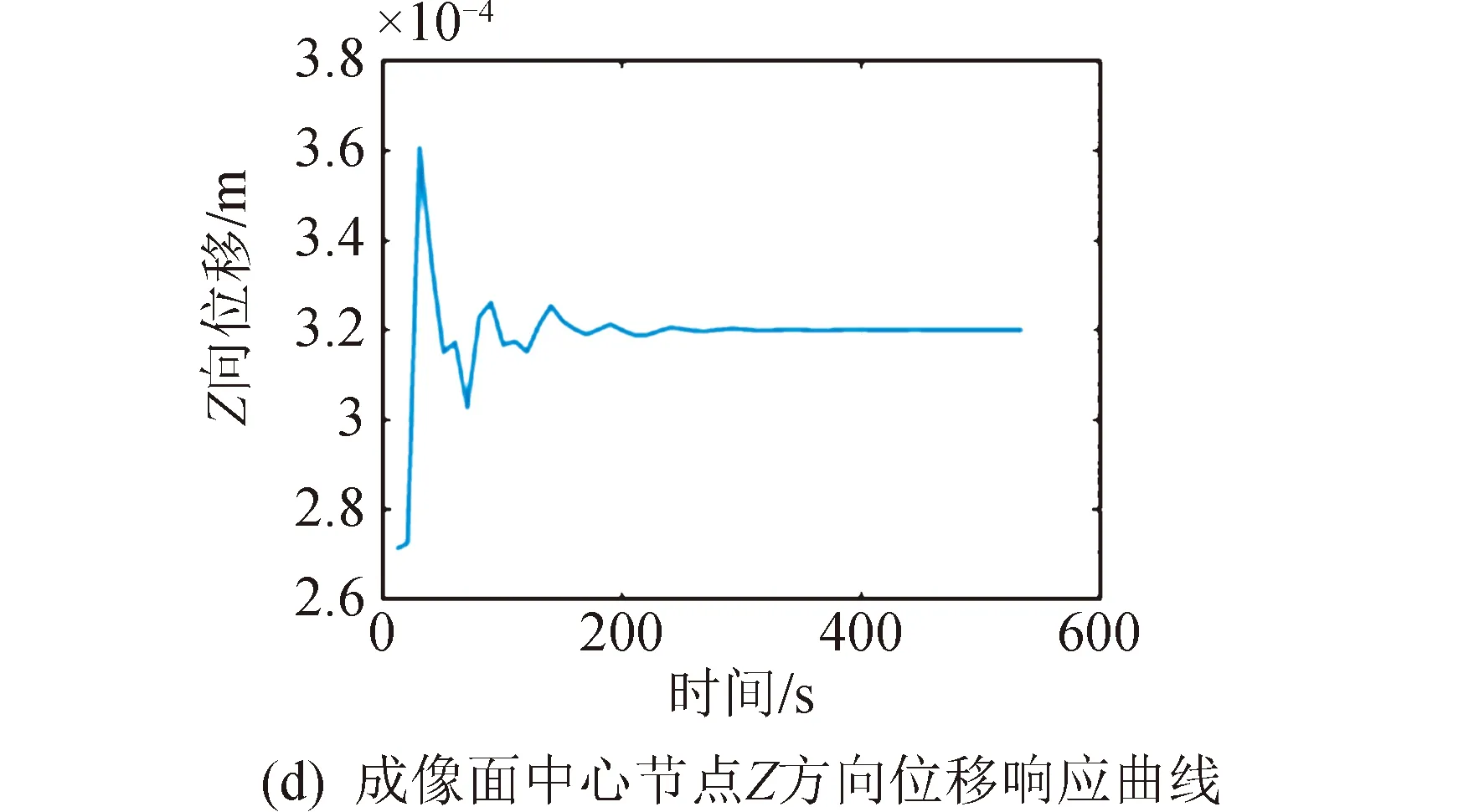
图13 第12个时间步热力耦合分析结果Fig.13 Twelfth step thermodynamic coupling analysis results

由分析结果可知充气薄膜衍射成像展开结构在轨运行时，其温度场分布瞬态变化，表3列出了12个时间步结构上的最高、最低温度值。

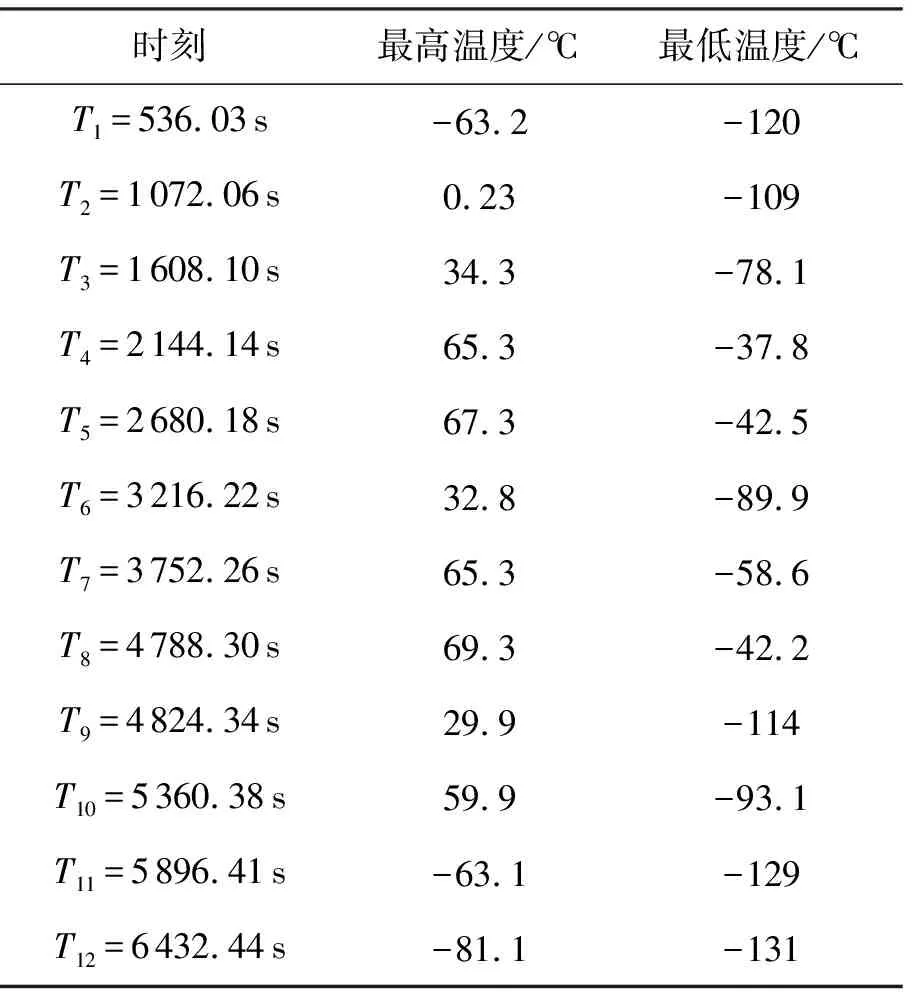
表3 12个时间步结构上的最高、最低温度值

由分析结果可知：最高温度出现在4 788.30 s，为69.3℃，此时结构上最低温度为-42.2℃；最低温度出现在6 432.44 s，为-131℃，此时结构上最高温度为-81.1℃；T10时刻(即5 360.38 s)结构上温度梯度最大，达到153℃，此时充气薄膜衍射成像结构即将进入阴影区，结构上受太阳热辐射情况差异很大，造成结构上较大的温度梯度；T4～T8时刻，衍射主成像面上有明显的局部温度较低区域，主要是充气支撑结构对成像面产生了遮挡影响。

充气薄膜衍射成像展开结构在轨运行过程中，各个时间步中结构的最大热变形值如表4所示。结构最大热变形出现在T2(1 072.06 s)时刻，最大热变形的节点位于充气直管上，达到11.55 mm，此时充气薄膜衍射成像结构刚由阴影区进入日照区，温度场变化剧烈，温度梯度也较大，从而产生了较大热变形。

表5为在轨运行过程中12个时间步充气薄膜衍射成像结构的最大等效热应力。

由此可知最大热应力出现在T12(6 432.44 s)时刻，此时结构上最高温度为-81.1℃，最低温度为-131℃；最大热应力为6.32 MPa，最大热应力节点位于充气直管上，远小于聚酰亚胺薄膜材料的抗拉强度170 MPa，结构满足强度要求。

由各个时间步充气薄膜衍射成像面中心节点Z方向响应曲线可得，成像面中心处没有出现较大的热变形响应。由此可见，空间热载荷主要使充气支撑结构产生了一定的热变形，而对衍射主成像的影响较小。

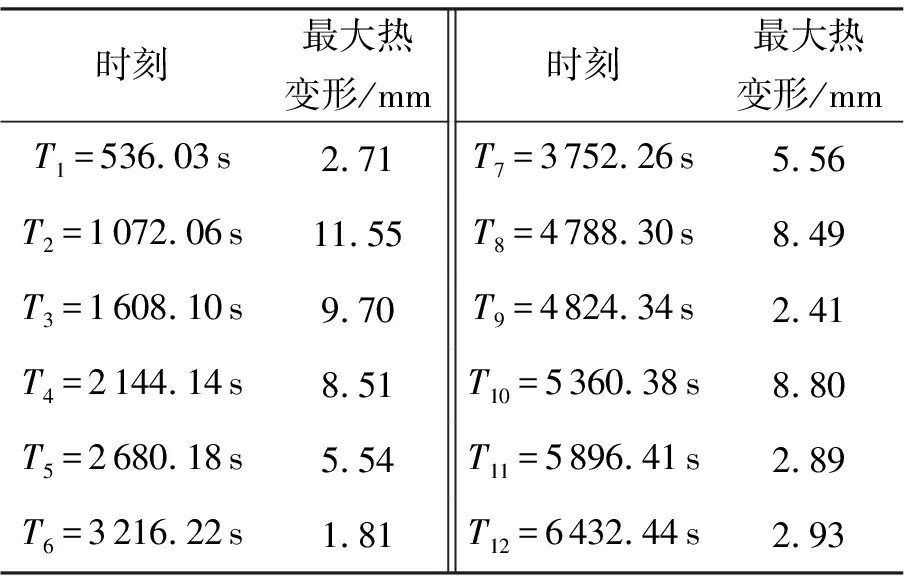
表4 结构最大热变形

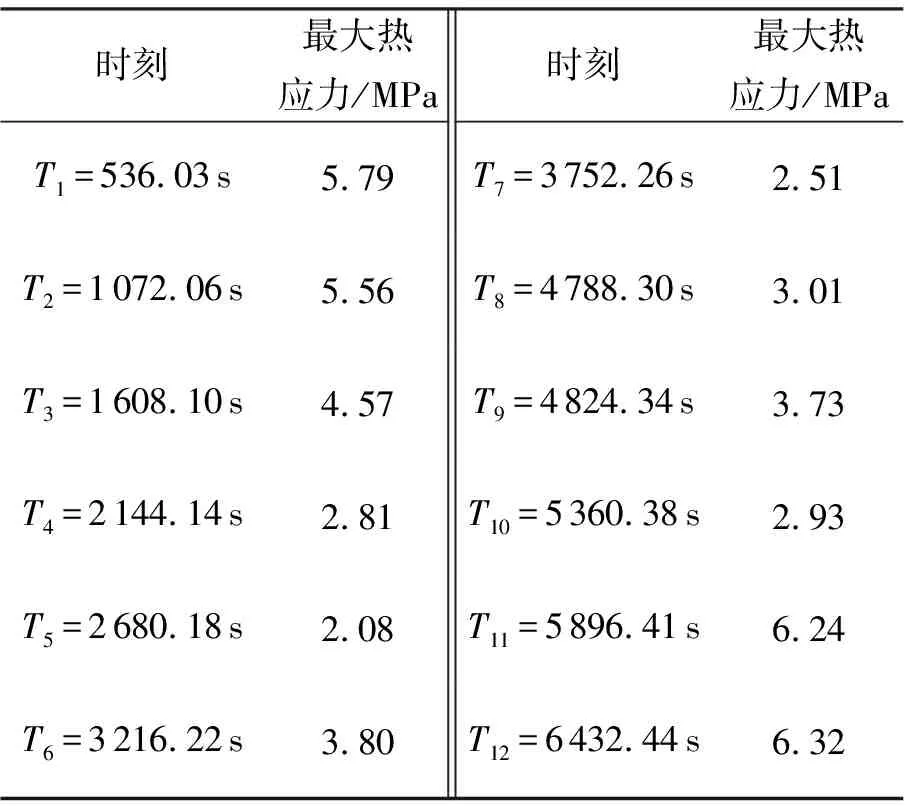
表5 结构的最大等效热应力

5 结束语

本文研究了充气薄膜衍射成像结构的热力耦合效应，采用顺序耦合分析框架，基于I-DEAS和ANSYS二次开发技术，实现了在轨运行一个周期的热力耦合分析，得到了瞬态温度场分布、热变形、热应力响应等，得到以下结论：

1)结构瞬时最高温度为69.3℃，最低温度为-131℃；结构上最大温度梯度达到153℃，此时充气薄膜衍射成像结构即将进入阴影区；T4～T8时刻，衍射主成像面上有明显的局部温度较低区域，主要是充气支撑结构对成像面产生了遮挡影响。

2)充气薄膜衍射成像结构刚由阴影区进入日照区时，结构产生了较大热变形，充气直管上最大位移达到11.55 mm。结构最大热应力为6.32 MPa，远小于聚酰亚胺薄膜材料的抗拉强度。

3)成像面中心处没有出现较大的热变形响应，空间热载荷对衍射主成像的影响较小。

本文的热力耦合分析中假设充气支撑结构中内压保持恒定，这可以通过内压监控系统实现。后续工作可以考虑结构温度场变化引起的内压变化[14]，也可采用充气刚化技术设计充气薄膜成像的支撑结构。