一道质检试题的解析和探究

苏艺伟

(福建省龙海第一中学新校区 363100)

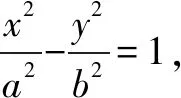
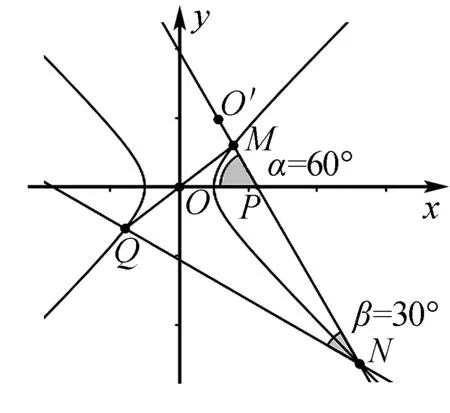
图1

试题分析本题既朴实又创新.朴实之处在于以常见的直线与双曲线相交为载体,结合对称性,考查双曲线中基本量的运算,属于学生熟悉的题型;创新之处在于给出的条件为两个角度,且为倍数关系,让人有一种陌生但是又耳目一新的感觉.看到此试题,觉得有思路可以做,但是细心做下去又觉得有一定的难度,具有一定的挑战性.

解法分析

1.考虑特殊情况

如图1,题目中的点P在x轴上运动,但是具体位置并不知道,这就给题目增加了难度,一时之间感觉难以入手.退一步想,既然点P是动点,那不妨先假设点P就是右焦点.以退为进,看看能否求解.

解析假设点P为双曲线的右焦点,则P(c,0).设M(x1,y1),N(x2,y2),Q(-x1,-y1).

(b2-3a2)2x2+6a2cx-3a2c2-a2b2=0,

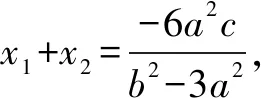
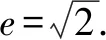
通过上述解题过程,发现对于点P为双曲线右焦点的情况,是可以求出离心率的.而且在(1)式中,c被约掉了,这就引导我们思考:本题的求解跟点P在x轴的具体位置是否无关?

2.考虑一般情况

假设点P(x0,0).设M(x1,y1),N(x2,y2),Q(-x1,-y1).

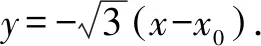
(b2-3a2)2x2+6a2x0x-3a2x02-a2b2=0,

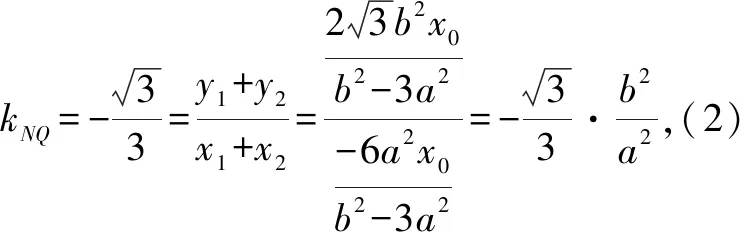
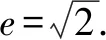
在上述解题过程,发现对于(2)式,x0被约掉了,这就启发我们其实本题的求解跟点P在x轴的具体位置无关.因此,对于本题,采用了特殊化策略,先考虑特殊情况,得到结论,由此受到启发,再考虑一般情况,以退为进.如此一来,化抽象为具体,降低了思维难度,顺利求解.

下面,笔者对此题进行了若干探究.

探究1 是不是当∠MPO=2∠MNQ时,该双曲线都是等轴双曲线?

分析取∠MPO=30°,∠MNQ=15°.假设点P(x0,0).设M(x1,y1),N(x2,y2),Q(-x1,-y1).

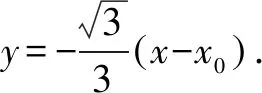
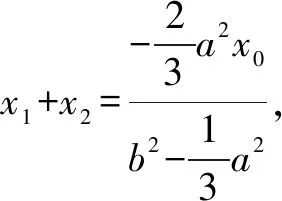
结论1 当∠MPO=2∠MNQ,该双曲线不一定都是等轴双曲线.

探究2 若该曲线为等轴双曲线,则∠MPO=2∠MNQ一定成立吗?

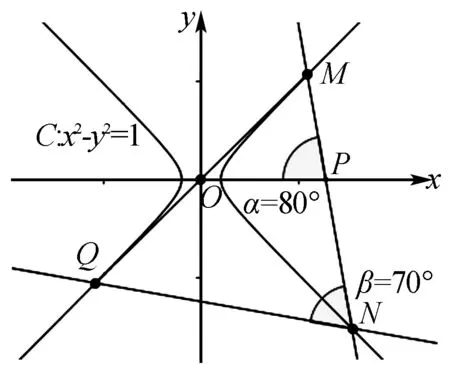
图2

图3

分析借助Geogebra软件进行验证.作出等轴双曲线x2-y2=1,利用定值角度工具作出∠MPO=80°,然后利用角度工具测量出∠MNQ的度数,为70°.再拉动点P,可以发现∠MNQ保持定值70°.对于等轴双曲线x2-y2=4,情况也是一样的.如图2,图3所示.

结论2 若该曲线为等轴双曲线,则∠MPO=2∠MNQ不一定成立.

至此,我们可以清楚地意识到,题目中的条件“若∠MPO=60°,∠MNQ=30°”,通过计算和验证可以得到该双曲线为等轴双曲线,但是并不意味着∠MPO=2∠MNQ与该双曲线是等轴双曲线有必然的关系.题目给出这样的条件其实是降低了试题的难度,因为这两个角都是特殊角,可以计算出正切值.

探究3 当∠MPO=2∠MNQ时,该双曲线的离心率如何求解?

分析不妨设∠MNQ=α,则∠MPO=2α.假设点P(x0,0).设M(x1,y1),N(x2,y2),Q(-x1,-y1).

直线MN方程为y=-tan2α·(x-x0).代入双曲线方程得

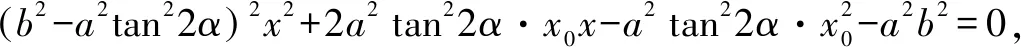
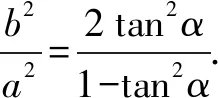
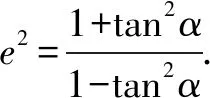
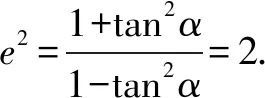
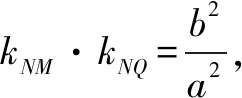
试题变式