高考函数与导数解答题的综合分析

刘耀中 (指导教师：周鹏)

(湖南省衡阳市衡钢中学 421001)

在老师讲解函数和导数综合解析题的过程中，有很多之间的关系都不能够特别的理解，应用起来也不太方便，本文主要是结合学生在高考二轮复习的过程中，通过数次的研究和分析，利用设计问题串的方式解决函数和导数专题的一种比较简便的方法，希望能够帮助到更多的学生解决相应的问题，运用的更加方便快捷.

一、例题分析

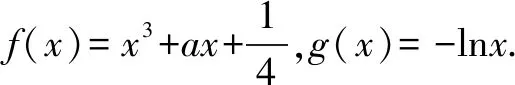
问题一：当a取何值时，x轴为曲线y=f(x)的切线？

问题二：用min(m,n)表示m,n当中的最小值，设函数h(x)=min{f(x)，g(x)}(x>0)，讨论h(x)零点的个数.

首先对题目进行分析，在本道例题当中需要考察的主要是三次函数和对数函数的问题，涉及到主要的知识点有切线、最值和零点问题，除此之外还有参数、新定义问题，尤其是第二个问题，需要涉及到的数学知识点比较多，也比较复杂，因此我们需要先设计问题串，就是说搭建解析的支架，这样解析相对来说也就比较简单了.

二、设计问题串

问题串是方便我们去理解和解析问题的，因此设计的时候要逐渐的加深，从简单的问题向复杂的问题引入.

问题一：比如说从函数y=f(x)的零点方程推算出函数方程的图象和x轴的交点坐标，与函数g(x)交点的横坐标.这样问题的设计能够将原本的问题转化为方程的根进行解析.

问题二：根据上述的题目我们已经知道min(m,n)表示m,n当中的最小值，所以将

h(x)=min{x+1，-lnx}(x>0)的图象画出来，并且计算出h(x)的零点的个数.这个问题可以充分的理解min(m,n)是什么意思？然后用数形结合的思想解析函数的零点问题.

问题三：分析函数f(x)=ax3+bx2+cx+d(a≠0)的性质和图象.

比如说当a>0的时候，三次函数的图象大致是什么样子的？当a<0的时候，三次函数的图象又是什么样子的？三次函数如果有极值点的化，极值点的个数会有两个，如果三次函数的定义域为R，那么零点至少应该有1个，最多不能超过3个.这个问题会让我们对图象做到足够的了解和熟悉，为三次函数的零点求解做出铺垫.

三、例题解析

在解析之前我们要清楚函数h(x)的零点等价于哪一个函数区间的零点，通过这个问题我们就能找到h(x)零点问题的突破口.

第一种情况，当a≥0时，f′(x)=3x2+a>0，并且x∈(0,+)恒成立，

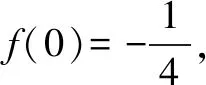
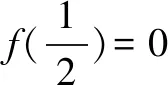
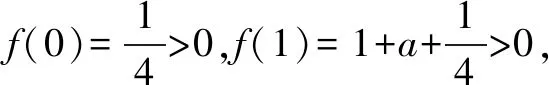
可以得出函数h(x)的零点个数为1个.

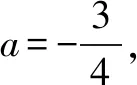
在上述解题的过程中，首先对题目进行了分析，就像是我们平常在考试的时候拿到试卷要先审题，了解在题目中给出的条件以及需要考查的是什么问题，当把这个问题了解清楚之后，再去解题就会容易很多.然后再根据题目的意思列出解题的思路，就是在上述的过程中我们用到的设计问题串，从上述可以看到：问题是按照难易的层次逐渐递进的，根据解题的思路将设计的问题一步步的解决，为最后的解析过程做一个很好的铺垫，最后的问题也就迎刃而解了.无论是老师们在讲解的过程中，还是我们自己在解题的过程中，关于数学的问题相对来说都是比较抽象的，因此要掌握图象运用的方法，在解题的过程中多次进行画图的测试，图象能够将抽象的数学知识和概念呈现出来，再去解题的时候相对来说就比较容易了，在一定程度上降低了问题的难度.就像在上述的过程中，通过对a的六种情况的分析，将函数h(x)的零点个数逐渐的求解出来，这也是一个解题的策略，对参数的范围进行讨论，要保证不重不漏，这样的话就会让整道题变得简洁明了，便于实质性的操作，对我们以后在模拟和高考中都有很大的帮助.