离心率解法探究——以2019年全国高考Ⅰ卷数学理科第16题为例

徐 健

(新疆教育科学研究院 830092)

2019年数学高考已经尘埃落定，学生反映有些题不好做，题目难度有点“大”.事实上可能是解题方法选择不恰当，或者没有把握问题的本质造成的，而不是题目太难.以全国Ⅰ卷理科第16题(压轴题)为例，仔细研究发现，本题非常精致.若死做，运算繁琐；若理顺题设的几何关系，找出背后的数量关系，此题非常漂亮，入口宽阔，运算量小，具有很好的区分度.现将九种解法总结于此，以飨读者.

一、试题呈现

二、总体分析

本题依托平面向量给出中点和直线与直线等位置关系，以离心率为出口，借助渐近线对双曲线的一些几何特征进行考查.其间把直线方程、直线的平行关系、垂直关系、直线的斜率、直角三角形面积、直角三角形的几何特征、等边三角形、轴对称问题、圆的方程进行了深刻全面的考查.在逻辑推理中运算，在计算中揭示本质，而非死算到底.实属一道难得的好题，可以作为教学的典型例题，全方位提升学生核心素养，避开所谓的刷题“赢”高考.

三、解法探究

分析1以面积为突破口.如图1，由已知容易得到直线F2B和OB的方程，从而解出点B的坐标.在△BF1F2中，利用等面积法可以建立a，c的关系式，求得离心率.

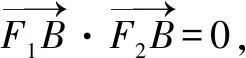
整理得c2=4a2，解得e=2.

分析2 以直角三角形性质为突破口.由直线OB，F2B的斜率可以发现相关倾斜角的关系，从而得到相关三角形边的关系，建立a，c的关系式，求得离心率.

分析3 以正三角形的性质为突破口.进一步分析△BOF2发现，△BOF2是等边三角形.利用倾斜角和斜率的关系，建立a，c的关系式，求得离心率.

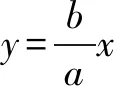
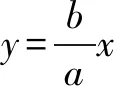
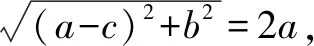
分析5 以坐标为突破口.由解法1和解法4得到点B的坐标的两种形式，横纵坐标分别相等可以建立a，c的关系式，求得离心率.

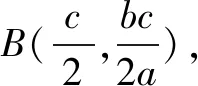
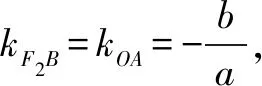
分析7以轴对称为突破口.直线OA是线段F1B的垂直平分线.利用这个性质也可以建立a，c的关系式，求得离心率.

(同理，从|BF1|=2b，|BF2|=2a也可以解得e=2.)

分析9 以角度为突破口.分析△BF1F2的特征，能够发现△BF1F2是一个最常见特殊直角三角形，也可以建立a，c的关系，求得离心率.

解法9 因为△BF1F2是直角三角形，△BOF2是正三角形，所以∠BF1F2=30°.

整理得3b2=(a+c)2，解得e=2.

四、解法提炼

本题表象上是一个双曲线问题，解题过程中若始终围绕双曲线思考可能就会陷入困境.不得不感叹命题专家的高明，纵观全卷，似乎没有考查直线和圆的题目，难到这些知识不重要吗？经过本题的研究才发现，关于直线和圆的知识进行了全面、隐蔽、深刻的考查，其能力要求达到了应用层次.换句话说，只有学通学活直线和圆，才能运用到双曲线中去灵活解决实际问题.

求离心率是解析几何中一个常见的重要的问题.解析几何本质还是几何，在解题过程中要充分利用题目隐含的几何关系，这样可以大大减少运算量.解析几何又是依托代数开展研究的，因此解题中又必须全面关注题目中的相关代数知识，本题中直线方程、直线的斜率、圆的方程、等边三角形、直角三角形等起了重要作用，为建立a，c的关系式奠定了广泛的基础.视角很关键，也就是切入点，从长度、角度、面积、斜率、对称等方向分析问题，让思路变得开阔，思路间还相互补充，让题面变得清澈见底，直至问题的源头，△BF1F2是内角为30°，60°，90°的最常见直角三角形.可见专家命题的出发点非常朴素，在简单中创造神奇，体现了创新无处不在的生活哲理.有意思的是，本题产生了解法族群，依托长度、角度、斜率均得到了几种解法，让解题变成一种享受.当然各种解法尚有运算量的区别，在考试时需要甄别选用，确保又快又对，前文有几种解法简直可以口算得答案，在正确思维的引领下，这能算难题吗？几何位置关系对减少运算和建立等式至关重要，在学习和解题中务必用心体会这一点.

离心率的问题通常有两种，一种是求值，一种是求范围.求值的方法有：

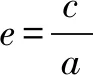
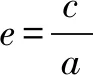
(3)利用离心率的定义和圆锥曲线的定义求解；

(4)利用几何关系求解；

(5)利用圆锥曲线的统一定义求解.

求范围通常是建立关于e的不等式，求e的范围，此类问题需建立不等式，往往更难.

求离心率的问题是一个综合问题，牵涉的面比较广，用到的知识比较多，可用的技巧也丰富，教无定法，学无诀窍，我们只有多思考，多总结，多实战，方可做到得心应手.

五、教学启示

因此，高中数学教学应主动探索知识内容背后的数学思想和方法，重视数学思想和方法的教学与实践.数学解题教学要突出“想”的训练，“想”到位了，算就少了.数学教学还要重视思维能力和创新意识的培养，否则具有高阶思维的题目学生还是一筹莫展.