险入误区化惑为笃——对一道颇为流行试题解法的商榷

廖达凡 朱 华

(1.江西省大余中学 341500；2.江西省赣州市大余县教学研究室 341500)

有这样一道颇为流行的试题：

已知抛物线C:y2=x上一 定点B(1,1)，P、Q是抛物线上的两个动点，当动点P在抛物线上运动时，BP⊥PQ，则点Q的纵坐标的取值范围是____．

课堂教学中，笔者给出了如下解答过程：

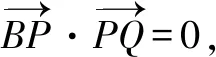
问题进行到这里时，笔者以为这道试题已经处理得很完美．这时候，有学生突然对上述解答提出疑问，需要对答案进行修正，理由是：

学生对问题解答的修正，表面上看起来使答案更加合理、严谨些.

课后，笔者带着困惑查阅了目前部分教辅资料和试卷，发现的确有相当一部分答案是流行后者答案，那究竟哪个答案是正确的呢？

笔者对这道看似“错误答案”的试题进行自觉分析，从险入误区，到不断推敲其答案的合理性，最终找到解题思维的愚蠢点，转隐为显，化惑为笃，回归问题本质.可以说，这是一道十分容易答错的试题，学生需要具备良好的思维品质和解题素养以及敏捷的判断分析能力来完成问题的解答.