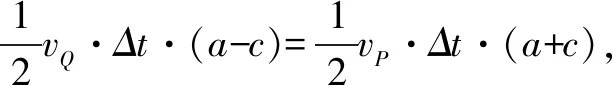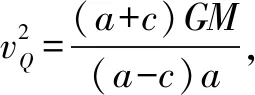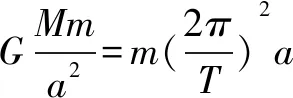数学搭桥物理 巧求椭圆面积

张克磊 方 林

(1.安徽省定远县第二中学 233200;2.安徽省巢湖市第四中学 238000)

常言道：“数理不分家”, 数学与物理是联系紧密的两门学科，数学是物理解题的工具，物理又可以使数学知识得到运用.在高中物理竞赛中有很多试题涉及到圆锥曲线知识，需要考生掌握一定的数学知识，如2018年度全国高中应用物理竞赛中就出现了运用椭圆面积求做功的试题，椭圆面积如何求解，仅数学方法有多种，本文将分别从数学和物理两个角度推导椭圆的面积，为师生提供参考.

解法一 数学方法之积分法

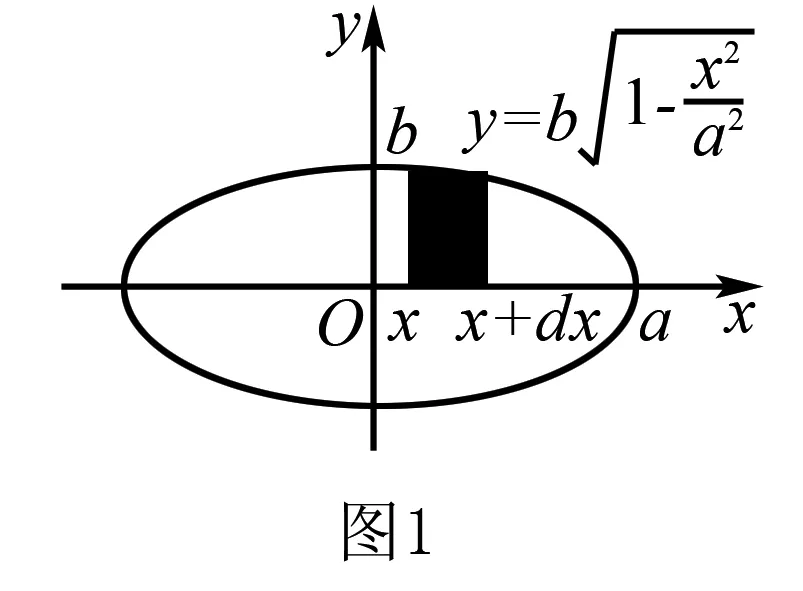
根据椭圆图形的对称性可知，整个椭圆的面积应等于位于第一象限内图形面积的4倍.

如图1所示，取x为积分变量，由题意知0≤x≤a，

解法二 数学方法之射影法

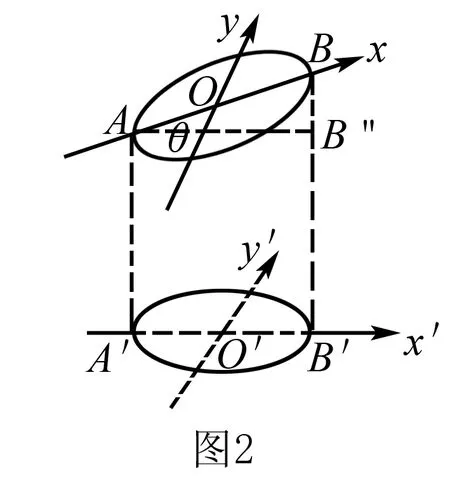
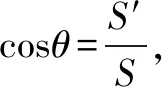
解法三 物理方法之开普勒定律结合机械能守恒定律

如图3所示，P、Q两点为行星运动的椭圆轨道的远地点和近地点，F为椭圆焦点(与太阳中心重合)，设轨道的半长轴为a、半短轴为b、焦距为c，设vP、vQ分别表示卫星在这两点的速度，由开普勒第二定律可知卫星和地球的连线在相等的时间内扫过的面积相等，取极短的时间Δt，则有