设元需讲究 运算更简捷——抛物线中的设元探究

蔡 明

(浙江省诸暨市浬浦中学 311824)

解析几何的学习过程中，往往设一个或多个未知量，但是很多题里消来消去运算繁琐，因此在解析几何中因所设元的影响，对其运算带来困难或运算量较大.在解析几何教学中，总感觉到学生遇到解析几何题目时还是无从下手，本文利用抛物线为载体，运用设点为元，简化解题.

例1设A,B为抛物线y2=2px(p>0)上的点，且满足OA⊥OB(O为坐标原点)，求证：直线AB过定点，并求出这个定点的坐标.

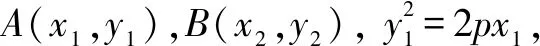
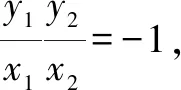
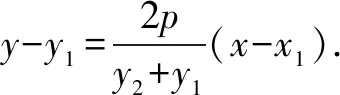
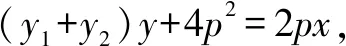
易得直线AB过定点(2p,0).

建立方程组求解是解析几何的通法，上述解法虽脱离基本做法，但解题也清楚、简洁.本题通过对曲线上点运用坐标进行转化，体现解析几何的本质：运用坐标处理问题.

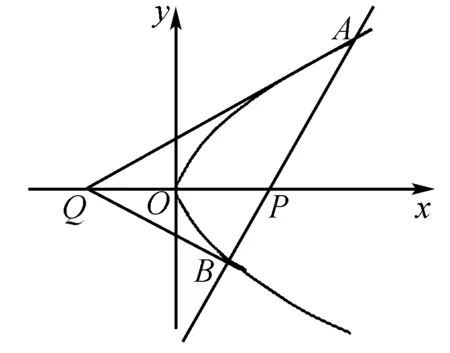
图1

例2如图1，已知不垂直于x轴的动直线l交抛物线y2=2mx(m>0)于A,B两点，若A,B两点满足∠AQO=∠BQO，其中Q(-a,0)(a>0)，O为坐标原点，求证直线AB过定点.

分析本题涉及的点、直线比较多，导致设法混乱，出现多元情形.加之题目本身又含有变量，基本方法运算量较大.

整理得t1t2+2ma=0.

故从AB的方程可以看出，直线过定点(a,0).

例3已知抛物线y2=2px(p>0)上一点A(a,b),(a≠0)作倾斜角互补的两条直线AB,AC，点B,C也在抛物线上，求证：直线BC的斜率为定值.

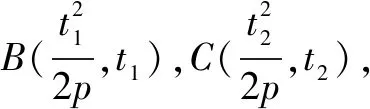
由于直线BC的斜率为

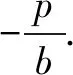
上述两题的做法充分避开多元问题，在解法上如出一辙，也是解析几何中抛物线上与点有关的常用做法.

图2

例4如图2，由半圆x2+y2=1(y≤0)和部分抛物线y=a(x2-1)(y≥0，a>0)合成的曲线C称为“羽毛球形线”，且曲线C经过点(2,3).

智慧水务战略是水务公司转型发展的重要动力，在战略顶层设计中需要水务公司高层的大力支持，在战略实施中也为水务公司带来了实实在在的运营管理水平提升，解决了企业在人力、流程、财务、客户服务等方面存在的若干管理问题和漏洞，未来将进一步为企业创新发展提供更加坚实的基础支撑平台。

(1)求a的值；

(2)设A(1,0),B(-1,0)，过A且斜率为k的直线l与“羽毛球形线”相交于P,A,Q三点，问是否存

在实数k，使得∠QBA=∠PBA？若存在，求出k的值；若不存在，请说明理由．

分析本题若理清思路不难发现，解题的关键是与点Q有关，因此只需用Q的坐标解题即可.

解(1)把点(2,3)代入y=a(x2-1)得3=a·(22-1)，所以a=1．

(2)由题意可知∠QBA=∠PBA，∠APB=90°，则∠QBA+∠BAP=90°，故kQB·kQA=1．

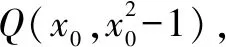
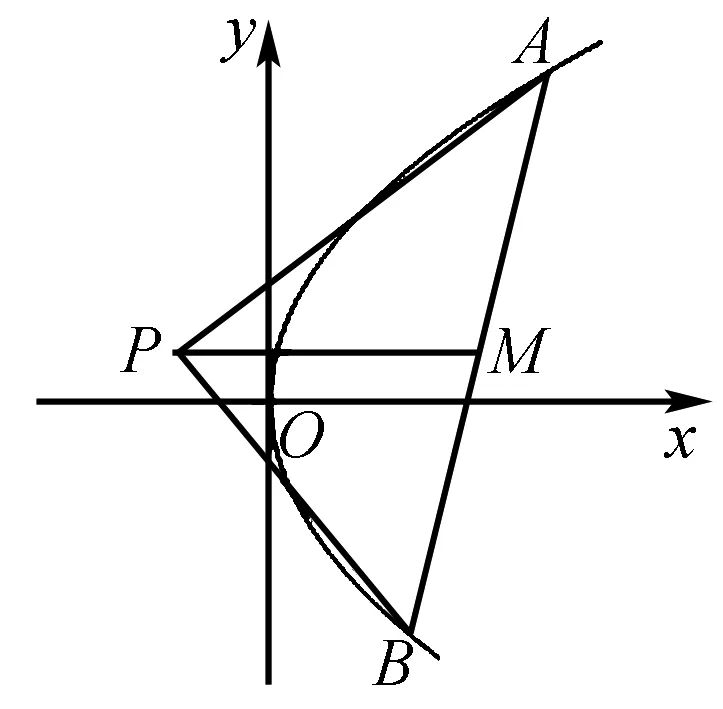
图3

例5如图3，已知点P是y轴左侧(不含y轴)一点，抛物线C:y2=4x上存在不同的两点A,B，满足PA,PB的中点均在抛物线C上．

(1)设AB中点为M，证明：PM垂直于y轴；

分析此题有一定的难度，若盲目地运用直线方程会使消元带来困惑，结合条件，不难发现问题都与坐标有关，因此直接设点会有不错的效果.

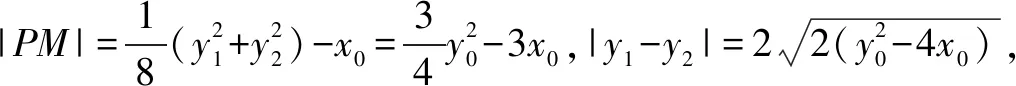
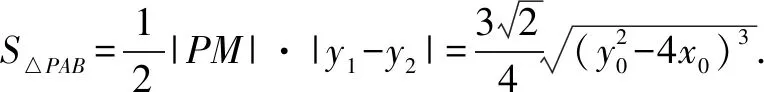
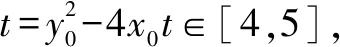
求范围问题，往往利用条件转化为一元函数问题，将多元问题转化为一元问题，再结合函数，选用恰当方法求取值范围，本题正是利用二次函数在区间上的取值，利用复合型函数的单调性确定范围.

结合以上几例可以发现，在抛物线上与点相关的问题往往采用点坐标计算，比用直线、抛物线方程组的方法求解来的更简单，相对而言涉及元也比较少，为解题带来方便.平时多对试题探究，从中寻找某些解题规律，这样才能以不变应万变.