总量生产函数的恒等式性质——兼论全要素生产率的实际含义

谢富胜 张天啸 张俊夫

一、引言

全要素生产率(Total Factor Productivity，简称TFP)表示资本和劳动力等有形投入之外，其他所有影响产出的要素贡献，全要素生产率常常被视为代表技术进步或效率改进的变量，学术界对于全要素生产率代表的具体含义虽存在不同观点，但均认为全要素生产率是影响生产的重要因素。然而，绝大多数全要素生产率的估算都不能完全离开总量生产函数，对总量生产函数的质疑与批评一直存在，因此测算的全要素生产率的实际含义始终存疑。在“两个剑桥之争”中，斯拉法、琼·罗宾逊等都围绕异质性资本对总量生产函数进行批评，其中资本衡量的循环论证、资本反转等问题俱已严重动摇了总量生产函数的根基。对生产函数最关键的批判来自谢克提出的收入恒等式问题，即总量生产函数来源于收入等于利润加工资的恒等式变形，不能表示实际的生产过程。(1)Shaikh,A.“Laws of Production and Laws of Algebra:The Humbug Production Function”.Review of Economics and Statistics,1974,56(1):115-120.这一批评指出基于总量生产函数的全要素生产率与技术没有直接关联。费利普和马克比在谢克研究的基础上，通过经验数据的检验，进一步证明了基于总量生产函数得到的全要素生产率只是工资率和利润率的函数，并不能表示生产因素。(2)Felipe,J.,and J.S.L.McCombie.“Methodological Problems with Neoclassical Analyses of the East Asian Miracle”.Cambridge Journal of Economics,2003,54(5):695-721.

然而，这一批评却未能得到学界承认。经济学者受工具主义方法论的影响，新古典总量生产函数仍因其在经验研究中的广泛应用而得到拥护。(3)Ferguson,C.E.,and R.F.Allen.“Factor Prices,Commodity Prices,and Switches of Technique”.Economic Inquiry,1970,8(2):95-109；Wan,H.Y.Economic Growth.New York:Harcourt Brace Jovanovich,1971.萨缪尔森与西蒙等虽然都认识到总量生产函数与恒等式之间的关联，却均未提及谢克的批评，他们只是止步于怀疑而未能揭示总量生产函数的本质。(4)Samuelson,P.A.“Paul Douglas’s Measurement of Production Functions and Marginal Productivities”.Journal of Political Economy,1979,87(5):923-939；Simon,H.A.“On Parsimonious Explanations of Production Relations”.Scandinavian Journal of Economics,1979,81(4):459-474.索洛虽然讨论过收入恒等式问题(5)Solow,R.M.“Second Thoughts on Growth Theory”.In Steinherr,A.,and D.Weiserbs (eds.).Employment and Growth:Issues for the 1980s. Dordrecht:Martinus Nijhoff,1987.，却未能把握收入恒等式问题的要点。即使谢克、费利普、马克比等人已经进行了大量相关研究，但总量生产函数和全要素生产率仍被广泛使用。

一些经验事实也挑战了全要素生产率的解释力。比如在针对“亚洲四小龙”的研究中，相关文献就指出，“亚洲四小龙”在高速经济增长时期的全要素生产率的增长率并未显著高于发展中国家，其中新加坡在20世纪60年代中期之后甚至经历了全要素生产率的零增长。(6)Young,A.“A Tale of two Cities:Factor Accumulation and Technical Change in Hong Kong and Singapore”.NBER Macroeconomics Annual, 1992,7:13-63.这不仅有悖常识，也与“亚洲四小龙”的实际发展情况不符，一些基于微观的企业数据的研究就表明“亚洲四小龙”在高速增长时期存在着可观的技术创新与吸收过程(7)Felipe,J.“Total Factor Productivity Growth in East Asia:A Critical Survey”.Journal of Development Studies,1999,35:1-41.，得出违背事实的结果源于全要素生产率的计算问题。如果能明确总量生产函数的恒等式性质，类似新加坡全要素生产率增长率为零的情况就可得到更为合理的解释。如费利普和马克比所述，由总量生产函数得到的全要素生产率只是利润率、工资率与利润份额的函数，因此新加坡全要素生产率的零增长率可能只反映了收入分配方面的某种特定情况，取决于总量生产函数的参数设定，并不能说明其没有技术进步。(8)Felipe,J.,and J.S.L.McCombie.“Methodological Problems with Neoclassical Analyses of the East Asian Miracle”.Cambridge Journal of Economics,2003,54(5):695-721.

全要素生产率近年来已成为国内经济学界研究的热门专题，总量生产函数的恒等式性质所造成的影响就更加不容忽视。本文在谢克、费利普、马克比等人相关工作的基础上，基于收入恒等式构造不同形式总量生产函数的一般方法；对基于收入恒等式测算全要素生产率的多种方法进行分析，说明了全要素生产率的实际含义，我们的分析表明用全要素生产率来代表技术进步或效率改进是不恰当的。使用中国1993—2016年的宏观经济数据，我们检验了索洛残差法估算的全要素生产率的实际含义。

二、文献综述：总量生产函数与收入恒等式的联系

(一)柯布-道格拉斯总量生产函数与收入恒等式的关系

柯布和道格拉斯首先估计了之后被称为“柯布-道格拉斯(C-D)”形式的总量生产函数，得到了较好的拟合结果。(9)Cobb,C.W.,and P.H.Douglas.“A Theory of Production”.American Economic Review (Supplement),1928,18(1):139-165.与经验数据的良好契合使得C-D生产函数常被认为能够反映经济体的实际生产情况，因而在此后的经济研究中得以大量运用。同时，估计得到的资本弹性非常接近于利润份额，这也被认为是对边际生产力理论的有力证据。阿罗更是认为柯布和道格拉斯的《生产理论》一文是《美国经济评论》此前百年内最出色的二十篇论文之一。(10)Arrow,K.J.,Bernheim,B.D.,Feldstein,M.S.,McFadden,D.L.,Poterba,J.M.,and R.M.Solow.“100 Years of the American Economic Review:The Top 20 Articles”.American Economic Review,2011,101(1):1-8.

C-D形式的总量生产函数在被广泛运用的同时也受到质疑，一部分学者已经触及总量生产函数背后的收入恒等式。布朗就曾指出C-D生产函数中的资本与劳动的弹性和利润与工资的份额只是一枚硬币的两面，不能说明边际生产力理论是正确的。(11)Phelps Brown,E.H.“The Meaning of the Fitted Cobb-Douglas Function”.Quarterly Journal of Economics,1957,71(4):546-560.西蒙和莱维通过同时求得C-D生产函数和收入恒等式的一阶泰勒近似式，发现资本与劳动的弹性正好等于利润与工资的份额。(12)Simon,H.A.,and F.K.Levy.“A Note on the Cobb-Douglas Function”.Review of Economic Studies,1963,30(2):93-94.费希尔认为进行加总的条件非常严格，实际经济过程很难满足这些条件，因而总量生产函数的存在性及其同边际生产力理论的联系均非常可疑(13)Fisher,F.M.“The Existence of Aggregate Production Functions”.Econometrica,1969,37(4):553-577.，费希尔通过模拟实验进一步强调了C-D总量生产函数存在的问题，他使用明显违背加总条件的资本和劳动数据以C-D形式的生产函数进行模拟，反而得到了理想的拟合结果。(14)Fisher,F.M.“Aggregate Production Functions and the Explanation of Wages:A Simulation Experiment”.Review of Economics and Statistics,1971,53(4):305-325.但是，这些质疑并不能直接揭示C-D生产函数和收入恒等式的联系，比如费希尔就把拟合结果归因于不变的工资份额。(15)Fisher,F.M.“Aggregate Production Functions and the Explanation of Wages:A Simulation Experiment”.Review of Economics and Statistics,1971,53(4):305-325.谢克1974年的文章明确指出只需对国民收入等于工资加利润的恒等式进行变换，就可得到柯布-道格拉斯形式的总量生产函数(16)Shaikh,A.“Laws of Production and Laws of Algebra:The Humbug Production Function”.Review of Economics and Statistics,1974,56(1):115-120.，C-D总量生产函数同收入恒等式之间的联系才明确起来。谢克在文章中具体分析过程可以表示如下：

设Y为任意时期的总收入，w和r分别表示工资率和利润率，K和L分别表示资本投入和劳动投入。收入恒等式为：

Y=wL+rK

(1)

将式(1)两边对时间求导，并同时除以Y，可得：

(2)

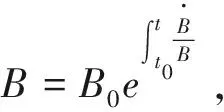
(3)

将式(2)两边同时从t0到t之间求定积分并将对数形式化为一般形式：

Y=BKsL1-s

(4)

式(4)与C-D生产函数形式Y=AKαL1-α非常相似。在柯布和道格拉斯的研究中，C-D生产函数中的资本和劳动的弹性系数α和1-α与利润、工资份额s和1-s非常接近。由于实际的经济事实很难满足加总条件，α和s数值上的相似并不是对边际生产力理论的证明。更有可能的是这两者在实际上是同一个变量，即α=s。经验研究中弹性系数与份额数值上的相似恰恰说明总量生产函数是源自收入恒等式的变形。谢克通过数值模拟对C-D总量生产函数的恒等式性质做了验证：他构建了一个产出劳动比Y/L和资本劳动比K/L的特殊数据集，其散点图正好是一个大写形式的“HUMBUG”(骗子)，利润份额使用索洛1957年文章中使用的数据，产出减掉通过利润份额计算得到的索洛余值后，剩余部分以C-D生产函数形式得到的拟合结果非常良好。谢克之后还引入了一个“完全拟合”程序，尽管这个程序完全曲解了潜在的生产关系和技术变革类型，却可将任何表现不佳的拟合生产函数转化为一个拟合结果非常好的函数。(17)Shaikh,A.“Nonlinear Dynamics and Pseudo-Production Functions”.Metroeconomica,2005,31(3),447-466.这一方面是对C-D生产函数的讽刺，另一方面也说明C-D总量生产函数的拟合效果和相关数据的数值特点无关，进一步证明C-D总量生产函数只是由一个无关生产的收入恒等式变换得到的。

从收入恒等式出发，可以发现由C-D总量生产函数得到的全要素生产率的实际含义。对式(3)两边从t0到t取定积分并将对数形式化为一般形式，可得

B=B0rsw1-s

(5)

将式(5)代入式(4)，由于s=α，可知A=B，继而可得B0=Y/rsw1-sKsL1-s。利用rK/Y=s与wL/Y=1-s，可得B0=s-s(1-s)s-1，最终可得到全要素生产率为

A=s-s(1-s)s-1rsw1-s

(6)

可见，全要素生产率实为利润与工资份额、利润率与工资率的函数，其直接反映的是要素价格和收入分配的结构，显然不能用来说明技术进步。之所以如此，根源仍在于从收入恒等式变换而来的C-D总量生产函数并不代表任何实际的生产过程。

(二)其他形式总量生产函数与收入恒等式的关系

除常用的C-D总量生产函数外，其他诸如CES与AK总量生产函数也可以通过收入恒等式构造得出，不同的总量生产函数不过是契合收入恒等式的不同方法。

1．CES总量生产函数、超越对数总量生产函数与收入恒等式的关系

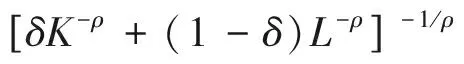
该式与对收入恒等式进行变换后的形式非常相近。说明这是比C-D生产函数适应性更好的CES生产函数，但并不代表真实生产的法则，只是找到了更能契合收入恒等式的方法。CES生产函数的假设比C-D生产函数更为放松，利润和工资份额都可以发生变化。费利普和马克比也就这一点做出说明。(19)Felipe,J.,and J.S.L.McCombie.The Aggregate Production Function and the Measurement of Technical Change:Not even Wrong.Cheltenham:Edward Elgar,2013.

超越对数生产函数比CES生产函数更容易估计，更为常用。一般多以对数形式表示：lnY=lnA+μlnK+νlnL+γ(lnK)(lnL)+ω(lnK)2+ε(lnL)2。费利普和马克比说明了只要超越对数函数符合边际生产力条件，就仍然完全来源于收入恒等式。事实上超越对数生产函数本身也是CES生产函数在ρ=0处的泰勒近似，如果CES不能摆脱恒等式，超越对数同样也不能。

2．AK总量生产函数与收入恒等式的关系

不仅上述外生增长模型具有这样的问题，以AK模型为代表的内生增长模型也可以通过收入恒等式得出。费利普和马克比分析了如何通过收入恒等式构造AK总量生产函数。(20)Felipe,J.,and J.S.L.McCombie.The Aggregate Production Function and the Measurement of Technical Change:Not even Wrong.Cheltenham:Edward Elgar,2013.

三、通过收入恒等式构造总量生产函数的一般方法

已有的研究揭示了几种总量生产函数与收入恒等式之间的联系，但仍缺乏一般性分析。我们在上述研究的基础上，通过一次齐次函数的欧拉公式将收入恒等式和总量生产函数联系起来，给出了通过收入恒等式构造总量生产函数的一般方法。相当于从本质上说明了总量生产函数为何会具有恒等式性质，以及全要素生产率的实际含义。

为了在总量生产函数的经验研究中得到良好的拟合结果，需要从收入恒等式出发，变换出一个形式上只与K和L有关的函数。构造总量生产函数关键在于利用一次齐次函数欧拉方程与收入恒等式形式上的相似性。如果总量生产函数Y=F(K,L)为一次齐次函数，由一次齐次函数的欧拉公式有：

Y=FKK+FLL

(7)

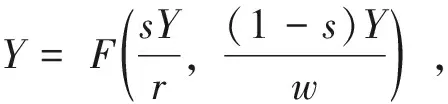
(8)

由于A是关于K和L的函数，所以这一条件很容易满足，但此时A就是一个内生变量，而不是主流学界所认为的一个外生的全要素生产率。在进行回归时，内生变量A的作用是让每一组投入产出数据均能符合收入恒等式，而非一个能够衡量生产的参数。正是这一性质，总量生产函数往往会得到良好的拟合结果，新古典经济学家认为这是总量生产函数符合实际情况的依据，甚至将包含内生变量A的AfK=r和AfL=w误认为边际生产力条件，但却忽视了其背后更重要的逻辑关系。

综上，只要f(K,L)满足一次齐次性质，函数Y=Af(K,L)就已完成构造总量生产函数的一般方法。而对AfK=r和AfL=w进一步变化，可以得到收入恒等式变换下总量生产函数中人为构造部分f(K,L)的参数实质，如下：

sf(K,L)=fKK

(9)

(1-s)f(K,L)=fLL

(10)

由式(9)、(10)可见，源自收入恒等式的总量生产函数其外生参数都将与要素的收入份额发生联系。比如对于C-D总量生产函数Y=AKαL1-α，直接由α=s。对于其他形式的f(K,L)，可以通过式(9)与式(10)得到这些参数与s、K、L的关系。例如，把CES总量生产函数中的[δK-ρ+(1-δ)L-ρ]-1/ρ替代f(K,L)代入式(9)和式(10)，可以得到δ=sKρ/[sKρ+(1-s)Lρ]与1-δ=(1-s)Lρ/[sKρ+(1-s)Lρ]。可以看到，当f(K,L)包含两种以上的参数时，这些参数的外生给定也会使得利润和工资份额s、1-s随着K、L的变化而变化。因此，总量生产函数的参数其实都是人为设定的，任何参数都可以通过收入恒等式获得。

在不改变函数形式的前提下，将K、L替换为K和L的函数甚至其他变量，都不会改变基于收入恒等式构造总量生产函数的实质。例如，引入人力资本的总量生产函数，也不能突破构造总量生产函数的范式。尽管费利普和马克比已经说明引入人力资本几乎不影响产量和TFP增长率(22)Felipe,J.,and J.S.L.McCombie.The Aggregate Production Function and the Measurement of Technical Change:Not even Wrong.Cheltenham:Edward Elgar,2013.，但是即便有所影响，人力资本模型中联合人力资本H与劳动L构造效率劳动L*=HL的方法，也无非是以L*代替总量生产函数中的L，没有对总量生产函数造成实质性的改变。加入资本增益型技术进步和劳动增益型技术进步的总量生产函数Y=Af(AKK,ALL)也不例外，无需对式(9)和式(10)做调整，就能以此构造总量生产函数。

综上，既然f(K,L)可以通过以上方式构造出来，那么从式(8)也可以清楚地看到全要素生产率A根本无关生产，而只取决于f(K,L)的设定及其和收入的比值。进一步，AfK=r与AfL=w是通过收入恒等式构造总量生产函数的关键条件，同时也会使得f(K,L)规模报酬不变。由rK/Y=s与wL/Y=1-s，可得K=sY/r、L=(1-s)Y/w。将其代入Y=Af(K，L)，得到Y=Af[sY/r,(1-s)Y/w]，由于函数f(K,L)为规模报酬不变，等式右边可将Y提出，最终可得到全要素生产率为：

(11)

相比于式(6)，式(11)是一个全要素生产率的一般表达式。这意味着不管什么形式的总量生产函数，由此得到的全要素生产率都只是一个关于利润和工资份额、利润率、工资率的分配函数。至此，可以明确所有和总量生产函数有关的全要素生产率都是可疑的。由于当前测算全要素生产率的方法种类庞杂，并且在估计过程中仍有需要探究的细节，故下文我们将进一步具体分析。

四、收入恒等式视角下的全要素生产率测算方法探究

测算全要素生产率的很多方法并非简单地基于总量生产函数，这在表面上削弱了收入恒等式问题的威胁。例如马哈德文在其讨论全要素生产率的文章中就已提到收入恒等式问题，但他认为通过多种不同方法测算全要素生产率总能得到一定的规律，没必要执着于全要素生产率的实际含义(23)Mahadevan,R.“To Measure or not to Measure TFP Growth?”.Oxford Development Studies,2003,31:365-378.，这类观点认为总有一种测算全要素生产率的方法可以避免总量生产函数所遭遇的问题。然而，只要仍使用货币形式的产出数据，无论以何种方式将投入和产出联系起来，都很难撇清全要素生产率和收入恒等式的关系。参照马哈德文关于全要素生产率测算方法的归类，我们将针对参数方法与非参数方法进行讨论。

(一)参数方法

参数方法要求明确函数形式，在测算的过程中总量生产函数是不可或缺的。总量生产函数的恒等式性质使得参数方法所计算的全要素生产率并不符合其测度生产与技术的目的。此处我们重点讨论索洛残差法和收入恒等式的联系。

索洛残差法首先估算总量生产函数后得到要素产出弹性，再用产出增长率减去各要素以其产出弹性加权后的增长率，得到全要素生产率的增长率。具体如下：

(12)

其中，α和β为资本产出弹性和劳动产出弹性，一般通过回归方程估计得到。通常回归方程假定规模报酬不变，即β=1-α，并使用Y/L和K/L进行回归。考虑到全要素生产率A的变化，回归方程中往往加入时间趋势项。以C-D总量生产函数为例，估计方程为：

ln(Yt/Lt)=a+φt+αln(Kt/Lt)+εt

(13)

当估计得到α=s，β=1-s时，此时全要素生产率的增长率实际为：

(14)

这样，以索洛残差法测算的全要素生产率增长率为利润率增长率与工资率增长率的加权和。一些研究假设市场完全竞争把要素份额作为要素产出弹性直接计算索洛余值，近乎直接使用式(14)得到源于恒等式的分配函数。之所以得到α=s，关键在于对数回归方程中的索洛残差是否等于式(14)中工资率与利润率的对数加权和。(24)Felipe,J.,and C.Holz.“Why do Aggregate Production Functions Work? Fisher’s Simulations,Shaikh’s Identity,and Some New Results”.International Review of Applied Economics,2001,15(3):261-285.当估计得到α≠s时，根据式(12)计算的全要素生产率增长率又代表什么呢？坦普尔认为，这种情况下总量生产函数并不是收入恒等式的变形，甚至回归方程中用于近似索洛残差项如果选取得当，可以反映真实的生产情况。(25)Temple,J.R.W.“Aggregate Production Functions,Growth Economics,and the Part-time Tyranny of the Identity:A Reply to Felipe and McCombie”.International Review of Applied Economics,2010,24(6):685-692.然而，无论在回归方程中如何预设索洛残差，方程中都不存在任何实际生产的信息。鉴于这一点，我们认为，这种情况也没有完全脱离收入恒等式。实际上，该情况源于以α与(1-α)为比例重新分割收入而得到的新的恒等式。假设有w′=(1-α)Y/L、r′=αY/K，将α与(1-α)代入式(12)，计算得到全要素生产率A′，根据收入恒等式变换的原理，可以得到A′的增长率如下：

(15)

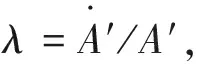
(二)非参数方法

非参数方法测算TFP确实可以避免预先设定总量生产函数，但仍很难摆脱恒等式性质的影响。当产出为货币数据，产出和要素之间最直接的关联就是要素价格，并由此建立收入恒等式，只要全要素生产率的概念指向有形要素之外的生产贡献，就会和要素价格产生联系，因此全要素生产率必然是一个关于要素价格的分配关系的函数。

(16)

其中，m=1,…,M、n=1,…,N。在具体的TFP计算中，令t时期i单元的产出为Yit，投入要素为资本Kit、劳动Lit，代入式(16)后用单纯形法进行计算。可知，最优解时θi不为0，因此，包括θi最优基变量共有三个，设另外两个最优基变量为zτt和zυt，对应单元的产出、资本与劳动分别为Yτt、Kτt、Lτt和Yυt、Kυt、Lυt，DEA问题则转变为如下方程组的求解：

(17)

现在以收入恒等式的视角进行考察：我们仍以s、1-s、r、w代表利润份额、工资份额、利润率、工资率，下角标第一个字母代表单元，第二个代表时间。设t时期单元τ和单元υ的利润份额、工资份额、利润率和工资率分别为sτt、1-sτt、rτt、wτt和sυt、1-sυt、rυt、wυt。由收入恒等式可知有Kit=sitYit/rit、Lit=(1-sit)Yit/wit、Kτt=sτtYτt/rτt、Lτt=(1-sτt)Yτt/wτt、Kυt=sυtYυt/rυt、Lυt=(1-sυt)Yυt/wυt，将其代入式(17)，产出Yit、Yτt、Yυt最终会被消掉，可得

(18)

可见，通过DEA计算出的距离函数的倒数θi只与要素收入份额、利润率和工资率有关。因此由基于距离函数的曼氏生产力指数得到的TFP增长率，也只与要素收入份额、利润率、工资率有关，实质上仍然是一个与分配关系有关的函数。系统中某个单元的工资利润分配发生变化，该单元的TFP就有可能受到影响。DEA方法之所以无法摆脱恒等式性质的影响，仍然在于货币统计的产出中很难触及生产与技术的实质。非参数方法中也有不使用货币产出数据的方法，比如迪氏指数法(Divisia index)中的汤氏指数( Törnqvist index)也常被用于测算全要素生产率。这类方法虽然可以提供一种产品加总指数来代替货币统计的产出，却并不像参数方法那样可以用拟合效果作为参考，因而仍然需要一个评价标准。如果按照新古典经济学以最优化来简化问题的逻辑，这些指数一旦和最优化联系起来，并且在难以兼顾要素价格变化的情况下，就容易和收入恒等式发生联系。比如迪韦特就证明了汤氏物量指数等同于满足约束下最优化条件且规模报酬不变的超越对数函数。(27)Diewert,E.W.“Exact and Superlative Index Numbers”.Journal of Econometrics,1976,4:115-146.而实际上由收入恒等式变换来的超越对数总量生产函数完全符合它的函数要求。汤氏物量指数因为近似于最优化超越对数生产函数得到不错的评价，但这恰恰是它失去生产含义的原因。测算全要素生产率，不论参数方法还是非参数方法，均不能摆脱总量生产函数的恒等式性质。

五、经验研究：全要素生产率的实际含义

本文的第三部分已经讨论了全要素生产率的测算方法与收入恒等式之间的关系，虽然这些方法与收入恒等式的联系都可以在理论上充分说明，但是参数方法的估计结果仍需要经验研究的支持。限于篇幅，我们这里只检验索洛残差法计算的TFP增长率与收入恒等式的联系。我们的经验研究与前人研究的最大区别在于揭示了实际估计中得到的全要素生产率与利润率、工资率和要素收入份额之间的关系，揭示了全要素生产率的实际含义。尤其是当估计得到的弹性值不等于要素收入份额值的情况下，不同于谢克等人的模拟数据研究，我们用国内宏观经济实际数据来检验全要素生产率是否具有生产含义。

(一)数据来源与处理

为了计算我国的全要素生产率，我们需要实际产出、资本存量、劳动投入的数据，这些数据均可从我国官方统计资料中获得，选取的时间跨度为1993—2016年。选择这一时间段的原因是省际收入的可靠数据仅从1993年起始。

(1)实际产出Y与劳动投入L。实际产出用GDP表示，GDP数据来自2017年《中国统计年鉴》，利用1978年按当年价格核算的GDP和以1978年不变价计算的GDP指数，可以计算出以1978年不变价格计算的GDP；劳动投入用就业人口表示，数据也来自2017年《中国统计年鉴》。

(2)资本存量K。资本存量我们采用永续存盘法进行计算，即Kt=(It/Pt)+(1-δ)Kt-1，其中It是以当年价格计算的第t年投资额，Pt是第t年价格水平，δ为折旧率。为了与GDP数据保持一致，资本存量也需换算为以1978年价格计算的数据。我们采用张军和章元以1990年不变价估计的结果(28)张军、章元：《对中国资本存量K的再估计》，载《经济研究》，2003(7)。，再使用固定资产价格指数，换算得到1978年不变价计算的K0为13 243.78亿元。我们采用固定资本形成总额作为投资额It的指标。在《中国国内生产总值核算历史资料(1952—2004年)》中可以找到以1978年价格计算的1993—2004年的固定资本形成总额指数，结合该资料中记录的1978年按当年价格计价的固定资本形成总额，可以得到以1978年价格计算的1993—2004年固定资本形成总额数据。在2017年《中国统计年鉴》中可以找到以1990年价格计算的2004—2016年的固定资产投资价格指数，根据《中国国内生产总值核算历史资料(1952—2004年)》的数据换算出以1978年价格计算的2004—2016年的固定资产投资价格指数，结合《中国统计年鉴》中以当年价格计算的固定资本形成总额，计算得到以1978年价格计算的2004—2016年的固定资产价格指数。关于折旧率δ，我们选择较为常见的5%，最终计算得到1993—2016年的国内资本存量数据。

(3)利润份额s与工资份额1-s。我们首先获得劳动收入份额的数据，然后根据w=(1-s)Y/L和r=sY/K就可计算出利润率与工资率。本文采用省际收入法的数据加总得到1993—2004年劳动收入份额(省际收入的可靠数据仅从1993年起始)，数据来源为《中国国内生产总值核算历史资料(1952—2004年)》，2005—2007年、2009—2012年以及2014—2016年的劳动收入份额则来自相应年份《中国统计年鉴》收入法统计GDP里的劳动报酬数据。其中，2004年出现了统计口径的变化：个体经营户的收入由劳动者报酬改为营业盈余，国有和集体农场的营业盈余划入劳动者报酬。同时，有学者推测，从2009年开始统计口径恢复到2004年之前(29)张车伟：《中国劳动报酬份额变动与总体工资水平估算及分析》，载《经济学动态》，2012(9)。，所以必须对2004—2007年的劳动收入份额进行调整。我们参考肖文和周明海的调整方法(30)肖文、周明海：《劳动收入份额变动的结构因素——收入法GDP和资金流量表的比较分析》，载《当代经济科学》，2010(3)。,在相应年份的《中国劳动统计年鉴》中找到城镇私营与个体就业人员的数据，继而得到非个体就业人数，再用就业人数与非个体就业人数做比并乘上劳动报酬，得到调整后的劳动报酬和劳动收入份额。由于《中国统计年鉴》并未记录2008年和2013年的收入法GDP的统计数据，我们在调整份额之后，2008年的劳动份额取2007年和2009年数据的均值，2013年的劳动份额取2012年和2014年数据的均值。

(二)检验过程与结果

经验研究的重点分为三步：第一步检验以初始生产函数形式进行回归得到的TFP增长率的实际含义；第二步检验在回归方程中加入时间趋势后所得到的TFP增长率的实际含义；第三步计算源于实际收入恒等式的TFP增长率。然后总结出TFP增长率计算的实质。

我们采用C-D总量生产函数的形式。为了和收入恒等式充分联系起来，将估计得到资本产出弹性与资本收入份额进行比对。我们计算的1993—2016年间中国的资本收入份额在0.5附近波动。分别用三次不同的回归方程进行回归后的结果如表1：

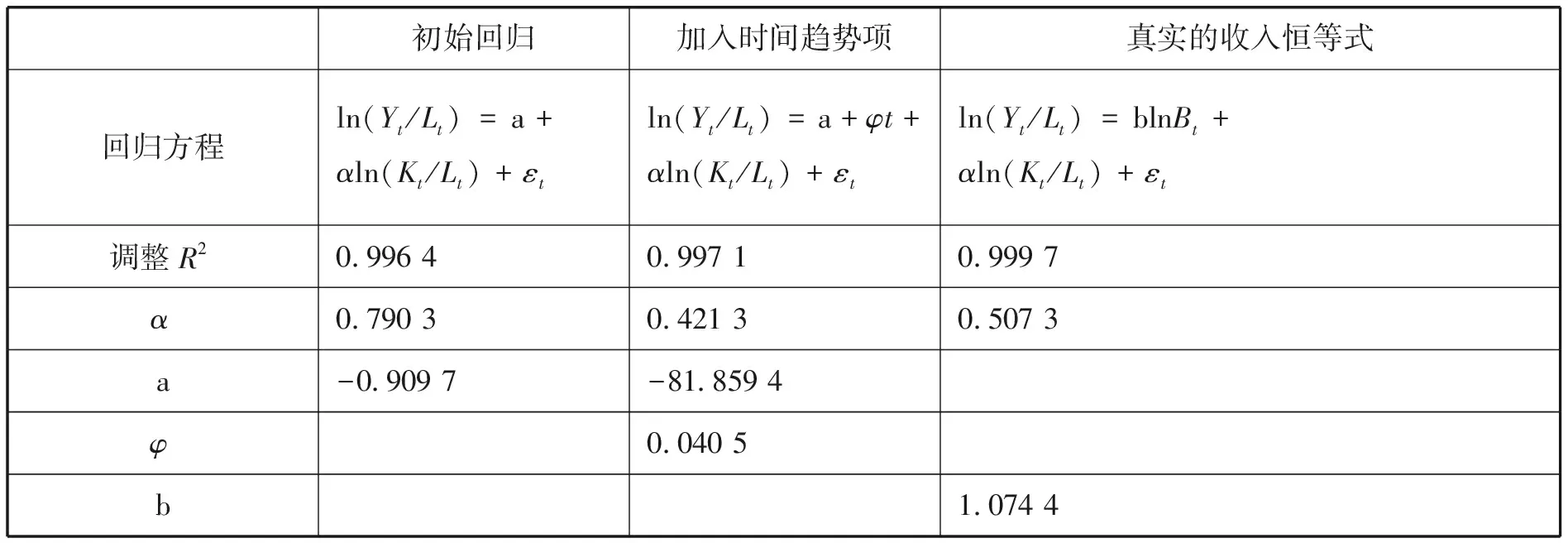
表1 回归方程及结果

首先，我们根据C-D生产函数的形式，利用国内产出、资本与劳动数据，直接用Yt/Lt对Kt/Lt进行对数线性回归，估计得到的资本产出弹性为0.790 3；第二步我们用Yt/Lt对Kt/Lt和年份t进行回归，估计得到的资本产出弹性为0.421 3，两者均与0.5左右的资本收入份额有较大差异。但根据前述分析，参数估计的结果只是得到了一种分割收入的方式。分别以0.790 3∶0.209 7和0.421 3∶0.578 7为比例分割总收入，将前一部分视为资本收入，后一部分视为劳动收入，得到新的利润率、工资率，分别记为r′、w′和r″、w″，通过式(14)计算出增长率加权和，然后利用式(12)计算索罗残差得到TFP增长率。增长率加权和与TFP增长率趋势对比如图1所示：

图1 TFP增长率与w′、r′和w″、r″增长率加权和变化趋势对比

第一步回归得到的资本产出弹性值，并不是因为它符合实际生产情况，而是由于回归方程的形式相当于假定索洛残差项不随时间t变化。换言之，回归过程其实只是找到一个使w′、r′的对数加权和[slnr′+(1-s)lnw′]不随时间t变化的利润份额s，这里的利润份额s不是真实的利润份额，而是能够使w′、r′的对数加权和不随时间t变化的分割总收入的一种方式。(31)对式(6)取对数可得lnA=lns-s(1-s)(s-1)+slnr+(1-s)lnw，s是需要回归得到的利润份额，第一项lns-s(1-s)(s-1)不随时间变化而改变，只需工资率w和利润率r的对数加权和slnr+(1-s)lnw保持不变即可。引入时间趋势项的回归方程能够得到的资本产出弹性值，也是通过回归过程找到了一个使得w″、r″的对数加权和与时间t呈线性关系的分割比例。我们计算了w′、r′和w″、r″对数加权和的时间趋势，结果如图2：

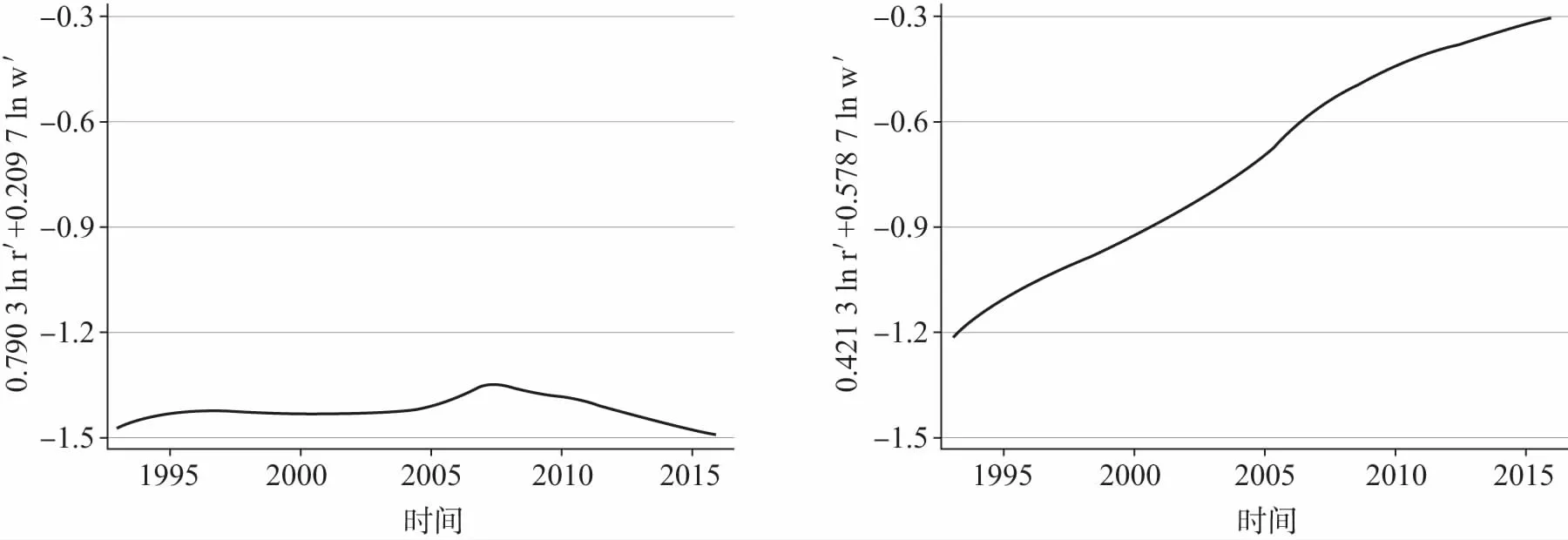
图2 w′、r′和w″、r″对数加权和的时间趋势对比

从图2可以看出，w′、r′的对数加权和随时间变化很小，其结果符合对初始回归方程的分析，通过回归方程确实找到了一个使得w′、r′的对数加权和大体不变的分割收入的比例。w″、r″的对数加权和确有接近于线性的时间趋势，加入时间趋势项的回归方式也的确找到了一个使得w″、r″的对数加权和与时间t呈线性关系的分割收入的比例。由此可见，无论是否加入时间趋势项，通过索洛残差法得到全要素生产率的方法，只是找到一种分割收入的比例，使其满足回归方程，并不能代表真实的生产过程。

前面的两种回归只是提供了两种分割收入的方式，如果想得到符合实际收入恒等式的结果，需要在回归方程中以工资率利润率的对数加权和来表示索洛残差项。谢克等人契合收入恒等式的经验研究也相当于采用了这种方法。(32)Shaikh,A.“Laws of Production and Laws of Algebra:The Humbug Production Function”.Review of Economics and Statistics,1974,56(1):115-120；Felipe,J.,and C.Holz.“Why do Aggregate Production Functions Work? Fisher’s Simulations,Shaikh’s Identity,and Some New Results”.International Review of Applied Economics,2001,15(3):261-285.我们使用实际的利润和工资份额、利润率、工资率，计算出式(6)所表示的分配函数s-s(1-s)s-1rsw1-s，此处记为Bt。在初始的对数回归中加入lnBt，回归结果见表1。

这样估计得到的资本产出弹性0.507 3与实际的资本收入份额比较接近。不同于前面使用估计的参数，此处我们使用实际的劳动收入份额和资本收入份额，根据式(14)计算出实际的工资率与利润率w、r的增长率加权和。继而使用估计得到的结果α=0.507 3、β=0.492 7，计算得到TFP增长率。可得到图3：

图3 TFP增长率与w、r增长率加权和变化趋势对比

尽管我们计算w、r的增长率加权和时使用了每年都有所变化的利润和工资份额，但从图3可知，w、r的增长率加权和仍然和TFP保持了比较一致的趋势。所以，在契合收入恒等式的情况下计算的TFP增长率是实际分配关系的函数。与前面一样，估计得到的参数仍然可以视为分割收入的比例，但这次估计是为了使分割收入而得到的对数加权和符合实际的工资率与利润率的对数加权和lnBt。因此，估计得到的资本产出弹性恰好等于资本收入份额，并不代表证明了边际生产力条件，而是因为回归方程中加入的余项恰好符合工资率与利润率以利润和工资份额为权重的对数加权和。

如果lnBt数据呈不变或线性变化趋势，第一步与第二步回归方程均有可能得到符合收入恒等式的结果。谢克指出工资率与利润率的对数加权和可以近似于时间的一次函数，这说明在第二步回归方程中加入趋势项就能得到近似收入恒等式的结果。我们可以看到图1(右)与图3中TFP增长率的变化趋势非常相似，在一定程度上也验证了这一点。

从以上三步回归方程的结果可以看到，估计出何种资本产出弹性，计算出怎样的全要素生产率，取决于我们在回归方程中用什么来代表索洛残差。这种方法的实质就是循环论证。我们在回归方程中关于索洛残差的任何假定实际上都没有事实根据，但这些假定却已经决定了全要素生产率的计算结果。不同的测算方法和资本数据都会改变回归方程的预设，所计算得到的结果也只是符合预设的结果，并没有哪种方法能涉及实际的生产过程。虽然最终的估计结果未必贴合实际的收入恒等式，但通过收入恒等式的变换可以令我们清楚认识到索洛残差法的实质就是分割收入。无论我们估计得到的要素产出弹性是否等于要素的收入份额，以索洛残差法计算的全要素生产率都只是一个分割收入得到的分配关系的函数。

六、结论

我们在谢克、费利普等人所做的收入恒等式问题研究的基础上，给出了通过收入恒等式构造总量生产函数的一般方法；详尽地分析了全要素生产率与收入恒等式的关系，阐明了全要素生产率测算的实质；说明了以索洛残差法测算的全要素生产率是一种由分割收入而得到的分配关系的函数。作为分配关系函数的全要素生产率并非完全不能表示技术进步或效率改进，但前提是必须厘清该指标中表示生产和分配的成分。然而在总量问题仍需依托现有国民经济核算体系的情况下，由于工资率、利润率与资本劳动的复杂关系，很难将生产与分配彻底隔离开来。基于总量生产函数的恒等式性质测算的全要素生产率无法代表实际生产过程中的技术或效率，用其解释技术进步时一定要更为审慎。根植在经济学研究中的工具主义方法论可以让研究者放松假设，但却不能无视测算方法中所存在的逻辑矛盾。从总量均衡入手分析宏观问题难免会产生这一问题，因为总量均衡分析仅仅停留在事物的表面，没有对微观产业层面进行具体分析，无法探究总量变化的机制。为规避这一问题，在宏观经济学的研究中，应避免仅从宏观统计角度分析问题，尽量寻找其背后的逻辑与机制，比如可以尝试从微观企业层面测度技术创新，尽管从微观入手不如使用宏观数据简洁，但更加具体和贴近事实，且不会产生恒等式问题。或从收入分配角度出发，如谢克等人通过工资与利润份额的变动分析经济增长及失业、通货膨胀等问题。(33)Shaikh,A.Capitalism,Competition,Conflict,Crises.Oxford:Oxford University Press,2016.将宏观统计数据与机制分析相结合，就不会赋予宏观经济变量并不具备的因果意义。