问题教学,从“备教”走向“备学”
2019-11-23宁俊玲
宁俊玲

“问题教学”是由某本原性数学问题所引发的探究、建模,直至达成问题解决的教学活动,着力培养学生的思维方式,帮助学生形成应对未知挑战的能力。
一、从随意的提问到本原性问题凝练——真问题
本原性数学问题的凝练,要考虑数学作为一种活动,其内在的联系、思想方法等本质特征;更要考虑对学生而言,什么是某个数学问题最为本质的要素。本原性数学问题的凝练重在关注问题的“质”,即在数学教学中把某个数学问题的“根源”或“基本构成”作为思考的第一问题。根据苏联心理学家维果茨基的“最近发展区”理论,开课后的第一个5分钟是激活学生大脑的最佳时段,问题引发能迅速而巧妙地缩短师生间以及学生与教材间的距离。一节课的本原性问题凝练,可以从知识体系、思想方法与核心概念入手。下面以“分数的基本性质”的问题引发为例进行说明。
师:你能说出下面各题中横线上应该填哪些数字吗?说说你这样填的理由。
1÷2=(1×4)÷(2× ) 2÷4=(2×10)÷(4× )
4÷8=(4÷ )÷(8÷ )
生1:第1小题被除数1乘了4,除数2也要乘4。
生2:这是根据商不变的性质填空的,被除数和除数都乘4,左右两边才相等……
师:你能说说什么是商不变的性质吗?
生3:被除数和除数同时乘或除以一个非0的数,商不变。
生4:被除数和除数同时乘或除以相同的数(0除外),商不变。
师:除法有商不变的性质,而分数和除法是有关系的,分数是不是也有类似的规律呢?今天就来学习分数的基本性质(板书课题)。
教师找准新旧知识的连接点,引发学生思考:除法有商不变的性质,而分数和除法是有关系的,分数是不是也有类似的规律。这就指向了本课要研究的问题,为学生搭建了探究的台阶。再如五年级下册“异分母分数加减法”的问题引发。
师:9.8-7 = 9.1,这个计算对吗?
生1:计算不对,正确答案应该是2.8。
生2:因为7在个位上,表示7个一,不能用9.8的十分位上的数字8去减,应该用个位上的9去减。
师:为什么?
生2:相同数位上的数字才能相加减。因为相同数位上的数单位相同,单位相同的数才能直接相加減。
师:(出示日常生活垃圾分类表)观察图表(见图1),食品残渣和纸张一共占生活垃圾的几分之几?
生3:这两个分数的分母相同,也就是分数单位相同,分母不变,分子相加。
师:纸张和废金属一共占生活垃圾的几分之几?
生4:+。
师:能像刚才那道题一样直接分子相加吗?
生4:不能,因为分母不同。
师:分母不同的分数称为异分母分数,异分母的分数该怎样相加减呢?(留时间给学生思考)这节课就来探究分母不同的分数加减法的计算方法。(板书课题:异分母分数加、减法)
单位相同的数相加减是学习异分母分数加减法的核心概念,抓住了单位相同的数相加减也就抓住了异分母分数相加减的算理,也就抓住了本节课的核心。从辨析小数减法、同分母分数加减法中,体会进行相同单位的数量的个数的增减,再体会到异分母分数不能直接相加减的原因是单位不同,进而理解异分母分数的加减法必须先通分的算理。这样就使学生一下子触及了教学内容的实质。
“学起于思,思源于疑”。学生如果有疑问,就会感到困惑。只有激发学生的认知冲突,使学生处于“认知失衡”的状态,才能更好地激发学生的探究欲望。数学知识系统性强,旧知识是新知识的基础,新知又是旧知的发展和延伸。把握住学生认知起点在哪里、困惑在哪里,让学生自然而然地产生学习需求,感到新知不新,难点不难,教师才能教得顺畅、学生才能学得轻松,课堂学习真正成为学生的自主学习行为。
二、从抄教案到研制学习单——真备课
要实现学习真正发生,变传授、灌输为自主、合作、探究学习,不是仅凭现成的教材或者教学参考书就能够做到的。基于深度学习实验的教学课堂,不要大而广,要精而深。唯一的办法就是整合、取舍、凝练。整合、取舍就是提出核心问题,把核心问题分解成问题串,对教材内容进行整合。这就需要教师打破以往仅仅抄写教案,使课堂与教案脱节的备课模式。
基于深度学习的数学“问题教学”,以“学习单”作为备课载体,翻转了传统的备课思维。学习单的设置以本原性问题驱动,以纲领级的问题进行引领,抓重点与主干,忽略细枝末节。探究清单是学习单的核心,围绕本原性问题设置的问题串之间紧密联系,呈现进阶或并列关系。问题由简到繁、由易到难,引领学生探究知识的方向。下面以进阶式问题探究和并列式问题探究两种探究方式的学习单为例进行说明。
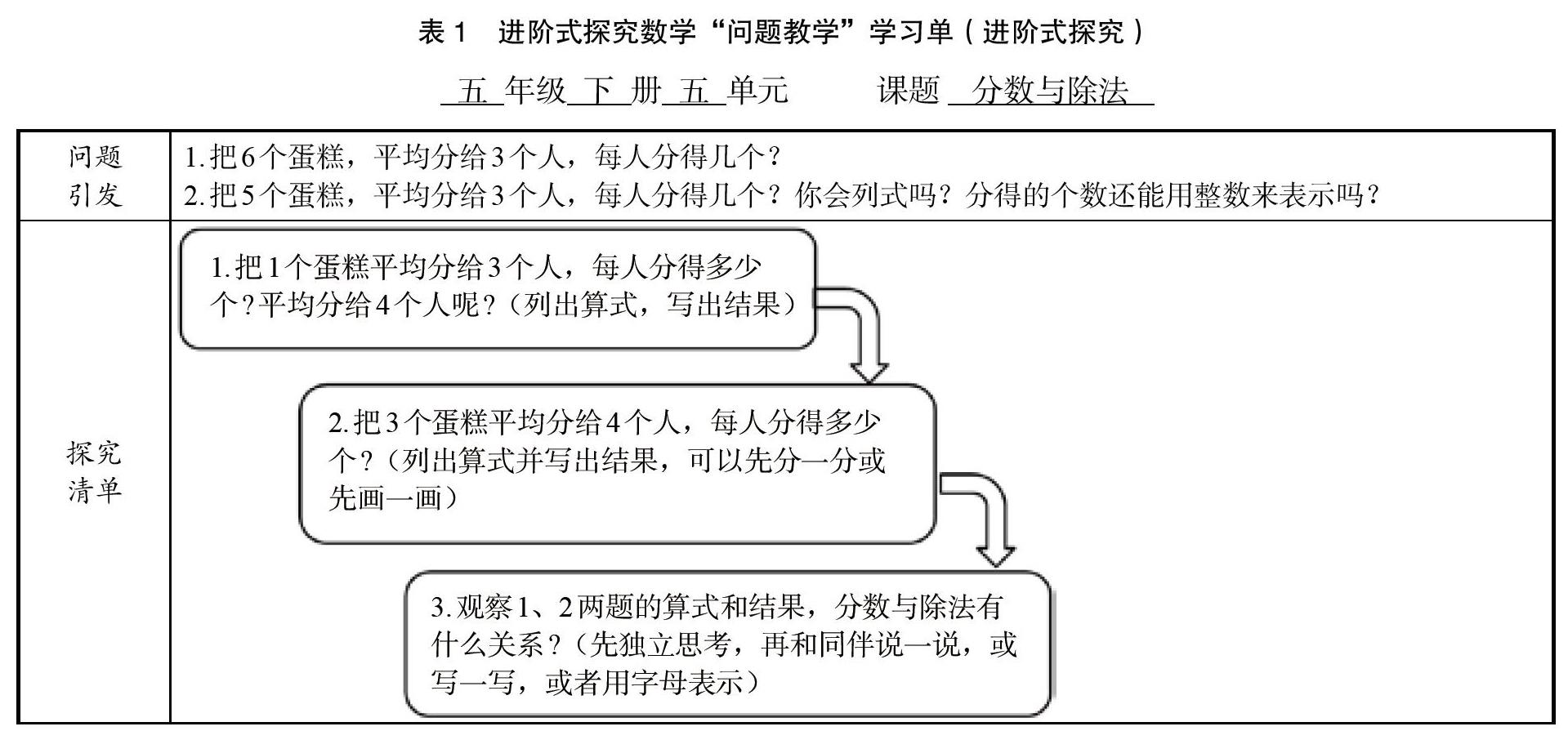
进阶式问题探究课的结构为“问题引发—进阶式探究—建立模型—问题解决”(见表1)。
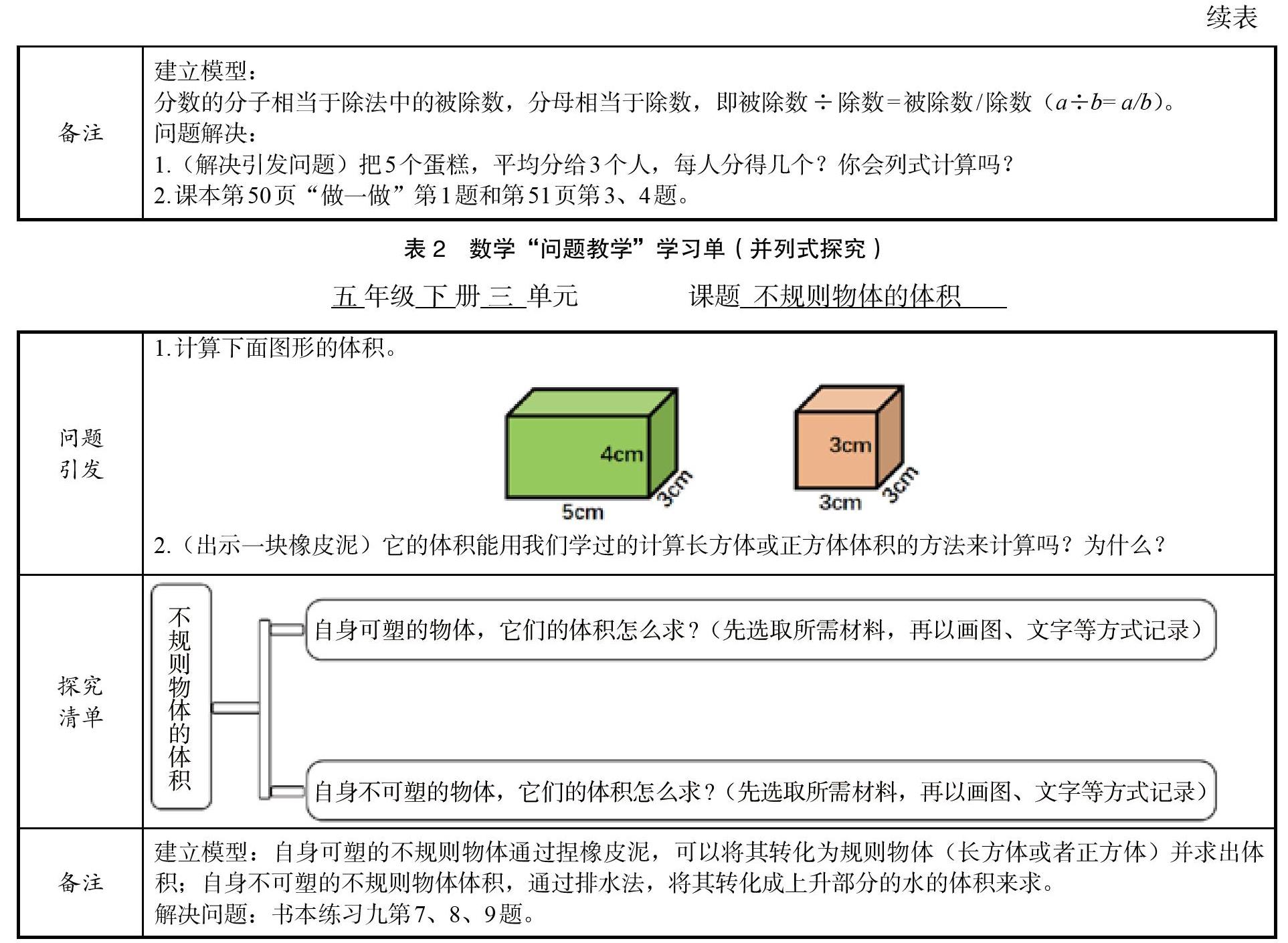
并列式问题探究课的结构为“问题引发—并列式探究—建立模型—问题解决”。进阶式问题探究课和并列式问题探究课两种课型的区别在于第二环节—探究清单(见表2)。
问题探究(问题清单)的问题设置要求关注问题的“质”,即问题触及数学的本质,指向本节课的核心知识点。这个本质,可以指知识、技能,也可以是基本思想与基本活动经验,有一定的开放性和引导性,能够为学生提供独立思考与主动探究的空间。问题相对较综合,能覆盖不同层次的学生,关注不同学生的差异发展;问题串少而精,一节课一般围绕2~3个问题进行研究。如《分数与除法》图示为进阶,指导学生由问题1~3顺次研究,学生的自主探究以此为抓手,拾级而上,有的放矢。探究清单中的问题串用图示进阶或并列,对学生探究作具体、简洁的操作提示,让学生知道如何做才能完成学习任务,让学习单真正成为学生自主探究学习的“脚手架”。
这种大板块的教学设计,环节清晰,问题聚焦,让有价值的问题串在数学教学中充分发挥效用,真正让学生“在做中积累数学经验”,张扬思维个性化;实现数学教学“从冗繁走向凝练,从紧张走向舒缓, 从肤浅走向深邃,从杂乱走向清晰”;帮助学生形成相对稳定的与数学有关的见解或者思路,真正培养解决复杂问题的能力。这种深度学习能力,能在学生的学习、生活和职业生涯中成为其发展的重要支撑点。
(作者单位:广东省东莞松山湖中心小学)
责任编辑:孙昕
heartedu_sx@163.com
