含三维内裂纹试件单轴压缩裂纹扩展机理及数值模拟

杨海平

(浙江同济科技职业学院 建筑工程系， 杭州 311231)

缺陷与裂纹作为岩体的固有属性，一直以来是学者们的研究热点[1-2]．对于诸如水利，岩土，采矿等领域，岩体的裂纹和缺陷在复杂应力条件下的扩展会导致岩体结构的失稳破坏[3-4]，因此研究岩体的裂纹扩展规律，对其机理的正确认识对防止岩体结构破坏有及其重要的作用．

对于含裂纹岩体在各种应力作用下的裂纹扩展规律及破坏过程，国内外许多学者进行了大量的研究，试验方面：宫凤强[5]利用花岗岩矩形隧洞试件在单轴压缩下的裂纹扩展破坏过程进行了试验研究，得到了不同加载方式下的破坏模式；张盛[6]对不同预制裂缝长度下的NSCB试件进行了三点弯曲断裂试验，得到了不同预制裂纹长度下的试件的断裂韧度；徐辰宇[7]对CO2增强型采热(CO2-EGS)工程中CO2作用下岩石的水压破裂进行了试验研究，得到了CO2压裂的裂纹扩展形态．数值模拟方面：李竟艳[8]利用Abaqus软件对单轴拉伸下的岩石材料的裂纹扩展进行了数值模拟；李宏[9]利用离散元软件PFC对含非贯通裂隙岩体的裂纹扩展进行了数值；王海军等[10]利用三维裂纹分析软件Franc3d对含裂纹孔洞试件在单轴压缩下的裂纹尖端应力强度因子进行了数值模拟分析．但是，以上研究仅仅针对于二维穿透型裂纹或者是三维表面裂纹进行研究分析，事实上，裂纹以三维内裂纹形态存在于岩体中，片面的将三维内裂纹简化为二维裂纹会丢失掉许多必要的信息[11]，对于三维内裂纹的研究相对较少，且多集中于对三维裂纹的表象的研究，如付金伟[12-14]对新型树脂材料含三维内裂纹树脂进行了试验研究，得到了裂纹扩展规律及破坏形态，同时，对于三维内裂纹裂纹扩展及应力强度因子计算的数值模拟也是一个难点[15]．

本文对三维椭内圆裂纹的始裂状态进行了解析分析，并基于M积分及最大周向拉应变准则对三维椭圆内裂纹的裂纹前缘的应力强度因子及裂纹扩展规律进行了数值模拟，研究结果为正确认识三维内裂纹的扩展机理及三维内裂纹的扩展过程的数值模拟提供了方向．

1 椭圆内裂纹始裂状态的解析分析

1.1 裂纹前缘扭转角的解析表达

对于处于压剪状态下的椭圆裂纹，裂纹面承受压力与剪力，根据李世愚[16]等的研究，此时一型应力强度因子KⅠ为0，而KⅡ，KⅢ则不为0．裂纹面上的正应力与剪应力可以表示为如下形式：

(1)

其中，σc是裂纹面的正应力，而τc为裂纹面的剪应力，σ为试件所受到的外加应力，f为裂纹面间的摩擦系数，α为裂纹面与加载方向的夹角．

预制椭圆裂纹前缘某一点P在局部坐标系下，三维应力分量以极坐标形式可以表示为：

(2)

式中，KⅡ，KⅢ为二型，三型应力强度因子．

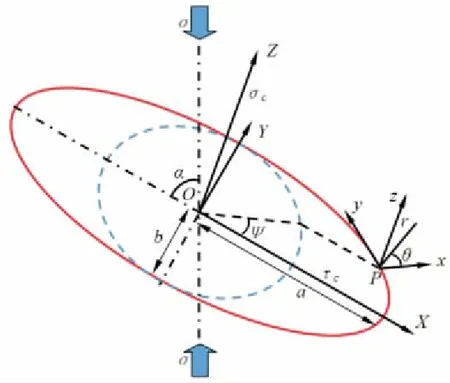
图1 裂纹面标识

对于压剪下的椭圆裂纹扩展形式主要有弯折型与扭转型，如图2所示．当发生二型裂纹扩展时，裂纹面沿原裂纹面扩展一个θ的转角，而当发生三型裂纹扩展时，裂纹扩展面则沿着原裂纹面扭转一个Φ的转角．

图2 不同裂纹扩展形式

基于此，可以得到由起裂面空间的θ与Φ共同决定的法向应力σN表达式：

σN=σxx·sin2(θ)·cos2(θ)+σyy·sin2(φ)+

σzz·cos2(θ)·cos2(φ)-2τxysin(θ)·

sin(φ)·cos(φ)-2τyzcos(θ)·sin(φ)·cos(φ)-

2τxzsin(θ)·sin(φ)·cos2(φ)

(3)

其中，应力强度因子的解析解可由式(4)给出[17-18]：

(4)

其中，Ψ为椭圆的极角，η′=b/a，η2=1-η′2，B=(η2-ν)·E(η)+η′2·E′(η)，E(η)，E′(η)分别为第一类与第二类完全椭圆积分．

定义应力集中系数δ=σN/σ，对二元函数(3)求极值：

(5)

便可求得椭圆裂纹前缘的始裂状态下的裂纹前缘的转角θ和扭角Φ随着椭圆的极角Ψ的变化，通过数值计算便可计算出椭圆裂纹前缘的每一点的裂纹扩展角度．

1.2 裂纹前缘的实例计算

对文献[13]中的树脂材料进行计算，裂纹参数如下：椭圆裂纹的长半轴a=10 mm，短半轴长b=7.5 mm，裂纹间的摩擦系数f取为0.1，泊松比ν为0.2，角度α=45°，计算半径r参照文献[18]的取值取为0.01 mm，至此，可以由式(5)得出转角θ和扭角Φ随着椭圆的极角Ψ的变化，利用数学计算软件Mathematica对式(5)进行数值计算，转角θ，扭角Ψ随裂纹前缘的变化曲线如图3所示．

图3 裂纹前缘扭角与转角的关系

由图3可得：裂纹的转角(与二型破坏对应)沿着裂纹前缘从长半轴到短半轴的过程中是不断减小的，而裂纹的扭角(与三型破坏对应)沿着裂纹前缘则是不断增大的，值得注意的一点是，当Ψ=0°，即在裂纹的长半轴端点处时，裂纹的转角最大，而扭角为0，而当Ψ=90°时，裂纹的扭角最大，而转角则为0．

2 裂纹始裂状态应力强度因子

2.1 计算理论

Franc3d利用M积分计算应力强度因子，M积分可以写成：

M(1，2)=

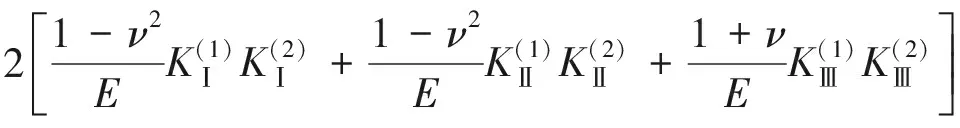
(6)

其中，M(1，2)为两种线性状态下的M积分，E为弹性模量，ν为泊松比，KⅠ为一型应力强度因子；KⅡ为二型应力强度因子；KⅢ为三型应力强度因子，(1)与(2)为两种线性状态．

2.2 始裂状态的应力强度因子分析

利用Franc3d软件对文献[13]中的椭圆裂纹进行计算，计算模型如图4所示，试件为5 cm×5 cm×10 cm的标准立方体试件，受单轴压缩荷载．图4(a)为试样的设计图，图4(b)为试样的计算网格图．

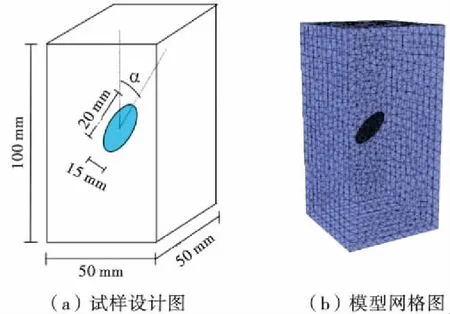
图4 计算模型

由于对称性，取裂纹前缘的1/4进行分析，定义无量纲化应力强度因子表达如下：

(7)

其中：

Q=1+1.464(a/b)1.65

(8)

式中，σ为模型边界上的应力，a为裂纹的长半轴长度，b为裂纹的短半轴长度．

图5为裂纹前缘长轴端点至短轴端点的一型与二型无量纲化应力强度因子分布．由图5可见，M积分计算所得的无量纲化二型应力强度因子与三型应力强度因子随裂纹前缘的变化规律与本文解析解计算所得的转角与扭角的规律一致，验证了本文解析解的正确性．

图5 应力强度因子分布

3 裂纹扩展计算

3.1 裂纹扩展理论

Franc3d采用最大周向拉应变准则计算裂纹扩展，裂纹起裂方向满足以下关系：

(9)

可以得出：

(10)

根据式(21)～(22)便可以计算出最大周向拉应变准则下的裂纹扩展方向．

3.2 计算结果

预制裂纹为倾角为60°的椭圆内裂纹，利用Franc3d进行单轴应力的施加，计算得到裂纹扩展过程，不同迭代步下的裂纹扩展过程如图6所示．

图6 单裂纹试件裂纹扩展过程

由图可见，单裂纹试件在双轴及不同内水压作用下首先在预制裂纹的上下尖端出现“翼型包裹状”裂纹，随着裂纹的逐渐扩展，裂纹所占面积越来越大，翼裂纹逐渐贯穿试件形成破坏．值得注意的是，当裂纹面扩展至试件边缘时，裂纹面会变平．

3.3 与现有试验结果对比

为说明数值模拟的合理性，将数值模拟结果与室内试验进行对比，付金伟[13]曾对高脆性透明树脂含椭圆内裂纹在单轴压缩下的裂纹扩展规律进行了室内试验，得到了裂纹的扩展规律及试件的破坏形态，本文将解析法的结果与数值模拟的结果与室内试验进行对比，室内试验典型试样的破坏形态及本文最终数值模拟结果如图7所示．

图7 室内试验与数值模拟结果对比

由图7可见，文献[13]室内试验预制裂纹在裂纹长轴定点处产生了翼裂纹，翼裂纹沿着最大主应力即加载方向扩展，最终形成贯穿型大裂纹，这与本文利用Franc3d软件进行数值模拟的结果一致，即本文利用M积分及最大周向拉应变准则可以很好的模拟三维内裂纹的扩展问题，同时注意到，预制裂纹靠近短轴端点处出现了“花瓣状”裂纹，这种裂纹形态的出现是由于裂纹面受到三型扭力所形成的，这与本文的解析分析结果及数值模拟分析的结果又具有一致性，即裂纹面在短轴端点处的三型应力强度因子最大．

4 结 论

1)基于椭圆裂纹尖端的应力状态，定义了应力集中系数函数δ，对应力集中系数函数δ求偏导计算出裂纹前缘每一点的转角θ和扭角Φ(分别对应裂纹的二型与三型破坏)随着裂纹前缘的变化规律，裂纹的转角沿着裂纹前缘从长半轴到短半轴的过程中不断减小，裂纹的扭角沿裂纹前缘不断增大．

2)基于M积分计算出了裂纹前缘的二型与三型应力强度因子的变化规律，与本文解析解计算所得的转角与扭角的规律一致．

3)基于最大周向拉应变准则得出了椭圆裂纹压载条件下的裂纹扩展规律，并与试验结果进行了对比，本文的解析规律及数值模拟规律与室内试验一致，验证了本文解析分析及数值分析的合理性．