基于可靠度理论研究导流洞涌水概率及敏感性
2019-11-23杨智翔马彤彤康家亮李保方
杨智翔,马彤彤,冯 伟,康家亮,李保方
(1.中水东北勘测设计研究有限责任公司,吉林长春130021;2.水利部长春机械研究所,吉林长春130021)
在导流洞建设过程中经常突发涌水问题,如构皮滩水电站导流洞蓄水后突发涌水,严重威胁洞室稳定性[1-2]。许多学者对导流洞的涌水量和涌水问题进行了研究,目前导流洞开挖过程中地下水的防渗问题还处于研究的初级阶段,地下洞室开挖过程中一旦突发涌水将给洞室稳定性及人身安全造成巨大威胁。张亮等[1]利用数值分析软件对白鹤滩水电站导流洞开挖过程中洞室的涌水量进行了分析。赵雪萍等[3]通过建立物理模型对导流洞的涌水进行了试验分析。黄宏伟等[4]对导流洞泄洪能力进行了分析,得到了影响导流洞泄洪能力的因素。但是以上研究均只考虑变异性指标对计算参数的影响,无法对洞室是否涌水进行预测,也无法说明预测结果的可靠程度。基于可靠度理论对导流洞的涌水概率进行分析,对实际工程安全有科学的指导意义。
笔者通过大井法将文得根水电站导流洞近似概化为带状大井[5-6],建立了可靠度判定导流洞涌水概率的分析方程及计算可靠度指标的方法。根据实地统计试验,对方程中导流洞岩体的渗透系数K、导流洞的开挖长度L、潜水面到含水层底板的水头H、洞室内排水沟的水深h、洞室的影响半径R等基本变量的变异性、均值与可靠度指标的变化规律进行研究,分析洞室涌水概率的可靠度指标对各参数的敏感性。
1 导流洞涌水量可靠度判定方法
1.1 临界状态方程
针对导流洞的渗水特点,建立其涌水量临界状态方程。由于导流洞开挖过程中在洞室内可以形成稳定的降落漏斗,因此将导流洞洞室简化为带状大井模型。引入渗流量 S(K,H,L,R) 和排水量 F(K,h,L,R) 两个基本变量,涌水量极限状态方程为

式中:Q为涌水量;K为岩体平均渗透系数;L为导流洞长度;H为潜水面到导流洞底板的水头高度;h为排水沟水深,排水沟布置于洞脸部位;R为导流洞的影响半径。
1.2 分布特征及变量分析
文得根水电站左岸导流洞平面见图1。库区地处山间盆地平原区,总体地势西高东低,两岸山体高程300~700m,绰尔河迂回曲折,河谷宽阔,为不对称的U形谷,坝址以上流域面积为12426km2,占总面积的72%,多年平均径流量19.5亿 m3,多年平均流量为61.8m3/s,该枢纽工程为一等大(1)型工程,主要永久建筑物级别为I级,经研究,选择初期导流标准为洪水重现期50a,相应的设计流量为32000m3/s。通过100次试验统计得到以上5个变量数据,绘制了每个变量的变化特征,见图2~图6。
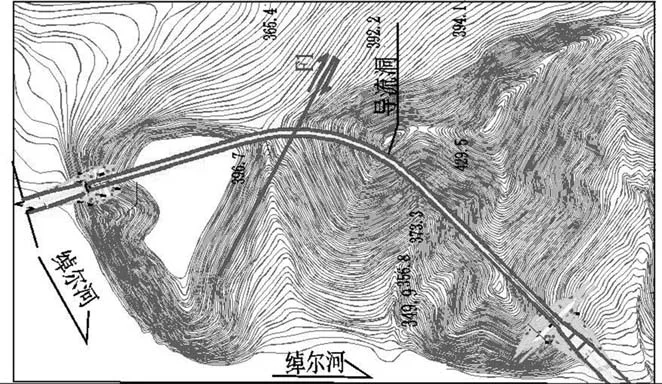
图1 导流洞平面
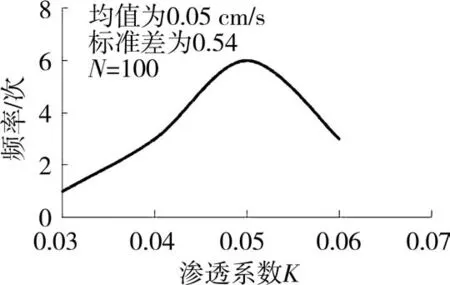
图2 导流洞岩体渗透系数统计分布特征

图3 导流洞长度统计分布特征
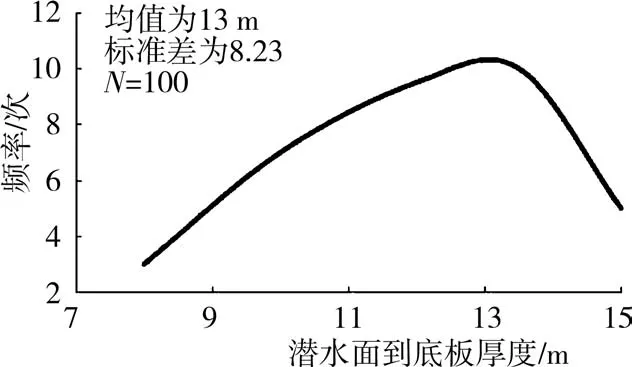
图4 潜水面到导流洞底板厚度统计分布特征

图5 排水沟水深统计分布特征
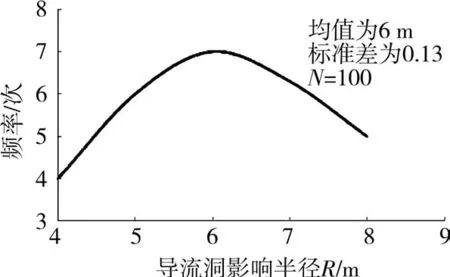
图6 导流洞影响半径统计分布特征
1.3 导流洞涌水可靠度指标及失效概率计算方法
令 Q=Q(K,L,H,h,R)= Q(X1,X2,X3,X4,X5)=0,则其上一点QX的均值E和标准差δ分别为
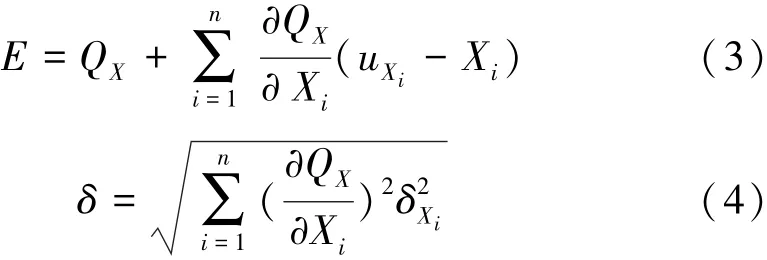
式中:uXi、δXi为影响QX点取值的各项变量的平均值和标准差;n为变量总数。
根据可靠度定义可得

式中:uk、uL、uH、uh、uR和 δk、δL、δH、δh、δR分别为渗透系数、导流洞长度、潜水面到底板水头、排水沟水深和导流洞影响半径的平均值和标准差。
令

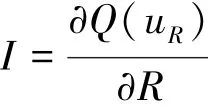
当Q=0时,有
坚持问题导向,聚焦区级馆服务能力不强、区域内公共文化资源缺乏整合、城乡公共文化服务发展不均衡等突出问题,坚持政府主导、改革创新、强化基层、实事求是的原则,大力推进公共图书馆总分馆制建设,为更好地满足广大群众基本文化需求创造良好条件,提供有力保障。

整理得

当 |αi+1-αi|≤容许误差时,取α =αi,失效概率Pf=1-φ(α),φ(α)为标准正态分布函数。根据导流洞涌水概率将导流洞涌水状态分为不涌水(Pf<5%)、涌水性差(Pf=5%~30%)、欠涌水(Pf=30%~60%)、基本涌水(Pf=60%~90%)、涌水(Pf>90%)。通过可靠度判定理论对国内具有代表性的水电站导流洞进行涌水概率分析,并与通过涌水量计算公式判定的涌水特征相互对比,两者对导流洞涌水特征的判定结果完全一样,见表2。
2 随机变量与可靠度指标的变化规律
2.1 渗透系数与可靠度指标敏感性的关系
为了探索导流洞岩体渗透系数均值和变异系数对涌水概率可靠度指标的敏感性,洞室内岩体渗透系数分别取均值 0.03、0.04、0.05、0.06、0.07、0.08,变异系数分别为 0.011 7、0.016 0、0.020 0、0.025 0、0.029 0、0.034 0,保持其他变量不变。
导流洞岩体渗透系数均值和变异系数可靠度指标见表3。由表3可知,可靠度指标随着导流洞岩体渗透系数的增大而减小,几乎为线性变化,递减速率Kk=0.6,此时最大失效概率增大,因此岩体渗透系数增大导致导流洞涌水可能性变大,这与实际情况相吻合。
可以看出:当岩体渗透系数均值增大时,可靠度减小;当变异系数增大时,可靠度虽然也减小,但幅度相对较小,而此时最大失效概率增大。通过比较得出:导流洞涌水的可靠度对岩体渗透系数均值敏感性较大。
2.2 导流洞长度L与可靠度指标敏感性的关系
导流 洞 长 度 均 值 取 368、568、768、968、1 168、1 368 m,变异系数取 0.120 0、0.170 0、0.212 0、0.252 0、0.302 0、0.362 0,在确保其他变量恒定的情况下,探索导流洞长度与可靠度指标敏感性的关系。

表3 导流洞岩体渗透系数均值和变异系数的可靠度指标
导流洞长度均值和变异系数的可靠度指标见表4。由表4可知,当洞室长度均值增大时,其可靠度指标减小,最大失效概率增大,随着导流洞长度均值的增大,导流洞涌水概率不断增大,随着变异系数的不断增大,可靠度指标减小幅度非常明显。综上,可靠度指标对导流洞长度的变异系数敏感性比较高。

表4 导流洞长度均值和变异系数可靠度指标
2.3 潜水面到导流洞底板的水头与可靠度指标敏感性的关系
潜水面到导流洞底板的水头均值取9、11、13、15、17、19 m,变异系数取 0.202 7、0.251 2、0.321 1、0.372 4、0.423 0、0.538 9,在确保其他变量恒定的情况下,潜水面到导流洞底板水头均值和变异系数可靠度指标见表5。

表5 潜水面到导流洞底板水头均值和变异系数可靠度指标
从表5可以看出,当潜水面到导流洞底板水头均值增大时,其可靠度指标递减,失效概率递增。因此,可以得出随着潜水面水头的增大,洞室涌水概率增大,洞室稳定性下降。变异系数增大使可靠度增大,但增大较慢,基本保持不变,因此对于导流洞来说,可靠度指标对潜水面到导流洞底板的水头敏感性比较高。
2.4 排水沟水深与可靠度指标敏感性的关系
排水沟水深均值取 5、7、9、11、13、15 m,变异性系数取 0.101 2、0.132 3、0.158 3、0.201 4、0.245 5、0.300 2,其他变量保持不变,对应可靠度指标见表6。
从表6可以得出,当排水沟水深均值增大时,可靠度指标递增,而此时失效概率递减,递减速率为0.014,因此可以推测当排水沟水深增大时,导流洞的涌水概率减小,洞室更稳定。变异系数增大导致可靠度增大,然而增大速率较慢,变化不明显。综上,从导流洞的角度分析,可靠度指标对排水沟的水深更敏感。

表6 排水沟水深均值和变异系数可靠度指标
2.5 导流洞影响半径与可靠度指标敏感性的关系
在保持其余变量不变的情况下,洞室的影响半径均值取 4、5、6、7、8、9 m,变异系数取 0.130 0、0.173 2、0.189 8、0.253 2、0.292 0、0.348 2。 导流洞影响半径均值和变异系数可靠度指标见表7。
从表7可以得出,当洞室影响半径均值增大时,可靠度指标递增,这时失效概率递减,因此可以推测当导流洞影响半径增大时,导流洞的涌水概率减小,洞室更稳定。变异性系数增大导致可靠度增大,然而增长速率较小,因此可靠度指标对导流洞影响半径的敏感更高。

表7 导流洞影响半径均值和变异系数可靠度指标
3 结 论
(1)通过对国内典型导流洞的统计分析得出了导流洞岩体渗透系数、导流洞长度、潜水面到导流洞底板的水头、排水沟的水深、导流洞的影响半径均符合正态分布。
(2)随着排水沟水深、导流洞影响半径的增大,导流洞涌水的可靠度指标越来越大,洞室更趋于稳定;随着岩体渗透系数、导流洞长度、潜水面到导流洞底板水头的增大,导流洞涌水的可靠度指标基本线性减小,洞室更不安全。
(3)综上所述,首先可靠度指标对岩体渗透系数的敏感性最高,对洞室涌水概率影响最大,其次是潜水面到导流洞底板的水头,最后是导流洞的长度和影响半径,而排水沟的水深对洞室涌水可靠度指标影响不明显,因此在治理工程中要合理判断岩层渗透系数变化。
