A Matrix Representation of Outer Derivations from gl0|2 to the Generalized Witt Lie Superalgebra

Zheng Ke-li

(Department of Mathematics, Northeast Forestry University, Harbin, 150040)

Communicated by Du Xian-kun

Abstract: Let gl0|2 be a subalgebra of the general linear Lie superalgebra. In this paper, outer derivations from gl0|2 to the generalized Witt Lie superalgebra are completely determined by matrices.

Key words: outer derivation; inner derivation; matrix representation; generalized Witt Lie superalgebra

1 Introduction

The non-inner derivations are called outer derivations, which are in fact equal to the first cohomology groups of (super)algebras under consideration. For Lie (super)algebras, the existence of outer derivations have been well investigated (see [1]–[5] for examples). During the past half century, the theory of outer derivations and first cohomology groups for modular Lie (super)algebras has developed in a variety of directions and a large number of results have been obtained (see [6]–[8] for example). For classical Lie superalgebras over a field of prime characteristic, the recent papers [9] and [10] computed low-dimensional cohomology groups of the special linear Lie superalgebra slm|nand its subalgebra A(1; 0) with coefficients in Witt or special superalgebras by virtue of the direct sum decomposition of submodules and the weight space decompositions of these submodules relative to their standard Cartan subalgebra.

The original motivation for this paper comes from [11]. The treatment of linear superal-gebras necessitates matrix computational techniques which are set forth in [12]. This paper contains a considerable amount of computation and determines the outer derivations from gl0|2to the generalized Witt Lie superalgebra W. Section 2 reviews the necessary notions.Section 3 calculates derivations and inner derivations from gl0|2into each irreducible submodule of W over a field of prime characteristic. Therefore, outer derivations from gl0|2to W are determined. In Section 4, the outer derivations from gl0|2to W over a field of characteristic zero are considered. Throughout this paper F is assumed to be an arbitrary field. The set of positive integers and the set of nonnegative integers are written as N+and N, respectively. Let L be a Lie algebra over F and A be an arbitrary L-module. Let x ∈L,a ∈A, we denote by x · a the element x acts on a.

2 Preliminaries

An F-linear mapping φ: L →A is called a derivation from L into A if

Denote by Der(L, A) the derivation space from L into A. A derivation ψa: L →A is called inner if there is a ∈A such that

Denote by Ider(L, A) the inner derivation space from L into A. Denote by Oder(L, A) the outer derivation space from L into A. Thus

This implies that the first cohomology group H1(L, A) is isomorphic to Oder(L, A).

The following lemma is a standard fact. For more details see [13].

Lemma 2.1Suppose thatAis anL-module andA1, A2, ··· , Akare submodules ofAsuch thatA = A1⊕A2⊕··· ⊕Ak.Then

According to Lemma 2.1, we obtain

which is frequently used in the sequel.

For sake of simplicity, let m, n denote fixed integers in N+ {1, 2}. For α = (α1, ··· ,αm) ∈Nm, we put

LetΛ(n) be the exterior superalgebra over F in n variables ξ1, ξ2, ···, ξnand O(m, n, t)denote the tenser product O(m,) ⊗FΛ(n).

where

Put Y0:= {1, 2, ·· · , m} and Y1:= {1, 2, ·· · , n}. Set

and

where B0:= ∅. For u = 〈i1, i2, ··· , ik〉 ∈Bk, set |u| := k, |∅| := 0, ξ∅:= 1, ξu:=ξi1ξi2··· ξikand ξE:= ξ1ξ2··· ξn. If u ∈Bk, j ∈{u}, then {u − 〈j〉} := {u} {j} ∈Bk−1.Let u(j) = |{l ∈{u} | l < j}|. If j ∈Y1{u}, then we put u(j) = 0 and ξu−〈j〉= 0. Clearly,constitutes an F-basis of O(m, n,).

Let D1, ··· , Dm, d1, ··· , dnbe linear transformations of O(m, n,) and εi:= (δi1, ···,δim) such that

where δijis Kronecker delta defined by δij= 1 if i = j and δij= 0 otherwise. Set

Then W is the generalized Witt Lie superalgebra over a field F of prime characteristic,which is contained in Der(O(m, n,)). In particular, it is a finite-dimensional simple Lie superalgebra (see [14]). Clearly, W possesses a standard F-basis

From this vector space basis, one can read off that

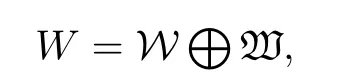
where

A verification shows that gl0|2is in fact a Lie algebra which is isomorphic to the subalgebra 〈ξidj| i, j = 1, 2〉 of W. Then W can be regarded as a gl0|2-module by means of the adjoint representation. Thus it makes sense to consider the outer derivation Oder(gl0|2, W)of gl0|2with coefficients in W.

3 Oder(gl0|2, W) in Prime Characteristic

In this section, we deal with Oder(gl0|2, W) in prime characteristic.

Hereafter, let α be an element of A(m,), k be an element of Y0, u, v be members of set B and {ξidj| i, j = 1, 2} as a basis of gl0|2. Since x(α)has no effects under the adjoint operation of gl0|2, it will be omitted in the following proofs. For any ai, bj∈F and i, j ∈{1, 2, 3, 4}, the matrix is written as follows.

For i ∈Y1, it suffices to consider Oder(gl0|2, Wi) and Oder(gl0|2, Wi). On the one hand,we deal with the outer derivations Oder(gl0|2, Wi).

Proposition 3.1Oder(gl0|2, W0) = 0.

Proof.A verification shows that [x, W0] = 0 for every x ∈gl0|2. If φ is a derivation from gl0|2into W0, then φ = 0, i.e., Der(gl0|2, W0) = 0. The proof is completed.

Proposition 3.2The matrixAis a matrix representation ofOder(gl0|2, W1)ofgl0|2with coefficients inW1,where

Proof.Recall that W1= 〈ξiDk〉 for i ∈Y1. It suffices to consider Der(gl0|2, 〈ξiDk〉) and Ider(gl0|2, 〈ξiDk〉). Since [x, ξiD1], [x, ξiD2], ···, [x, ξiDm] are all equal to [x, ξiDk] for x ∈gl0|2, we denote ξiD1, ξiD2, ···, ξiDmby ξiDk, i ∈Y1.

(i) The derivation space from gl0|2into 〈ξiDk| i ∈Y1〉.

Suppose that

is a derivation from gl0|2into 〈ξiDk| i ∈Y1〉, where cij∈F, i ∈{1, 2, 3, 4}, j ∈Y1. By replacing x and y with the standard basis of gl0|2in Eq. (2.1), we have

(3.1) implies that

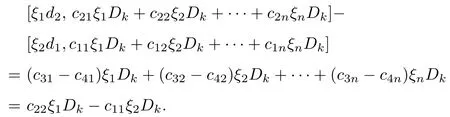
A comparison of coefficients yields

Analogously, (3.2)–(3.6) show that

Therefore,

where c11, c22, c33, ···, c3n∈F.

(ii) The inner derivation space from gl0|2into 〈ξiDk| i ∈Y1〉.

By the definition of inner derivation, elements of {ψξiDk| i ∈Y1} are as follows:

Hence

Combining (i) and (ii), the proof is completed.

Proposition 3.3Oder(gl0|2, Wi) = 0, i ∈Y1.

Proof.Recall that W2= 〈ξiξjDk| i, j ∈Y1, i < j〉. In the case of i, j ∈Y1{1, 2}, we have[x, W2] = 0 for any x ∈gl0|2. Suppose that φ is a derivation from gl0|2into W2. Then we can easily prove φ = 0. For i ∈{1, 2}, Der(gl0|2, W2) and Ider(gl0|2, W2) are considered,respectively.

Suppose that

is a derivation from gl0|2into W2, where cij, bit∈F, i ∈{1, 2, 3, 4}, j ∈Y1 {1} and t ∈Y1{1, 2}. As

we have (3.1)–(3.6). By a comparison of coefficients, we have

Then

Der(gl0|2, W2)

where c13, ···, c1n, c32, ···, c3n∈F.

Using the methods in the proof of Proposition 3.2, we obtain inner derivation space from gl0|2into W2as follows:

Ider(gl0|2, W2)

where c13, ···, c1n, c32, ···, c3n∈F. Above all, they show that

so

It follows that Oder(gl0|2, Wi) = 0, i ∈Y1from induction on i.

Now the following theorem is a direct consequence of (2.2) and Propositions 3.1–3.3.

Theorem 3.1The matrixAdetermines the outer derivationOder(gl0|2, W)ofgl0|2with coefficients inW,where

On the other hand, the outer derivations Oder(gl0|2, Wi) for all i ∈Y1are calculated.Similarly, by methods employed in Proposition 3.2, the following results may be verified.

Proposition 3.4The matrixBis a matrix representation ofOder(gl0|2, W0),where

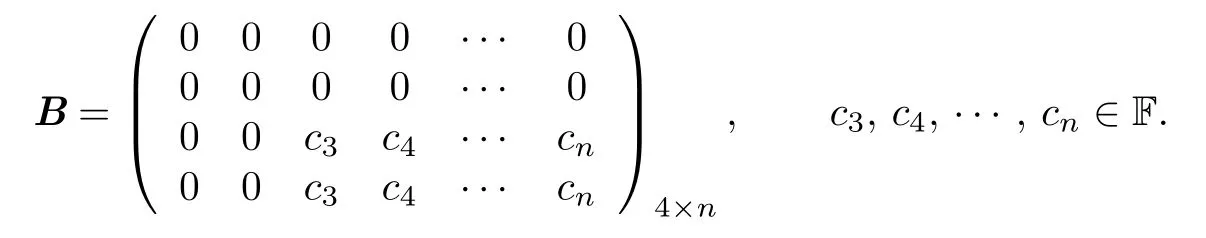
Proof.Applying the methods of Proposition 3.2, we consider Der(gl0|2, W0) and Ider(gl0|2, W0), where W0= 〈dl| l ∈Y1〉.

(i) The derivation space from gl0|2into W0.

Suppose that

is a derivation from gl0|2into W0, where cij∈F, i ∈{1, 2, 3, 4}, j ∈Y1. For any x, y ∈gl0|2,the identity φ([x, y]) = [x, φ(y)] −[y, φ(x)] yields (3.1)–(3.6). A comparison of coefficients shows that

where t ∈Y1{1, 2}. Then

where c12, c21, c33, ··· , c3n∈F.

(ii) The inner derivation space from gl0|2into W0.

Using the methods in the proof of Proposition 3.2, we obtain that

where a, b ∈F.

Combining (i) and (ii), the result follows.

By similar methods as in Propositions 3.2–3.4, we have

Proposition 3.5The matrixCis a matrix representation ofOder(gl0|2, W1), where

Proposition 3.6Oder(gl0|2, Wn) = 0.

Hereafter, we denote the combinatorial numberby, where m ≤n.

Proposition 3.7The matrixD2is a matrix representation ofOder(gl0|2, W2)ofgl0|2with coefficients inW2,where

Corollary 3.1Fori ∈Y1 {1, n}andc ∈F,the matrixDiis a matrix representation ofOder(gl0|2, Wi),where

Proof.The result may be proved by induction on i.

Theorem 3.2If(B|C|D2|···|Dn−1)is a block matrix with subblocksB, C, D2, ··· ,Dn−1as in Propositions3.4, 3.5and Corollary3.1,then(B|C|D2|···|Dn−1)is a matrix representation of the outer derivationOder(gl0|2, W)ofgl0|2with coefficients inW.Proof.This is a direct consequence of (2.2), Propositions 3.4–3.7 and Corollary 3.1.

Theorem 3.3If(A|B|C|D2|···|Dn−1)is a block matrix with subblocksA, B, C, D2,··· , Dn−1as in Theorem3.1,Propositions3.5, 3.5and Corollary3.1,then(A|B|C|D2|···|Dn−1)is a matrix representation of the outer derivationOder(gl0|2, W)ofgl0|2with coefficients inW.

Proof.This is a direct consequence of (2.2), Theorems 3.1 and 3.2.

4 Oder(gl0|2, W) in Characteristic Zero

Imitating the situation that the generalized Witt Lie superalgebra W over a field F of characteristic zero (see [15], [16]), the elements of F[x1, ·· · , xm] have no effects under the adjoint operation of gl0|2. So Oder(gl0|2, W) in characteristic zero can be obtained by the same methods as in prime characteristic. Therefore, we have

Theorem 4.1LetA, B, C, Di, W1, W0, W1, Wias in Theorem3.3andFbe the underlying base field of characteristic zero. Then(A|B|C|D2|···|Dn−1)is a matrix representation of the outer derivationOder(gl0|2, W)ofgl0|2with coefficients inW.