Expanders, Group Extensions, Hadamard Manifolds and Certain Banach Spaces
2019-11-22ShanLin
Shan Lin
(Faculty of Natural Sciences, University of Puerto Rico, Rio Piedras Campus,San Juan, 00925, Puerto Rico)
Communicated by Gong Gui-hua
Abstract: In this note, we prove that expanders cannot be coarsely embedded into group extensions of sequences of groups which are coarsely embeddable into Hardamad manifolds and certain Banach spaces due to the similar concentration theorems.
Key words: expander; group extension; Hadamard manifold; Banach space
In [1], Arzhantseva and Tessera proved the property that expanders cannot be coarsely embedded into group extensions of sequences of groups which are coarsely embeddable into Hilbert spaces. In this note, we show that this property also holds for Hadamard manifolds and Banach spaces whose unit balls are uniformaly embeddable into Hilbert spaces.
First, let us recall basic definitions of expanders (see [2] for more information and for references). Let (V, E) be a finite graph with the vertex set V and the edge set E. Denote the cardinality of V and E by |V | = n and |E| = m. We also define an orientation on E.The differential d : ℓ2(V ) → ℓ2(E) is defined by

for all f ∈ ℓ2(V ) and e = (e+, e−) ∈E, where e+and e−are initial and end points of e,respectively.
This differential d is an m×n matrix. The discrete Laplace operator ∆= d∗d, where d∗is the adjoint operator of d. This definition does not depend on the choice of the orientation of E. ∆is self-adjoint and positive. Hence it has real nonnegative eigenvalues. Denote by λ1(V ) the minimal positive eigenvalue of the discrete Laplace operator ∆of the graph(V, E).
Definition 1A(k, λ)expander is a graph(V, E)with a fixed degreekandλ1(V ) ≥ λ.A sequence of graphs(Vn, En)of a fixed degreekand with|Vn| →∞is called an expanding sequence of graphs if there is a positive constantλsuch thatλ1(Vn) ≥ λfor alln ∈N.
Let X and Y be metric spaces and let f : X →Y be a map. Define the Lipschitz constant of f by

Lemma 1IfXis a graph,then
Lip(f) = sup {d(f(s), f(t)) : s, t ∈Xare adjacent}.
Proof.Let
Lip1(f) = sup {d(f(s), f(t)) : s, t ∈X are adjacent}.
Clearly Lip1(f) ≤Lip(f). For any pair s, t ∈X with d(s, t) = n, there exists a sequence of points x0, x1, ··· , xnof X such that x0= s, xn= t and xi, xi+1are adjacent for all i = 0,··· , n −1. Then

Therefore, Lip(f) ≤Lip1(f). The proof is done.
Hence, for any pair (s, t) ∈G, one always has
d(f(s), f(t)) ≤Lip(f)d(s, t).
In [4], we have the following concentration theorem.
Theorem 1[4]LetMbe a Hadamard manifold with bounded sectional curvatures. And let(V, E)be a(k, λ)expander. Then there existsR > 0such that for anyf : V →M,

wheremis a point such that
In the following proposition, we see that if the average value is bounded by a number,then at least half of summands are bounded by the twice of the preceding number.
Proposition 1Leta1, ··· , anbe non-negative real numbers anda > 0. If
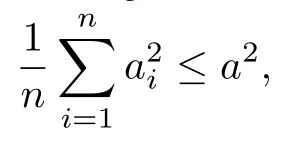
then there are at leastofa1, ··· , anless than or equal to2a.
Proof.Assume that this is false. Then there are at least k numbers ai1,··· , aiksuch that aij> 2a and k ≥. Then

which contradicts the hypothesis of the proposition

Corollary 1Under the assumption of the previous theorem,there is a subsetAofGanda pointg ∈Gsuch that|A| ≥|G|and the points ofAare mapped at distance at most4R ·(Lip(f)+ 1)fromf(g).
Proof.By the previous theorem and the proposition, choosing av= ∥f(v) −m∥for v ∈G and a = R ·(Lip(f)+ 1), there is a subset A of G such that


The proof is done.
Based on the concentration theorem and corollary, we now prove our main theorem.
Theorem 2LetZbe a Hadamard manifold with bounded sectional curvatures,and let(Gn)n∈Nbe a sequence of finitely generated groups equipped with finite generating setsSnof sizek. We assume that for everyn,there is an exact sequence

such that
(1)the sequence(Nn)n∈Nequipped with the induced metric coarsely embeds intoZ;
(2)the sequence(Qn)n∈Nequipped with the word metric associated to the projectionTnofSncoarsely embeds intoZ.
Then,given a numberK > 0,an expander(Xn)n∈N,and a sequence ofK-Lipschitz mapshn: Xn→Yn= (Gn, Sn),there exists a constantc > 0and a sequenceyn∈Ynsuch that the cardinality of({yn})is at leastc|Xn|,and its diameter is not less thanc diam(Xn).
Proof.By the hypothesis, there are two maps ϕn: (Nn, dSn) →Z and ψn: (Qn, dTn) →Z and two proper functions ρ−, ρ+: [0, ∞) →[0, ∞) with the property that for all n ∈N and all x, y ∈Nn,

and

Let λ > 0, d be such that for all n, Xnis a (d, λ)-expander.
Assume that hn: Xn→Gnare K-Lipschitz maps. Let πndenote the projection map from Gnto Qnfor n ∈N. Clearly πnis always 1-Lipschitz. We define the composition fn:= ψn◦ πn◦hn: Xn→Z. The metric space Qnis equipped with the graph metric, so ψn: Qn→Z has the Lipschitz constant
Lip(ψn) = sup {d(ψn(s), ψn(t)), where s, t ∈Qnare adjacent}.
Since

for x, y ∈Qnand dTn(s, t) = 1 if s, t are adjacent in Qn,

By the composition, {fn: Xn→Z}n∈Nis a sequence of Kρ+(1)-Lipschitz maps. Applying Corollary 1 for each Xn, there exist xn∈Xnand a subset An⊆Xnwith |An| ≥such that fn(An) ⊂B (fn(xn), 4R(Kρ+(1)+ 1)). By the properness of ρ−, it implies that πn◦hn(An) ⊂B(πn◦hn(xn), r), where r =(4R(Kρ+(1) + 1)) is independent of n. As in the hypothesis, Gnhas the generating set Snof size k and Qnis equipped with the word metric associated to the projection Tnof Sn, the cardinality |B(πn◦hn(xn), r)| ≤kr. Hence there is a subsetof Anof with || ≥≥whose image πn◦hn() is one point in Qn. Therefore, hn() belongs to a coset of Nnin Gn. Composing hnby a proper left translation in Gn, without loss of generality we may assume that hn() ⊂Nn.
Next we repeat the preceding process. Consider the composition

With the similar estimation, Lip(gn) ≤Kρ+(1). Applying Corollary 4 to the map gn, there exist sequences yn∈andwith || ≥, such that

We conclude that, by the properness of ρ−, hn() ⊆B(hn(yn), r), where

Hence, there exists a subsetofwith

which is mapped by hnto one point. This proves our theorem.
In [3], Ozawa showed the following concentration theorem.
Theorem 3[3]LetXba a Banach space whose unit ball is uniformly embeddable into a Hilbert space. Then,for anyk ∈Nandh > 0,there exists a positive numberR = R(k, h, X)which satisfies the following:for any mapffrom a(k, h)-expanderGintoX,we have

whereis the mean off.
With the similar proof, we can have the result for Banach spaces.
Theorem 4LetZba a Banach space whose unit ball is uniformly embeddable into a Hilbert space, and let(Gn)n∈Nbe a sequence of finitely generated groups equipped with finite generating setsSnof sizek. We assume that for everyn,there is an exact sequence

such that
(1)the sequence(Nn)n∈Nequipped with the induced metric coarsely embeds intoZ;
(2)the sequence(Qn)n∈Nequipped with the word metric associated to the projectionTnofSncoarsely embeds intoZ.
Then,given a numberK > 0,an expander(Xn)n∈N,and a sequence ofK-Lipschitz mapshn: Xn→Yn= (Gn, Sn),there exists a constantc > 0and a sequenceyn∈Ynsuch that the cardinality of({yn})is at leastc|Xn|,and its diameter is not less thanc diam(Xn).
杂志排行
Communications in Mathematical Research的其它文章
- The Homotopy Perturbation Renormalization Group Method to Solve the WKB Problem with Turn Points
- A Matrix Representation of Outer Derivations from gl0|2 to the Generalized Witt Lie Superalgebra
- Univalent Criteria for Analytic Functions Involving Schwarzian Derivative
- Third Hankel Determinant for the Inverse of Starlike and Convex Functions
- A Note on the Stability of K-g-frames
- The Existence of Weak Solutions of a Higher Order Nonlinear Eilliptic Equation
