基于DEA/PCA 模型的中国工业产业经济效率评价

刘志鹏

（贵州大学，贵州 贵阳 550025）

一、引言

我国工业产业共41 个行业，每种行业都拥有多个投入、产出要素，通过这些指标我们无法直观地看出各行业的投入产出比以及它们的排序。常规办法可以用数据包络分析（DEA）方法对这些产业的投入与产出指标进行相对评价，但是却无法对这些产业进行相对排序。另一种方法是主成分分析（PCA），该方法能够对评价对象进行排序，但是却无法反映投入产出综合比[1]。为了将两种方法的优点结合起来，本文尝试构造DEA 和PCA相结合的分析方法，综合评价我国工业产业各行业的经济现状。

二、工业产业结构及其投入产出指标体系

根据2018 年1 月8 日发布的国家统计局新国民经济行业分类，我国工业产业分为采矿业、制造业和电力、燃气及水的生产和供应业三个大类，这三个大类又细分为41 个行业。

工业产业的投入与产出要素很多，本文选取的3 个投入要素是这些行业的大中型企业的固定资产合计、流动资产合计以及平均用工人数，选取的4 个产出要素是这些行业的大中型企业的所缴增值税、个人所得税、应收账款净值、销售产值。根据2015 年《中国统计年鉴》和《中国工业统计年鉴》数据，得到了本文工业产业投入产出数据结构，其中其他采矿业由于各项数据较小，特别是各平均用工人数少于100 人，因此我将这一行业从表格中忽略。

三、DEA/PCA 评价模型

该模型参考杜纲，郭均鹏，张建国，金玉申以及王海峰等学者的构建方式。

（一）DEA 数学模型求解与分析

DEA 模型即（CR2模型）：

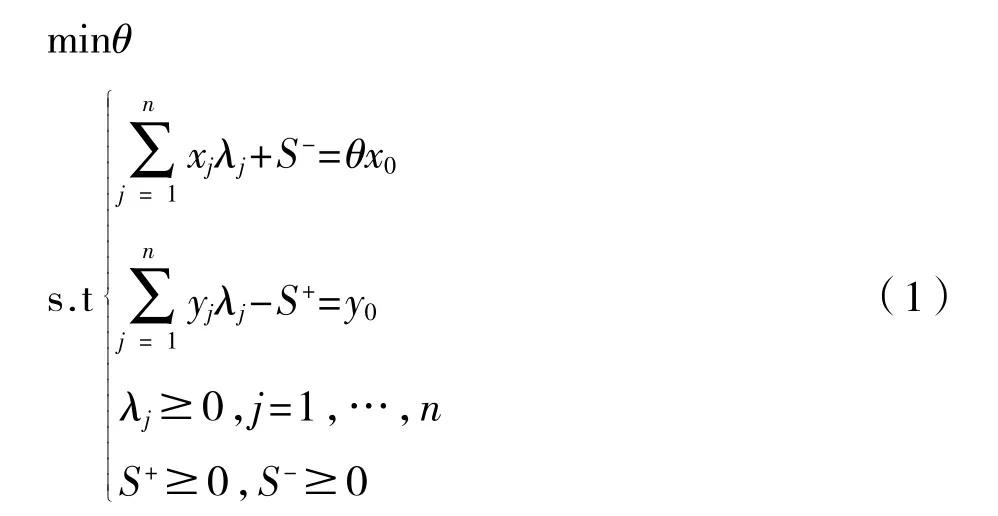
此为相应于第j0产业的DEA 模型，其中S+和S-为松弛和剩余向量[2-5]。

求解以上方程，能够得到每个行业的θ，λj，S+和S-。θ值代表该行业的相对有效性，取值范围为0<θ≤1。当θ=1，并且S+=S-=0 时，此时为最优解，那么该j 行业就是DEA 有效的；若θ越趋近于0，那么该j 行业相对有效性就越差[2]。但是该模型的缺点就是无法对θ=1 的行业进行排序。

此外，求解出来的λj代表该行业的规模报酬。当时，该行业的规模报酬是不变的，该行业规模不用调整；当时，说明该行业的规模报酬是递减的，因此要缩小该行业的产业规模；当时，该行业的产业规模偏小，规模报酬是递增的，未来需要扩大产业规模。对于该行业的投入产出量的调整值如公式（2）所示。

（二）PCA 数学模型求解与分析

首先将工业各产业的数据换算成我们需要的指标，定义指标为：

其中，i，r，j，k 分别表示投入指标、产出指标，产业的下标，各产业的比率指标的下标，本文中i=1，2，3，r=1，2，3，4，j=1，2，…，40，k=1，2，…，12。

本文样本数据为40 个行业的12 个比率值，将样本数据进行主成分分析，选取前m 个主成分（贡献率大于等于85%），建立评价模型。

其中，n=1，2，…，m；ain表示第i 个因子在第n个主成分评价模型中的得分系数；pin表示第i 个因子在第n 个主成分中的载荷值；λn表示第n 个主成分的特征值。

如公式（4）所示，该综合评价模型基于m 个主成分建立，权重为每个主成分的特征值占所有主成分特征值综合的比率。

同时，开设客观评标分值体系，采用综合评分法，可以根据维保标的物的实际情况，设置不同评审要素，如维修工程师资质、经验、用户评价和PDCA记录等客观指标，“从而最大程度减少对投标人维保方案的主观判断，避免投标人仅因文件做得好的印象分中标。”

（三）DEA/PCA 综合评价模型

通过DEA 方法计算出的θ值，PCA 方法求出相应的p 值并最终求出各产业对应的F 值，结合两种方法对各行业进行排序和对比。针对CR2模型无法对DEA 有效的行业进行排序这个缺陷着重分析，也就是若两个行业DEA 有效，而PCA 评价结果不同，根据结果，这两个行业规模和技术均是有效的，但是在各产业投入产出差异的综合指标却能得出两个行业的排序。而且，还可以通过各项因子进一步分析，得出需要改进的行业方向。

除此之外，还可以通过将数据做成二位坐标图，更为直观的进行分析。如图1 所示，横轴为DEA 评价值，纵轴为PCA 评价值，同时横轴以0.7为界，纵轴以0 为界，将横轴和纵轴划分为低、高部分。各产业根据不同的DEA、PCA 评价值标示在这个坐标图中，从而被区分在4 个区域，即A、B、C、D 四个区域。这样就可以清晰、直观地将各行业的相对有效性进行对比与分析。

图1 DEA/PCA 坐标屏幕

A 区域为“双高”区域，落在该区域的产业无论DEA 评价值还是PCA 评价值都是“高水准”的，特别是处于坐标图右边界的产业，这些产业DEA 评价值为1，而且差异最大的投入产出比综合指标也处于高水平，相对绩效及其优异。

处于B 与C 区域的产业均有一项评价值较高，另一项评价值较低。比如说B 区域，该区域的产业DEA 相对有效性相对较高，而在异最大的投入产出比综合指标上得分较低。C 区域与此相反。这两个区域的产业就要进行综合分析进行取舍，根据产业具体情况来判断哪个评价值更有效。一般来说，DEA 的评价值一般要优先于PCA 评价值，因此，这里认为B 区域的产业要优于C 区域的产业。

D 区域的产业，DEA 和PCA 评价值都比较低，也就是说产业的相对有效性较差，异最大的投入产出比综合指标的分也很低。该区域的产业属于需要加以改进或者需要淘汰的产业。

因此，对于A、B、C、D 四个区域评价依次对应为优、良、中、差，对于同一区域的产业，可以根据具体位置的横纵坐标的进行排序，从而进一步评价与分析。

四、中国工业产业经济DEA/PCA 评价与分析

（一）中国工业产业经济PCA 评价

对统计数据进行主成分分析，其结果如表1所示，前四项因子的累计贡献率为92.202%，超过了85%，因此认为这4 个成分足以概括大部分信息（m=4）。

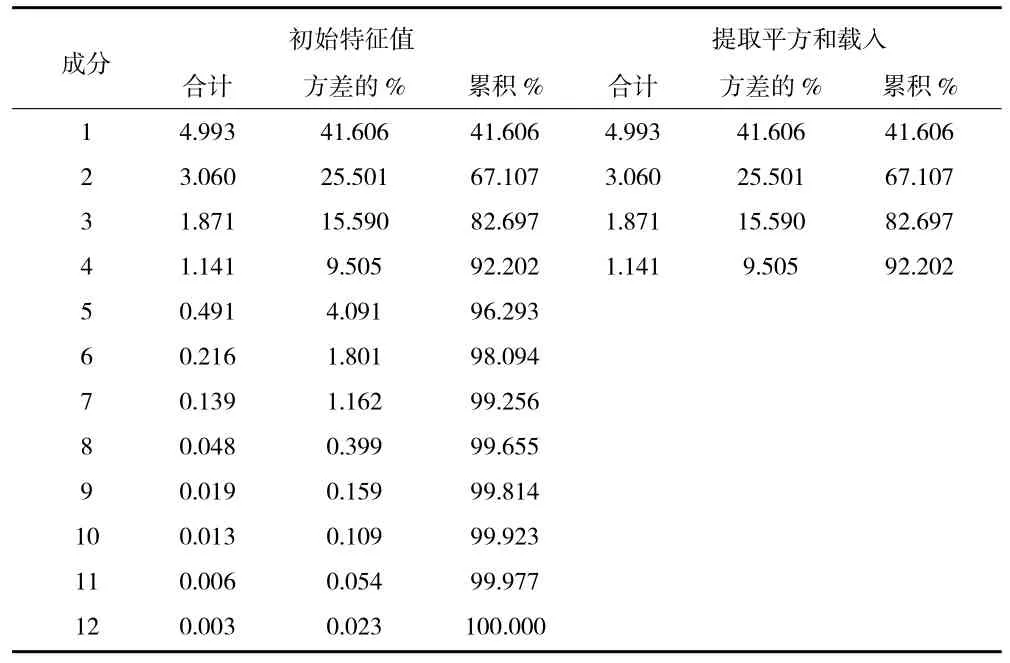
表1 解释的总方差

由此可以得出公式（5）的具体形式：

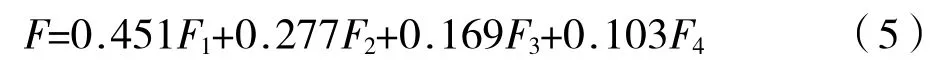
将具体数值的（3）、（4）代入（5）即可得到各产业的PCA 综合评分[6]。

表3 为通过主成分分析模型得出的中国工业各行业的产业得分值和排名。

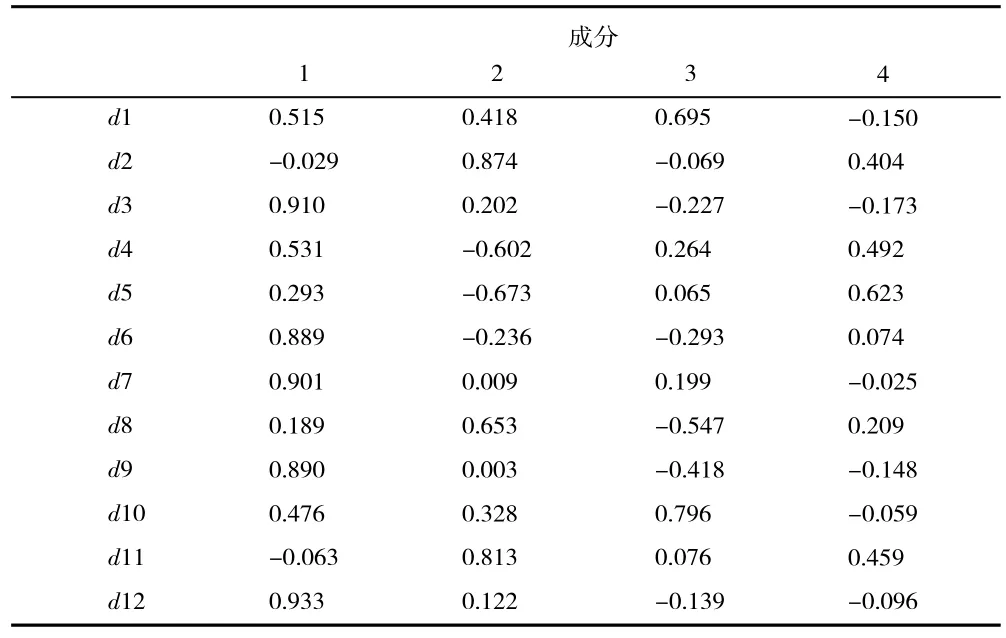
表2 成分矩阵 a

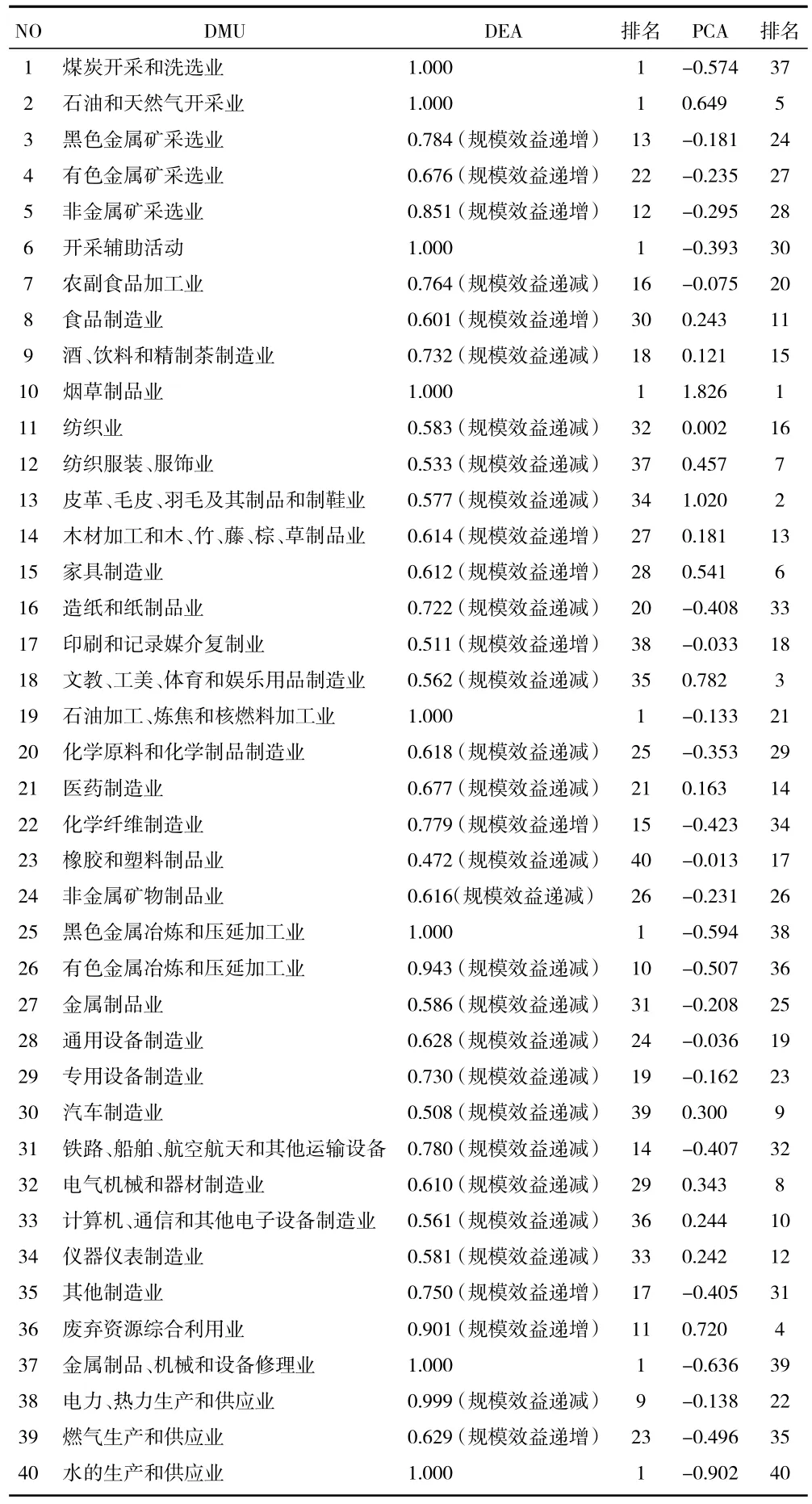
表3 中国工业产业的DEA 法和PCA 法评价结果

（二）中国工业DEA 评价

利用DEA 方法，对我国工业产业的40 个行业进行评价的结果如表3 所示。

如果DEA 与PCA 这两种评价方法得出的结果差异性过大，那么两者综合分析也就没有意义[7]。因此，这里采用符号检验法来对DEA 和PCA 两种排序方法进行差异性检验。记zi（i=1，…，40）为i 产业的DEA 和PCA 评价的排序之差，n1是zi>0的个数，n2是zi<0 的个数，n=n1+n2=38。符号检验表的临界值是S0.05（38）=12，min（n1，n2）=18>12。说明DEA 和PCA 两种排序方法的结果无显著差异。

（三）中国工业产业经济DEA/PCA 综合分析

利用表4 中各产业的DEA 和PCA 分值，得到了中国工业40 个行业在DEA/PCA 坐标屏幕中的分布，如图2 所示，为了各产业的散点图能在坐标中更清楚地表示，图2 用数字代替了各产业的实际名称。以下行业均用数字代替行业名称。

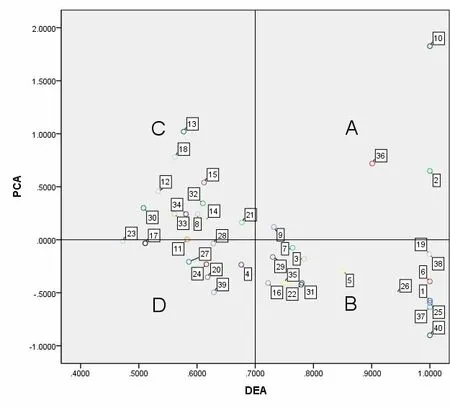
图2 中国工业产业DEA/PCA 综合评价

通过图2 可以看出，处于A（高水平）区域的产业包括2、9、10、36。说明在中国工业产业中，这4 个产业的相对有效性为优，是具有低投入、高产出特点的高效性产业，特别是9 酒、饮料和精制茶制造业以及10 烟草制品业，属于高端消费品行业，利润非常高，这与客观事实相符。处于B 区域的产业包括1、3、5、6、7、16、19、22、26、29、35、37、38、40，这些产业大多是重工业，其中1 煤炭开采和洗选业、19 石油加工、炼焦和核燃料加工业、37 金属制品、机械和设备修理业、40 水的生产和供应业这4 个产业θ=1，是低投入、高产出的高有效性产业，但是在差异最大的投入产出比综合指标上得分很低，所以其评价为良。C 区域包括8、11、12、13、14、15、18、21、30汽车制造业、32、33、34，在这区域的产业大多是轻工业和高技术产业，这些产业相对有效性评价为中，虽然DEA值较低，但是差异最大的投入产出比综合指标上得分较高。处于D 区域的有4、17、20、23、24、27、28、39，在这个区域大多是落后产能，这些产业是高投入、低产出的低有效性产业。其中4 有色金属矿采选业、23 橡胶和塑料制品业、39 燃气生产和供应业为规模收益递增产业，可以通过扩大规模来提高相对有效性，而其余产业为规模收益递减行业，不应盲目扩张规模，应该着重提高质量，提高相对有效性。

五、结论

第一，DEA/PCA 方法对于评价产业经济绩效是可行的，通过对中国工业产业的40 个行业进行排序，符合一定的客观事实，而且，通过符号检验法对两种排序结果进行差异显著性检验，证明两种结果无显著性差异。

第二，通过DEA/PCA 二维坐标屏幕，直观的分析了我国工业中40 个行业的相对有效性，只有4 个行业的相对有效性为优，是低投入高产出的高有效性产业，但是这4 个行业为石油和天然气开采业、酒、饮料和精制茶制造业、烟草制品业的传统行业以及废弃资源综合利用业，并没有高技术产业，证明我国高端制造业还有待发展。

第三，DEA 有效（θ=1）的行业共计有8 个，这些产业相对有效性最高，增加对这些产业的技术投资可以增加利润；其余规模收益递增的产业有10 个，可以扩大这些产业规模以提高效益，而对于剩余规模收益递减的产业，其发展重心应该在于提升质量方面[8-10]。