平台商业模式下基于Shapley值修正的中小物流企业联盟利益分配研究

孙 鹏，张冰玉

(湖南工商大学,湖南 长沙 410205)

一、引言

在“互联网+”环境下，随着企业商业模式的巨大变化，全球 TOP100 家企业里，60%的企业的营收主要依赖平台商业模式。平台商业模式下如何组建全新的物流企业联盟，通过协同合作使新兴联盟为物流企业带来更大的经济效益，成为经济新常态与供给侧改革背景下物流运作的一项极为重要的任务。中小物流企业作为我国物流产业的主体部分，目前具有“多、小、少、散、弱”的特点，它们的缺陷主要表现在：信息化程度低，技术力量薄弱，业务辐射范围小，运营效率低且成本高。因此，许多中小物流企业纷纷建立物流企业联盟，但联盟不是盲目建立的，不少物流企业联盟因发展中存在的种种问题而失败解体。联盟失败的原因是复杂多样的，而利益分配问题是一个关键影响因素，它关系到物流企业联盟能否稳定持续地运营。因此选取合理的利益分配策略，既是物流企业联盟稳定运营的基础，又是调动各成员积极性的有效助力。

近年来，联盟利益分配问题的研究引起国内外学者的关注，很多学者对物流联盟利益分配问题进行了研究[1-2]，国外学者主要运用夏普利(Shapley)值法、欧文(Owen)法、Selectope等方法进行定量研究,如Nadia Lehoux et(纳迪亚，2016)[3]等人通过调查分析，提出了企业建立联盟的必要性和重要性，并利用Shapley法对整个联盟的利益进行了分析。ShougengGu(2016)[4]针对甩挂运输的特点，采用 Shapley法建立了两阶段的效益分配模型。国内学者采用改进的 Shapley 值法、博弈论法、风险系数法等展开对利益分配的研究[5-10] [14],如王鹏、陈向东(2011)[11]用规模经济、技术先进及资金运作三个指标对物流企业联盟中各成员进行评价，从而对Shapley值进行改进，得到体现成员重要性的利益分配策略；于洪伟(2012)[12]、傅硕文(2015)[13]运用加权群体重心算法，综合Shapley值法、Nash均衡、MCRS法三种方法分别得到的利益，组成三维矩阵而最终得到利益分配策略；王现兵(2017)[15]基于TOPSIS法对中小物流企业联盟各成员的边际贡献、投入成本、努力水平和风险承担进行评估，建立多因素视角下的利益分配模型；杜志平等(2018)[16]采用 FAHP-Shapley 的利益分配模式，对影响其利益分配的多重因素进行综合量化分析，并构建出4PL 模式下跨国电商物流联盟利益分配的指标体系。由此可见，学术界对Shapley值的应用研究较多，并针对传统Shapley值法的不足进行了改进，但多数只考虑单一因素的影响，忽视了多因素综合影响对利益分配的调节作用，且对修正因素的剖析不够细致全面。因此，本文借鉴前人的研究成果，通过建立包含企业综合实力、投资额、风险量等因素对传统Shapley算法进行改进，并将其应用于中小物流企业联盟的利益分配问题。

二、中小物流企业联盟利益分配的影响因素分析

1.物流企业的综合实力

传统Shapley法是依据各个成员的边际贡献来分配利益的，它假定联盟中各成员在其余方面是完全平等的，但事实上尽管都是中小型的物流企业组成的联盟，各联盟成员的规模、发展潜力等企业综合实力不同，从而对于联盟的重要性程度也不同。综合实力强的物流企业更容易占据主导地位，在联盟的利益分配协商中讨价还价能力更强。这里所说的企业综合实力尤指对于物流企业联盟能产生实质性正向作用的企业竞争力。物流联盟的收入是从物流业务中获取，物流业务量也代表了一个物流企业的客户资源量以及物流服务的好坏，体现了企业的业务范围与业务能力，是物流企业综合实力关键的衡量指标之一。物流企业联盟物流任务分配的过程同时也是资源整合的过程，资源整合包括信息资源整合、客户资源整合、仓储设备与设施整合等。资源整合能够使得联盟效益最大化、成本最小化、服务质量最优化，对于物流联盟的运作有着举足轻重的作用。因此若一个企业资源整合能力越强，在物流企业联盟中就更能占据主导地位。根据外部规模经济理论，物流企业的集聚能够产生行业的技术与知识积累，知识技术外溢的结果是整个物流企业联盟技术协同进步。若一个物流企业的知识技术外溢度更高，说明该企业技术力量更雄厚、创新能力更强，对于整个联盟的技术升级起着带头作用。因此考虑到指标的简明性和实用性，本文采用三个指标对物流企业综合实力进行评价，分别是物流业务量、资源整合能力以及知识技术的外溢。

2.物流企业的投资额

物流企业联盟中各成员对于联盟的投资大体上分为两种，即有形投资与无形投资，有形投资指的是人员、车辆、各种设施设备、资金等方面的资源投入，而无形投资指的是企业声誉、风险对抗、信息、管理等方面的投入，无形投资包含了企业综合实力与风险分担的内容，这里所说的投资额指的是有形投资。根据投入与收益相对应的基本原则，物流企业在联盟中投资额越多，分得的利益也更多。

3.物流企业承担的风险量

在组建联盟后，物流企业所面临的风险不仅仅来自于其自身和市场环境，还来自联盟内部。主要有以下几种：由于缺乏沟通交流、信息不对称、契约不够完备导致的成员间合作不协调的风险；其他合作成员由于能力不足而失约的风险，这又包括了伙伴企业未按计划时间完成任务、任务完成不当引起的合理范围之外的货差和货损、技术不够成熟或对项目预测不足导致的困难等所造成的风险；管理不当如企业文化冲突、企业丧失自主地位对联盟和其他企业形成过度依赖等风险；企业核心技术及机密泄露的风险；合作伙伴单方违约或造假行为导致的信用风险等。物流企业联盟中的风险是多而复杂的，每个成员所承担的风险也不可能等同。高风险对应高收益，这意味着在联盟中承担风险更多的企业分配到的利益也更多。

三、基于Shapley改进的利益分配模型构建

(一)基本Shapley模型

Φi(v)=

(1)

(2)

其中|s|是子集s中元素的个数，n为集合I的元素个数,v(s-i)表示联盟中除去i企业后所能获得的收益，当联盟中i企业加入某个联盟集合S中时，联盟集合S增加的收益为v(s)-v(s-i)。

式(1)中的W(|s|)表示物流联盟集合S的加权权重，它的数值与具体某一企业无关，而是根据联盟中全部企业的个数n与集合S中企业的个数|s|来确定。

现构建一个拥有三个物流企业A,B和C的物流企业联盟，A、B和C三个企业独自运营时利润额分别是a1、a2、a3，当企业A与企业B组成联盟进行合作时预计利益额为b1，当企业A与企业C组成联盟时预计利益额为b2，企业B与企业C组成联盟时预计利益额为b3，当A、B以及C三个企业共同组成联盟进行合作时，预计可得c的利益额。

记I={A,B,C}，企业A与企业B组成的子联盟记为A+B，企业A与企业C组成的子联盟记为A+C，企业B与企业C组成的子联盟记为B+C，三个企业一起组成联盟记为A+B+C。由于此时n=3，可计算得到W(|s|)的值，当|s|=1时，即联盟集合中只有一个企业时，W(|s|)=1/3,同样地|s|=2时W(|s|)=1/6，|s|=3时W(|s|)=1/3。

根据式1用夏普利值法求得A、B、C三个物流企业组建联盟后各自所分配到的利益，记做φA(v)，φB(v)，φC(v)。计算得A企业、B企业在联盟中所分得的利益为：

计算得C企业在联盟中所分得的利益为：

(二) Shapley的改进

结合以上物流企业联盟利益分配的影响因素以及联盟利益分配的原则，在基于夏普利值法的基础上，对联盟的利益分配机制进行改进。

1.考虑物流企业联盟中各成员的综合实力

在n个企业组成的联盟中，考虑到各成员企业的综合实力的利益分配的变化变量为：

△φpi(v)=φ(v)×(αi-1/n)

(3)

其中φ(v)为物流企业联盟的总利益，αi为该企业的综合实力相对于整个联盟的权重。∑(αi-1/n)=0,αi-1/n表示物流企业联盟中企业的综合实力与理想情况(即各成员无差异)下的差值，当该值大于0时，表示该成员企业综合实力更强，对于物流企业联盟更为重要，在联盟各企业进行利益分配协商时讨价还价能力更强，因此可分得更多的利益。

仍以A、B和C三个物流企业来做说明，A、B、C三个企业以其企业综合实力所体现的在联盟中的重要性权重分别为αA，αB和αC，用层次分析法来计算各企业权重的大小。根据层次分析法的操作步骤，首先要建立层次结构模型：目标层为对物流企业联盟中各企业综合实力评价，求得αA，αB和αC； 在企业A、B、C组成联盟的模型中，n为3，可求得各自的利益分配变量分别为：

△φpA(v)=c×(αA-1/3)

△φpB(v)=c×(αB-1/3)

△φpC(v)=c×(αC-1/3)

2.考虑物流企业联盟中各成员的投资额

假设企业i的所有投资额为Ii，联盟中n个企业的投资额大小向量为I={I1,I2,…，In}，仅考虑投资额这一影响因素，不考虑其他的因素时，物流企业联盟中各企业的利益变量为：

(4)

对于A、B、C三个企业来说，根据投资额因素其各自在物流企业联盟中的利益变量为：

3.考虑物流企业联盟中各成员承担的风险量

基本的Shapley模型中假定联盟及子联盟中各企业合作成功的概率为1，但是实际上本非如此，因此在原本的Shapley模型中引入风险因子对其进行改进能更贴合实际。在n个物流企业组成的联盟中，基于风险这一因素的各个物流企业的利益变量为：

(5)

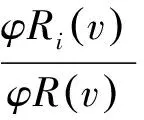
在上述物流企业A、B以及C三者组成的联盟中，企业A、B和C各自独立运营时成功概率为1，假定企业A与企业B进行合作组成联盟成功的概率是为R1，企业A与企业C组成的联盟成功的概率为R2，企业B与企业C组成的联盟成功概率为R3，三个企业共同组成的联盟成功的概率为R4。

那么此时物流企业A所分配到的利益为：

φRA(v)=

物流企业B所分配到的利益为：

φRB(v)=

物流企业C所分配到的利益为：

φRC(v)=

φR(v)=φRA(v)+φRB(v)+φRA(v)

(三)综合三种影响因素的Shapley改进模型

单独考虑企业综合实力、投资额和风险量任何一个因素对利益分配结果进行改进都是较为片面的，为了使得物流企业联盟利益分配的结果更加公平合理，应当将这三种影响因素按其重要性程度与原来的夏普利值法模型进行融合。这三个因素的相对权重可以通过德尔菲法或者层次分析法来求得，记企业综合实力的相对权重为w1，投资额权重为w2，风险量的权重为w3。则改进的夏普利值法模型中，各个成员企业可获得的利益为：

φi(v),=φi(v)+w1×△φpi(v)+w2×△φIi(v)+w3×△φRi(v)

(6)

将A、B、C三个物流企业的原始利益值与基于各因素的利益变量值代入改进的Shapley公式，即公式6中，就可得到经过调整修正之后各企业最终所得到的利益，从而得到物流企业联盟中改进后的利益分配比例。

四、算例分析

假设三个物流企业A、B以及C共同组建物流企业联盟。企业A、B和C在2018年独自运营所获得的利润分别为130万元,120万元,100万元，当企业A同企业B进行合作时可获得利润300万元，企业A和企业C组成的子联盟预计可获得260万元，企业B与企业C组成的子联盟预计可获得240万元。三个物流企业组成联盟进行合作，预计整个联盟利润额为420万元。通过层次分析法得到三个企业的综合实力权重。准则层权重计算如表1所示，各企业物流业务量、资源整合能力、技术知识外溢三个指标的权重计算如下：

表1各物流企业综合实力权重计算表

所以αA=0.403，αB=0.363，αC=0.234

对于物流企业联盟，A企业初始投资额为180万元，B企业初始投资额为200万元，C企业初始投资额为220万元。

A、B、C三个企业独立运营成功的概率为1，A与B的联盟成功概率为0.9，A与C联盟成功概率为0.85，B与C联盟成功概率为0.9，如果三家企业共同组建物流企业联盟，则成功的概率是0.8。

企业综合实力、投资额、风险量的相对权重分别是0.27,0.61,0.12。

表2算例数据与模型参数对照表

首先求得各个影响因素导致的各企业利益变化量，再与初始利益值进行加总，得到修正后的利益分配值。

表3 赋权后各利益变化量计算数据以及两模型结果比较 万元

从表2、表3数据分析可以看出，在各物流企业中，A企业的企业综合实力最强，尤其是其物流业务量大，能够给整个联盟带来更多的客户资源从而带来更多收益，因此A企业在物流企业联盟利益分配协商中有更强的讨价还价能力，多分得7.9万元的利益。B企业次之，多分得3.36万元，而C企业由于综合实力不足，要给出11.26万元来补偿其他成员。在投资额这一方面，C企业投入最多，因此要得到8.54万元的投入补偿。B企业投资额恰好是联盟整体投资额的三分之一，因此无功无过。而A企业投资额最少，因此要扣除8.54万元来补偿C企业。就各企业承担的联盟风险而言，C企业承担风险最小，相应地其收益要扣除2.99万元，来补偿承担风险量最大的A企业和风险量较大的B企业，由两企业按比例分摊。从三个物流企业的收益变化角度分析，改进后A企业由于其综合实力最强且承担风险量最大，尽管其投资额最小，仍多分得1.66万元；B企业在综合实力、投资额以及风险承担各方面都居第二，其最终收益增加了4.05万元而C企业虽投资额最多，但其综合实力最弱，承担风险也最少，所以最后总收益减少了5.71万元。

这个算例验证了改进的Shapley模型的可行性，同时也说明了在企业实力更相近的联盟中，利益分配才会更平均，而企业实力相差越悬殊，利益所得相差也会越大，因此企业在加入联盟并进行投资的同时，也要注重企业自身综合实力的提升。此外，对于企业抵抗风险的能力也要引起重视，要加强对于风险事故的防范，这一因素也会造成利益分配额的变动。

五、结论

在平台商业模式下，中小物流企业联盟日益频繁，合理的利益分配机制是联盟发展的重要保障。本研究基于多因素视角引入企业综合实力、投资额以及风险承担量三个利益分配影响因素；将三个影响因子赋予权重并与Shapley模型结合，得到综合考虑多因素的Shapley值改进模型，结果显示改进后的利益分配模型使得联盟中各成员的利益分配结果与初始Shapley值模型相比发生了部分合理变动，更加体现公平性，也更贴近实际。