汽车总装线配置问题的数学模型
2019-11-22陈卫忠
陈卫忠
(苏州市职业大学 数理部,江苏 苏州 215104)
1 问题的提出
某汽车公司生产多种型号的汽车,每种型号由品牌、配置、动力、驱动、颜色5种属性确定。品牌分为A1和A2,配置分为B1、B2、B3、B4、B5和B6,动力分为汽油和柴油,驱动分为两驱和四驱,颜色分为黑、白、蓝、黄、红、银、棕、灰、金。公司每天生产各种型号车辆的具体数量,根据市场需求和销售情况确定[1]。
本文参照2018高教社杯全国大学生数学建模竞赛D题。题目中给出的装配要求为:装配当天两种品牌各一半数量的汽车,相同驱动、动力连续装配数量不得超过2辆,两批汽车之间间隔数量至少是10辆,同种颜色的汽车应尽量连续喷涂作业,不同颜色汽车之间的切换次数尽可能少,总装线和喷涂线的各项要求对相邻班次的车辆同样适用。根据装配要求提出下列问题:参照问题的背景、装配要求,建立数学模型,得出符合要求且生产成本较低的装配顺序[1]。
2 问题的分析和模型假设
对于汽车总装线的配置问题,要在尽可能地满足装配要求的情况下求得具有较低生产成本的装配顺序。由于每种型号汽车有品牌、配置、动力、驱动、颜色5种属性,且颜色有9种,不同颜色汽车的搭配和间隔比较复杂,因此,采取手动排列且假定黑色可与任意的颜色间隔排列;由于品牌的装置顺序是固定的先A1后A2,因此,分别对A1和A2进行装配顺序的建模,且假定同一品牌下相同配置车辆尽量连续;对于配置、动力、驱动属性,假定动力、驱动属性中的两批间切换次数越少,则间隔数量满足大于10辆的可能性就越大,因此,首先以不同属性中的两批间切换次数为目标建立0-1规划模型,然后确定品牌和喷涂线顺序,最后手动排列颜色装配顺序[2],从而得到符合要求且生产成本较低的装配顺序。
3 模型的建立和求解
驱动属性分为两驱和四驱,要求四驱汽车连续装配数量不得超过2辆,两批四驱汽车之间间隔的两驱汽车数量至少是10辆;动力属性分为汽油和柴油,柴油汽车连续装配数量不得超过2辆,两批柴油汽车之间间隔的汽油汽车数量至少是10辆;配置属性分为B1、B2、B3、B4、B5和B6,同一品牌下相同配置车辆尽量连续,减少不同配置车辆之间的切换次数。为此,在不考虑品牌和颜色属性的前提下,以剩余属性中的两批间切换次数为目标,建立规划模型[3]。

利用Lingo软件对模型进行求解,得出某品牌某一天的配置、动力和驱动的装配顺序。由于品牌的装配顺序是固定的先A1后A2,在同一品牌下相同配置车辆尽量连续装配的前提下,按照A1→A2→A3→A4的品牌装配顺序,利用Lingo软件求解0-1规划模型得到配置、动力和驱动的装配顺序并进行整合。
对于颜色属性,由于颜色有9种,喷涂线两条C1和C2,汽车总装线上排列为单数序号的汽车在C1线上进行喷涂,双数序号的在C2线上进行喷涂,且不同颜色汽车的搭配和间隔较复杂。蓝色、黄色、红色只在C1线上喷涂,金色在C2线上喷涂,其他颜色在任意一条线上喷涂;同一喷涂线上,同种颜色尽量连续喷涂,且不同颜色汽车之间的切换次数尽可能少,黑色汽车连续排列在50~70辆,两批黑色汽车至少间隔20辆;蓝色必须与白色间隔排列,黄色或红色必须与银色、灰色、棕色、金色中的一种间隔排列,灰色或银色必须与黄色、红色、金色中的一种间隔排列,棕色可以连续排列,也可以与黄色、红色、金色、白色中的一种间隔排列。
首先考虑特殊的颜色,即可能搭配颜色数量较少和限制要求较多的颜色,见表1。

表1 可能搭配颜色与喷涂线
由表1可知,蓝色的可搭配颜色只有白色,且被限定在一条喷涂线C1上,所以蓝色是特殊颜色。首先排蓝色,接下来考虑汽车生产数量较多的颜色黑色与白色,最后考虑颜色间隔情况。黑色汽车要求两批之间有间隔且至少2辆,这就需要选择能间隔黑色,并可搭配颜色数量较多的颜色。可搭配颜色数量多的颜色有黄、红、银、棕、灰、金6种,则在这6种颜色之间,再按照可能搭配颜色数量较少和限制要求较多的颜色先排的原则进行排序。手动排序逻辑图,如图1所示。
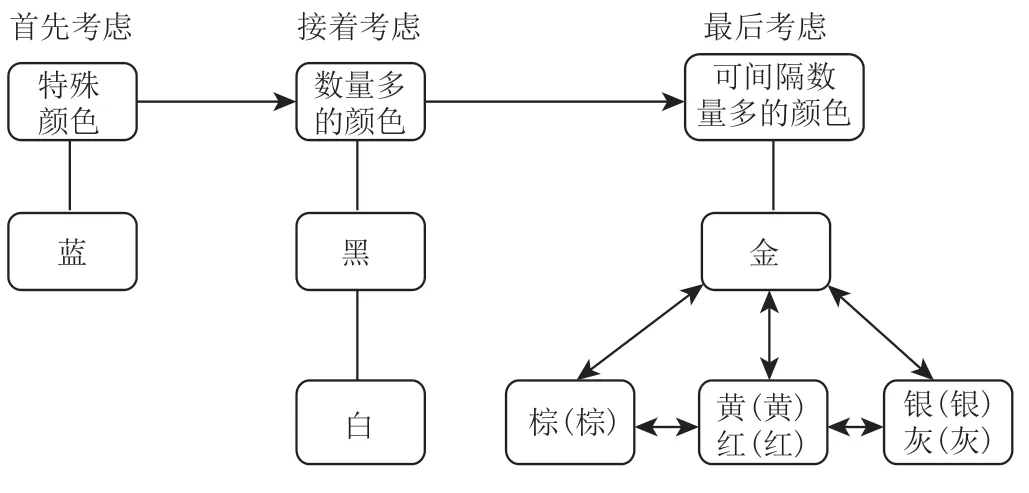
图1 手动排序逻辑图
4 结论
为了提高汽车生产效率,实现多种车型共线生产,汽车总装线的配置顺序尤其重要。鉴于汽车型号由品牌、配置、动力、驱动、颜色5种属性确定,导致多种车型共线生产的总装线的配置顺序极其复杂。本研究在满足装配要求的情况下,首先固定品牌配置顺序,建立配置、动力、驱动切换次数最少的0-1规划模型,最后手动配置装配顺序,求得具有较低生产成本的汽车总装线的配置顺序,提高汽车生产效率,节约汽车生产资源,且有实际的应用意义。
