数值分析实验课教学模式探讨

张伟红

（合肥师范学院数学与统计学院，安徽合肥230601）

关键字：数值分析；数学实验教学模式；分层递进教学；Matlab

数值分析是研究各种数学问题求解的数值计算方法。它的特点是理论和实践相结合，既重视各种模型方法的理论分析，又重视这些方法的使用[1]。数值分析中模型的算法所面向的对象是计算机，所以在教学过程中数值实现必不可少。Matlab是一个集数值计算、符号分析、图形可视化、文字处理于一体的大型集成化软件，已经成为神经网络、最优化、计算机及电子信息等方面的教学或科研的常用工具。它的特点是语法简单，易于学习。数值分析实验课选用Matlab软件平台进行教学，编程容易上手，有助于学生把重点放在算法的实现上，且Matlab具有强大的数值计算功能，使用起来非常方便，可以省去一些不必要的编程，便于学生比较和验证计算结果。

在数值分析教学过程中，学生对算法的理论学习容易掌握，但解决实际问题的能力欠佳，而这种学以致用的能力往往在就业过程中是公司或企业更看中的。所以在课程的讲授过程中，希望能结合课程特点注重培养学生的实践应用能力和创新能力，从而提高学生的综合能力，让其更好地步入社会，适应社会需求[2]。但传统实验教学方式不能有效地发挥培养学生应用能力的作用，常见问题有实验教学中内容单一、只是验证性实验、学生学习主动性不高、相互抄袭实验报告；单一的教师给实验内容、学生做实验、提交实验报告的教学模式，不便于掌控课堂，不易调动学生的学习积极性，不能很好根据实验过程和实验结果评判实验成绩。因此国内诸多的教学工作者一直在探索数值分析实验教学方式[3-5]，以更好地引导学生让其学会思考、探索、改正，且在这个过程中培养他们应用数学知识、分析问题并选择适当的算法编写计算机程序来解决实际问题的能力。

为了避免传统教学中的问题，教学过程中需要注意：1）学生是学习的主体，教师起引导作用；2）分解实验任务，明确实验要求，给定时间结点，完成相应任务；3）展示学生实验成果，激发学生学习热情。根据这些注意事项，结合实验教学经验，为提高学生学习积极性、培养学生分析、解决问题能力，提出一种新的适合应用型本科院校数学与应用数学专业学生的实验教学模式。

1 “分析-实践-演示-完善-进阶”式实验教学模式

“分析-实践-演示-完善-进阶”式实验教学模式，是一种分层递进的教学方式，本质上是将实验内容分解成基础实验和提高实验两部分。基础实验部分是对算法做验证性实验，提高实验部分是在验证性实验完成的基础上进一步提出更高要求的实验，如改进算法或利用基础实验结果去求解其他问题等等。其中“分析”是教师在学生实验前先将实验内容进行讲解、分析，引导学生思考如何将算法转化成为程序，并给出实验内容的流程图；“实践”是让学生基于分析结果进行基础部分的实验，结合流程图利用数学软件写出算法的程序，并利用程序做简单的计算；“演示”是教师在学生做了基础实验之后，现场演示个别条理性比较好的学生的实验结果，并对照流程图进行讲解和说明；“完善”是在教师演示过基础实验的程序之后，给学生时间去修改和完善自己的程序；“进阶”是在基础实验的基础上给出更高要求的实验内容，让学生思考基础实验的本质并改进或利用它，这部分实验让学生自己独立完成。

“分析-实践-演示-完善-进阶”式实验教学模式，在实施过程中要注意控制实验时间，基本上按照“10-25-10-15-30分钟”时间分布来执行。同时注意控制课堂秩序，学生可以相互讨论的实验阶段是“实践”和“完善”阶段，“进阶”部分独立完成、不能相互讨论。实验报告是实验内容的总结阶段，要求学生能将实验过程中所得出的实验结果进行分析、改进，并总结进而写出实验报告和心得体会。这种分层递进的实验过程，教会了学生如何将所学理论转化成程序并使用，有效地培养了学生分析问题、解决问题的能力和编写程序处理问题的能力。

2 实验案例

实验的目的是让学生掌握拉格朗日插值方法，然后将其转化成程序，并利用所写程序构造高次和低次的插值曲线。进一步让学生感受高次插值带来的龙格现象，以及学习解决龙格现象的分段低次插值方法。结合上面所提出的实验教学模式，对于这次实验课，具体的实验过程如下。

1）“分析”阶段

首先教师带着学生复习拉格朗日方法，写出拉格朗日插值公式，并让学生明白公式中已知量是什么，待求量是什么，即让学生清楚程序的输入量和输出量，

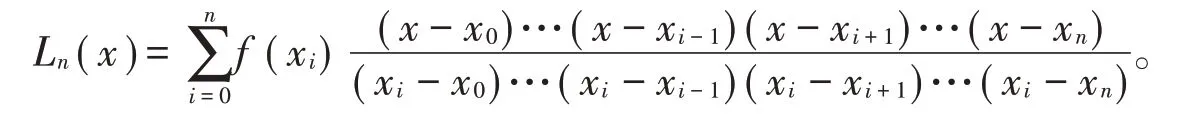
然后要求学生根据拉格朗日插值公式，封装一个Mylagrange（输入量）的函数，后面绘制插值曲线可以直接调用Mylagrange函数。为了避免学生从网上直接拷贝拉格朗日的程序来交差，教师需要带着学生进一步分析拉格朗日函数的内涵，将问题继续分解。引导学生观察拉格朗日的表示形式：基函数的线性组合，并带着学生依据数学公式写出拉格朗日函数的流程图，指出输入量和输出量，说明这个流程图的主要结构是一个循环结构，对应Matlab语言就是for循环。提示学生将基函数先封装成一个函数LagBase（节点信息），然后在一个循环语句里调用这个函数给出拉格朗日函数Mylagrange。为了便于学生写出基函数的程序LagBase（节点信息），对基函数的形式进行简化：

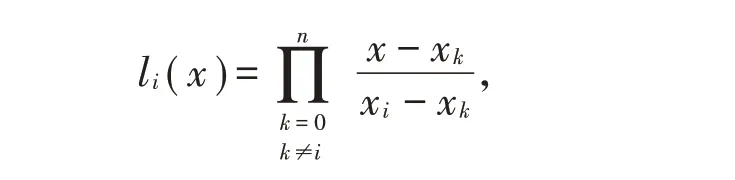
结合该形式给出基函数的流程图，并引导学生思考基函数的程序。

2）“实践”阶段

这个阶段就是留给学生去实践，让他们去消化“分析”阶段的结果，实现自己的想法。教师鼓励学生自己动手去做实验，及时帮助他们发现并克服编程中遇到语法等程序问题。同时要善于观察并发现这些程序写得好的学生，在下一阶段中演示这些学生的程序。

3）“演示”阶段

演示个别学生的结果，并对照“分析”阶段中的流程图进行逐句讲解，教会学生怎样根据流程图写程序。将基函数的程序单独列出来，并结合例子验证程序的正确性，再结合拉格朗日函数的流程图，对照讲解拉格朗日函数的程序。

4）“完善”阶段

经过上面的3个阶段，学生已经在教师的讲解下清楚写程序的整个过程。这个阶段就留给学生，让他们自己反思自己程序中的问题并结合上面的演示过程进行修改。

5）“进阶”阶段

这个阶段是让学生学习使用自己的程序去处理一些简单的问题。让学生从中获取学习这些方法的乐趣，同时进一步让学生去思考现有方法中存在的问题。这个阶段所包含的信息量较大，便于教师通过这个环节掌握学生的真实学习情况。这次实验课的“进阶”阶段，包含3部分内容：

（a）利用拉格朗日函数程序，绘制出给定函数f (x)的10次插值曲线；

（b）利用拉格朗日函数程序，绘制出给定函数f (x)的4次插值曲线；

（c）利用拉格朗日函数程序，将定义区间分两段，分别在每段上构造相应的4次插值曲线，并绘制出插值曲线图。

题目（a）的设置是为了让学生观察高次插值的震荡现象，题目（b）的设置是为了让学生观察低次插值和高次插值的区别，题目（c）的设置是为了让学生体会如何利用现有办法去解决高次插值所带来的弊端。三部分内容都不难，但是对于没有理解拉格朗日函数程序的学生，就不知道如何下手；对于部分不会使用数学软件绘图的学生，也不能绘制出插值曲线。其实3个题目，实际操作本质上是一个过程，对上课专心听课且认真参与每个实验环节的学生，能很快完成。为了避免出现抄袭现象，这一阶段的完成过程，要求学生可以翻阅资料，但是不能左顾右盼，且对大家的要求是（a）、（b）是需要大家完成的部分，做完（a）和（b）就可以写实验报告，并提交实验报告。（c）能做完就补充进实验报告，做不完可以课后自己补充完成。这样可以结合课内实验报告完成情况和课后补充情况，给出符合实际掌握情况的实验过程分数。

3 结束语

数值分析是研究各种数学模型的数值计算方法，它面向的对象是计算机。这就决定了数值分析课不能像其他数学课一样，只注重理论。不经过数值实验学生就不能深刻理解数值分析的本质。文中所提出的这种“分析-实践-演示-完善-进阶”式实验教学模式，是在长期教学过程中总结出来的，是一种分层递进的教学过程，有助于激发学生的学习兴趣，提高学生动手能力，提高课堂教学效果。但仍有有待改进的地方，在今后的教学中还需不断完善。