基于Excel数据建模求解及结果分析
2019-11-21石建国
石建国
(安徽工程大学计算机与信息学院,安徽芜湖241000)
数据分析和处理在各领域都有重要的应用,根据数据之间的关系和实际问题的需求,建立现实问题的数学模型,通过相关软件或设计算法并进行编程对模型进行分析和求解,以此找出解决问题的最优化方案。为此,需要借助数据处理软件进行复杂数据的处理,常用的数据处理分析软件有Excel、SPSS、Matlab、R等。但除Excel外,其他软件对数据分析人员的专业技术能力要求相对较高、使用较复杂、软件购置费较昂贵,成为使用过程中的一个瓶颈。
规划求解问题在很多领域都有广泛的应用,如果不用Excel求解,通过编程实现非常复杂,而且算法的准确性不易得到保证。类似的数据处理工具诸如Spss,虽然也具有较强的数据处理和分析功能,但与办公软件如Office或WPS兼容困难;另一种用于数值分析和计算的重要软件Matlab虽然功能强大,但较难掌握,尤其是在算法设计和实现时需要通过对象化编程,程序执行速度较慢,而且使用成本昂贵。Excel是一款通用且简单易学的数据处理软件,同时具有操作简单方便、使用广泛和成本低等优点,常用于一些简单的数据处理。同时,Excel也有一些实用功能可解决复杂的应用问题,但这种复杂的应用在普通教材和Excel帮助中均没有详细介绍。文章通过实例探讨利用Excel规划求解工具求解最优化问题的思路和方法,并对处理结果中输出的敏感性报告进行了分析,并验证了结论的正确性。
1 Excel数据处理及分析方法
(1)Excel提供了很多数据处理和分析方法。目前常见的应用于数据处理的方法有排序、筛选、分类汇总、合并计算及各类数据处理函数,这些数据处理方法,通过简单学习便可熟练掌握并运用。
(2)用于数据分析的方法有规划求解、数据透视图表、各类图表(如条形图、柱形图、散点图、饼图等)、描述性统计、均值推断、概率统计、回归分析(线性回归、逻辑回归和多元回归等)、时间序列、T-test、Z-test等。其中描述性统计和概率统计方法通常用于汇总数据,其与回归分析、T-test和Z-test统称为传统的统计分析方法。时间序列用于预测分析,为非传统统计分析方法[1]。
2 线性规划问题求解
线性规划问题数学模型通常由变量、约束条件和目标函数3个要素组成。通过列出约束条件及目标函数,找出约束条件所表示的可行域,在可行域内求目标函数的最优解[2]。根据现实情况,从中建立数学模型一般分3个步骤:(1)根据目标影响因素确定决策变量;(2)由决策变量和目标之间的数量关系确定目标函数;(3)根据决策变量的客观限制条件确定决策变量应满足的约束[3]。以下以运输问题为例来阐明Excel在线性规划求解中的应用。
3家企业X1、X2、X3生产同一产品,其产量分别是46、22、32(单位:万件),现要将产品运到Y1、Y2、Y3、Y44个地方,这4地的产品需求分别为27、39、20和14(单位:万件),试确定最优化方案[4]。从产地到销地的产品运价如下面矩阵所示:
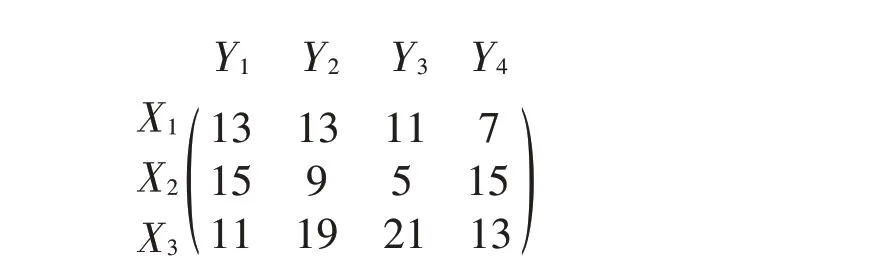
若设xij为从产地Xi到需求地Yj的产品运输量,则该运输问题的线性规划模型为
min Z =13x11+13x12+11x13+7x14+15x21+9x22+5x23+15x24+11x31+19x32+21x33+13x34,将上述模型对应的数据填入Excel工作表中,如图1所示。各单元格之间的运算关系如表1所示。

在Excel 中点击“数据”菜单,找到“模拟分析”中的“规划求解”选项,出现图2“规划求解参数”对话框。其中求解目标在工作表的B14单元格显示,数据可动态改变的单元格范围为$B$8:$E$10,满足的约束条件为(1)$B$11:$E$11=$B$13:$E$13;(2)$F$8:$F$10 =$H$8:$H$10。

图1 运输问题的电子表格模型

表1 运输问题模型中的公式设置
点击图2中的“求解”按钮,在Excel中输出的最优解如图3所示。由图3可知,通过单纯线性规划得出的最优化运输方案为从X1调运32(万件)到需求地Y2,调运14(万件)到需求地Y4;从X2调运2(万件)到需求地Y2,20(万件)到需求地Y3;从X3调运27(万件)到需求地Y1,调运5(万件)到需求地Y2。这样可以使得运输费用最小为1 024(百元)。

图2 运输问题的规划求解参数设置
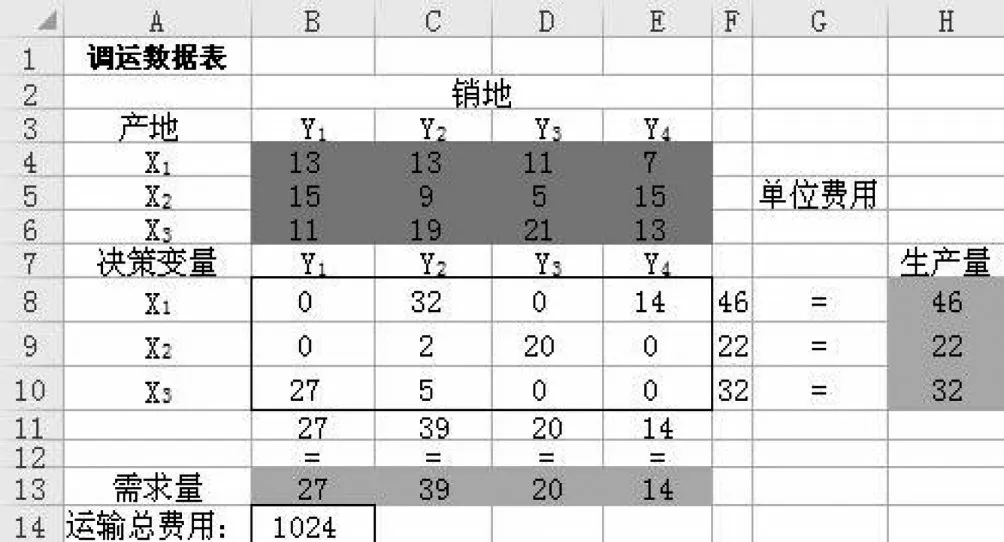
图3 运输问题最优方案
3 结果分析
结果分析中最重要的是敏感性报告中各项参数的分析,最重要的参数有阴影价格、递减成本、目标式系数和允许的增减量分析。
3.1 敏感性分析的内涵及作用
所谓敏感度分析,是指对某些可能变化的因素及其对决策目标影响程度的反复分析,以揭示决策方案如何随可变因素变化而变化[5]。实例中建立线性规划模型所需的数据都是已知的,这些数据被称为模型参数。但在现实应用中获取这些模型参数并不容易,需要付出大量时间和精力,并通过实践和检验才能获得可靠的数据,有时即使投入大量时间和精力,也只能得到模型参数的粗略估计或预测值。因此,结果分析需要研究两个问题:一是当参数中的一个或多个发生变化时,已求得的线性规划最优解会如何变化;二是参数在什么范围内变动,最优解能够保持不变[6]。
敏感度分析的作用主要有两点:(1)可了解相关因素的变动对决策方案、目标或者其他评价指标的影响程度,找到影响最优决策方案的相关因素,并进一步分析或者估算影响决策目标的不确定因素,有利于比较不同备选方案对关键敏感因素的影响程度,以便选择敏感性相对较小的方案,从而减小决策风险。(2)帮助决策者掌握方案最优与最劣的可能变动范围,通过分析把握如何采取有效控制措施,以便选取最有经济意义的决策方案[7]。
3.2 敏感性报告输出
在求解输出最优化运输方案时,点击“规划求解参数”界面的“求解”按钮,显示界面如图4所示。
选中“报告”框中的“敏感性报告”,点击“确定”,便可输出“敏感性报告”,对敏感性报告中的数据进行整理,输出结果如表2和表3所示。表2为可变单元格部分,对应于目标函数中的xij;表3为约束部分,即限制条件,对应于各地产销量的约束限制范围。

图4 规划求解结果界面
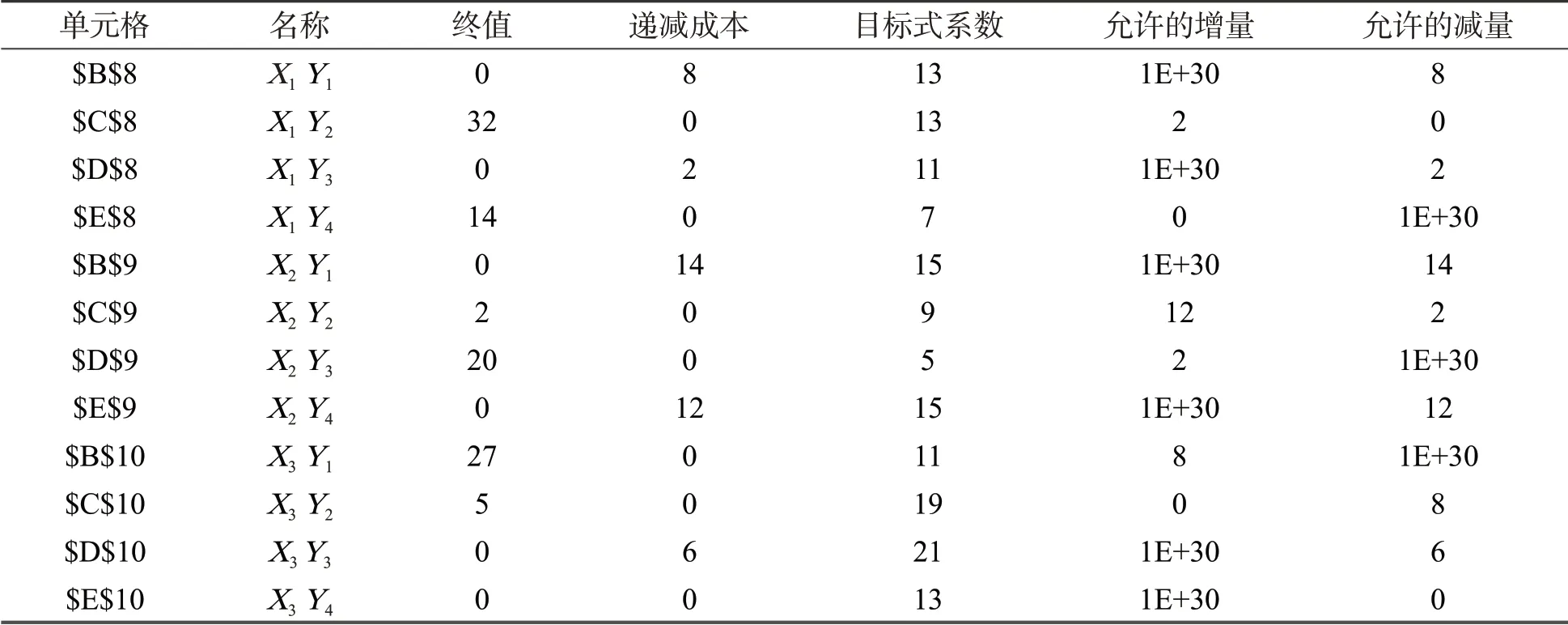
表2 敏感性报告之一:可变单元格部分
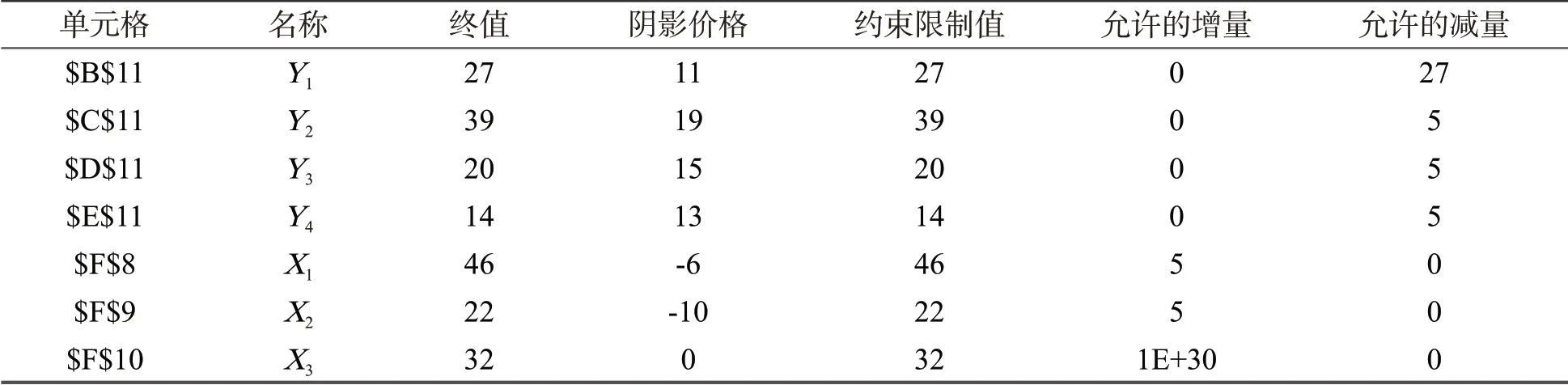
表3 敏感性报告之二:约束部分
3.3 参数分析
(1)可变单元格参数分析。可变单元格部分共提供5栏数据。“终值”表明问题的最优解,“递减成本”说明降低成本的数量,“目标式系数”表示单位运价,“允许的增量”和“允许的减量”标明单位运价在“已知运价,允许增量,允许减量”之间变动,运输方案可以不变。若超过这个范围,运输方案则需要变更。此范围即为最优解的敏感度。表中“1E+30”表示无穷大,此处可以理解为大于零的任意值。若设单位运价为xij,则在本例中,的变化范围为,则,即产地X1到销地Y1的单位运价x11的取值范围为。同理可得在保证运输方案不变的前提下,各产地和销地之间的单位运价xij的变动范围,结果如表4所示。

表4 单位运价变动范围
递减成本(Reduced cost)也叫减少成本,等于相应目标函数中变量检验数的值[8],是敏感性报告中的一个重要参数,是Excel输出时目标函数中xij的系数。而对于求最大值的线性规划而言,所有检验数必小于等于0;对于求最小值的线性规划而言,所有检验数必大于等于0。与之对应,如果目标函数若是求最大值,则递减成本必小于等于0。故根据递减成本的正负就能判断出目标函数是求最大值还是最小值。本例中目标函数是求最小运输费用,则递减成本必小于等于0。
同时,观察表2 中的终值和递减成本的对应关系,可以得出终值与其相应的递减成本的积为0,即×Rij=0(表示变量xij的终值,Rij表示变量xij的递减成本)。这种性质称为最优解与递减成本的互补松弛性[9]。据此,只要知道终值和递减成本其中一项不为0,则可推知另一项必为0。
表2中产地和销地之间没有产品运输关系的有6个。以X3→Y3为例,X3到Y3的单位运价为21(目标函数中x33的系数),如果要使X3Y3的终值不为零,即最优方案中有产地X3往销地Y3的产品运输,在保证最优解不变的前提下,可对表3中的R33参数进行调整,当R33的值由6减少到0时,才会出现X3Y3对应的终值不为0的结果。若其他条件不变,实例中产地X3到销地Y3的单位运价减少到15时,从产地X3才会运送产品到Y3,这就是Excel敏感性报告中递减成本蕴含的有价信息。
为验证上述判断的正确性,将产地X3到销地Y3的单位运价改为15,运用非线性内点法重新求解一次,得到的最优解如表5所示。
由表5可知,方案更改后产地X3到销地Y3有2万件产品的运输量(对应于灰色单元格数值)。将表5数据代入目标函数,与之前的最优运费相同,验毕。

表5 单位运价变动后的最优化方案
(2)约束部分参数分析。约束部分最重要的参数是阴影价格,通常也称影子价格。影子价格是指线性规划模型中某个约束的右端常数项增加(或减少)一个单位而导致的目标函数值的增量(或减量)[10]。影子价格客观地反映了资源在系统内的稀缺程度,影子价格越高,这种资源越稀缺。而影子价格为零的约束资源为富余资源。由阴影价格的定义可得出,阴影价格反映的是单位资源(消耗)的价值(费用)。
第一个约束销地Y1的影子价格是11,说明销地Y1每增加1个需求量,目标函数运输总费用会增加11个单位。也就是说,目标函数的最优解会发生变化,从“允许的增量”一栏中可以看出,实例中销地Y2的阴影价格最大,说明Y2每增加1个需求量所增加的运输总费用最高。但从表3可以看出,销地Y1、Y2、Y3和Y4“允许的增量”为0,产地X1、X2和X3“允许的减量”也为0,说明销地增加需求量和产地减少生产量都将导致最优解发生改变。
现在假设如果市场条件已发生变化,生产量和需求量需要同时增加(或减少),仍然保持产销平衡状态。当生产和需求同时增加时,X1和X2允许的增量都为5(万件),X3允许的增量为任意值,假设总的需求量增加5(万件),生产量也要同时增加5(万件),这时仍满足产量和销量相等。运用Excel进行进一步求解分析,目标是当生产量和需求量各增加5(万件),保持产销平衡,得出运输总费用增加最少的最优化方案,所得结果数据如表6所示。

表6 运输总费用增量表
从表6可以看出,在X2生产量增加5(万件)和Y1需求量增加5(万件)的情况下运输总费用增加最少,这是因为在表3中,产地X1的阴影价格为-6,X2对应的阴影价格为-10,X3的阴影价格为0,说明X2增加产量比X1和X3对总费用的降低最大。同时,销地Y1对应的阴影价格为11,Y2对应的阴影价格为19,Y3对应的阴影价格为15,Y4对应的阴影价格为13,说明Y1增加需求量比Y2、Y3和Y4对总费用的增加最小。因此,在生产量和需求量都同样增加保持产销平衡的情况下,在产地X2处生产最划算。同理,在生产量和需求量都同样减少保持产销平衡的情况下,不难判断在X3处减少生产最合理。
4 结束语
Excel在数据处理和分析方面还有很多重要应用,比如通过统计分析对大量数据进行统计处理;通过回归分析找到数据内在规律,并可用于预测和控制等问题;通过时间序列分析进行市场预测以及制定生产计划等。但最重要的是要理解数据背后所表达的现实含义。文章以线性规划中的运输问题为例,通过对数据处理结果进行分析,揭示敏感性报告中的重要参数的现实内涵,通过验证证明了结论的正确性,对于使用Excel进行数据处理和分析的人员具有一定的参考价值。
