自研激光雷达三维点云配准技术
2019-11-21呼延嘉玥徐立军李小路
呼延嘉玥,徐立军,李小路
(北京航空航天大学 仪器科学与光电工程学院,北京100083)
近年来,激光雷达三维扫描技术发展迅速,是获取空间三维信息最重要的方法之一。因为其便捷快速、测量范围广、精度高的特点,被广泛应用于数字城市、地形测绘、文物保护、自然灾害监测等领域[1-2]。传统获取物体表面三维信息的方法,主要包括基于激光雷达的三维扫描方法[3]和基于图像的三维重建方法[4]。
基于TOF(Time of Flight)三维扫描激光雷达,计算光的飞行时间获取距离信息,可以解算物体的空间三维坐标。这种方法测距精度高、工作距离远、操作简单,但无法为重建场景提供纹理信息,且存在位置限制和遮挡等问题,通常难以获取完整表面[5]。基于图像数据三维重建方法,获取某一物体多视角下的图像,利用三角测量原理计算图像像素间视差,从而解算物体的三维几何信息。这种方法虽然能够获取丰富的纹理信息,但重建点数量少且精度低,当图像质量不佳时,重建效果较差[6]。激光雷达与图像相结合的三维重建方法兼具两者优势,因此受到国内外学者关注,已在纹理映射、导航定位等领域得到广泛应用。实现激光雷达点云与图像重建点云的空间配准技术,则是三维重建技术研究的关键。
空间点云配准技术分为初始配准和精确配准2个步骤,初始配准能够初步减小两组点云的旋转和平移错位,精确配准能够使两组点云之间的配准误差最小[7]。目前,最常用的点云配准方法是由Besl和Mckay[8]在1992年提出的迭代的最近点(Iterative Closest Point,ICP)算法。该算法针对目标数据集中的每个目标点,寻找参考数据集中与其距离最小的对应参考点,通过迭代算法估计旋转矩阵、平移向量。然而,该算法存在计算量大、效率低、对初始位置要求高等不足,且忽视了2组点云之间的尺度因子[9]。Chen和Medioni[10]提出点对面搜索最近点的配准方法,降低原始ICP算法对初始位置的要求,加快算法收敛速度。Rusinkiewicz和Levoy[11]详细分析ICP算法各个步骤,并提出相应的改进算法。戴静兰等[12]提出基于曲率特征的改进ICP算法,邹际祥[13]提出基于K-D树(K-Dimensional tree)搜索最近点的方法,加快了最邻近点的查找速度。
本文研究了一种改进的快速多尺度因子(Fast Multi-Scale Registration,FMSR)点云配准方法,该方法引入激光雷达点云和图像重建点云之间的尺度因子,提升空间点云配准技术的配准精度和计算效率,并将该方法最终应用于自研激光雷达系统所得点云数据。初始配准使用基于尺度自适应关键点质量(Adaptive Scale Key Point Quality,ASKQ)的点云特征提取算法[14]提取出关键点,实现关键点的特征提取与匹配,利用特征匹配对计算初始参数,提升初始配准的配准精度。精确配准采用K-邻近(K-Nearest Neighbors,KNN)算法搜索相邻近点,无需对点云进行网格划分,减少算法的运行时间,实现快速、准确的配准。
1 三维点云数据获取系统
三维点云数据获取系统由激光雷达系统和图像采集系统构成,如图1所示。自研三维扫描激光雷达系统包括4个组成单元:激光发射与接收单元、扫描单元、控制单元和测距单元。激光发射与接收单元由激光器、望远镜、光电探测器组成,设计同轴光路采集激光发射脉冲、回波脉冲和触发信号。扫描单元用于实现三维扫描功能,垂直方向360°扫描采用步进电机和45°扫描转镜实现,水平方向360°扫描采用高精度数位云台实现。控制单元的核心部件为现场可编程门阵列(FPGA),用于设置激光器参数、程控增益控制、步进电机控制和数据采集等。测距单元包括自动增益控制电路和时刻鉴别电路。系统具体设计及描述参见笔者团队前期发表的论文[15-18]。

图1 三维点云数据获取系统Fig.1 Three-dimensional point cloud data acquisition system
图像采集系统采用摄像机(型号MER-1070-14U3C)拍摄多视点下的图像。相机镜头(型号M7528-MP2)焦距为75 mm,工作距离为0.3 m到无穷远处。该图像采集系统具有1 070万像素分辨率,图像数据通过USB3.0数据接口传输。
2 基于三维点云的空间配准
基于激光雷达点云与图像重建点云的空间点云配准技术,主要包括点云获取、点云处理和点云融合3个步骤,本文实现点云配准的具体流程如图2所示。首先,激光雷达系统与图像采集系统采集激光雷达点云和二维图像数据,并利用SFM(Structure from Motion)技术从图像中获取三维重建点云。其次,利用ASKQ算法选取关键点,提取关键点特征与匹配。然后,利用提取出的匹配对求解初始配准参数,利用基于快速多尺度因子的三维点云配准算法实现精确配准。最后,进行数值仿真和实验,分析验证算法有效性,评价配准精度。
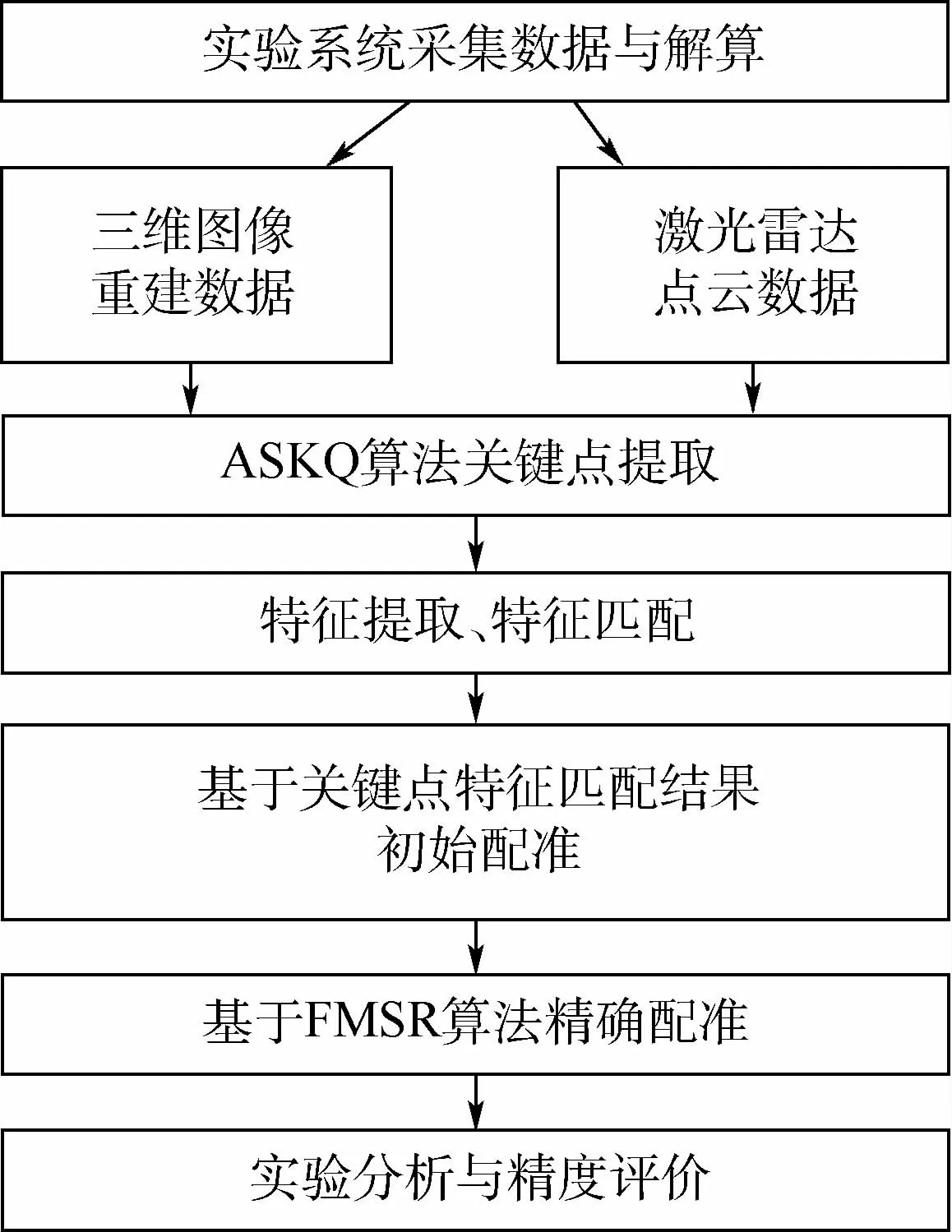
图2 点云配准流程图Fig.2 Flowchart of point cloud registration
2.1 两种点云数据获取
点云数据获取过程包括2个部分:基于三维扫描激光雷达的三维坐标解算和基于图像的三维坐标重建。
为了获取三维扫描激光雷达点云,笔者团队设计了点云实时获取与显示的上位机软件,该软件通过USB接口实时获取测距和扫描模块相关数据,计算每束激光脉冲对应的水平方向扫描角、垂直方向扫描角和激光脚点的距离信息,最后利用激光雷达方程解算出激光脚点的三维坐标。
为了获取图像三维重建点云,首先利用相机拍摄同一物体在不同视角的二维图像。然后基于SIFT(Scale-Invariant Feature Transform)算法提取出图像特征,并基于RANSAC(RANdom SAmple Consensus)算法实现特征匹配。最后利用SFM技术获取三维重建点云。
2.2 基于ASKQ的点云特征提取算法
针对已获取的2组点云,本文采用基于ASKQ的点云特征提取算法提取关键点,评估关键点质量并且排序,从中选取质量最优关键点。该方法的主要步骤如下:
首先,对2组点云中每个采样点v,选取以v的坐标为球心,r为半径的球体内的全部点云信息,并由局部表面矩阵Lj=[xj,yj,zj]T(j=1,2,…,m)表示。
其次,初步选取关键点。利用霍特林变换在局部表面建立局部坐标系,得到2个主轴方向。将每个局部表面矩阵L变换到局部坐标系中,使其与主轴方向对齐,并计算出物理量主轴比δ为

式中:X、Y分别为变换后局部表面矩阵的x分量和y分量。如果δ=1,则该局部表面为普通对称表面;如果δ>1,则为非对称表面。根据采样点v的不同半径rk计算主轴比δk,当主轴比δk中存在极大值,对应的采样点v视为关键点,极大值对应半径rk为最佳尺度。
最后,评估提取出的关键点质量并排序,从中选取最优关键点。关键点质量取决于关键点附近局部表面的主曲率。基于变换后的局部表面矩阵所含数据,进行曲面拟合,得到拟合曲面C,并对曲面C进行n×n的采样,计算关键点质量Qk为
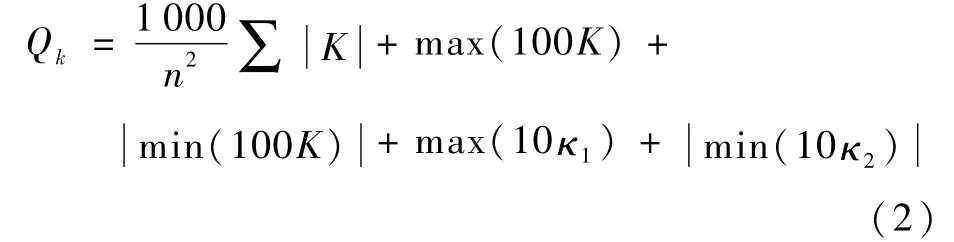
式中:K=κ1κ2为高斯曲率,κ1和κ2为拟合曲面C上每点的主曲率。
将关键点根据关键点质量Qk由大到小排序。由于部分距离相近的关键点容易造成数据信息的重复,因此设置最小距离阈值,消除最小距离范围内的其他关键点,仅保留最优关键点。
2.3 关键点特征提取与匹配
由拟合曲面C采样提取的特征向量具有旋转不变性和尺度不变性,本文选择该特征向量作为形状特征。形状特征的向量维数通常较高,存在占用大量内存、耗费大量时间等问题,因此使用主成分分析(Principal Component Analysis,PCA)方法对形状特征进行降维,将形状特征投影到PCA子空间中。
利用降维后的2组形状特征实现关键点特征匹配。其中,由激光雷达点云获取形状特征为fp,由图像重建点云获取形状特征为fq,两组形状特征之间的误差er为

式中:er在0~π/2之间分布,0代表两组形状特征向量完全相同,π/2代表两组形状特征向量完全不同或正交。当er取得最小值时,则为最佳匹配。
为了实现多尺度点云之间的精确配准,本文对ICP算法引入尺度因子,研究基于快速多尺度因子的三维点云配准算法。该算法选取目标点云与参考点云之间的误差和作为目标函数,最小化目标函数,求解2组点云之间最优尺度因子S、最优旋转矩阵R和最优平移向量T。目标函数为

式中:xk为目标点云;N为目标点云数量;yk为参考点云中与目标点云xk相对应的点。为了保证目标点云中每个点都能在参考点云搜索到对应点,通常选取数量少、精度低的图像重建点云为目标点云,选取数量多、精度高的激光雷达点云为参考点云。
利用2.2节和本节所述的ASKQ算法获取关键点的特征匹配对,计算初始尺度因子S0、初始旋转矩阵R0和 初 始 平 移 向 量T0[19]。当 确 定 初始值后,利用多次迭代实现点云的精确配准。迭代过程如下:
1)对目标点云进行尺度因子为S0、旋转矩阵为R0和平移向量为T0的初始变换,得到变换后的目标点云为xtrans。
2)利用KNN算法全局搜索,在参考点云中搜索与变换后的目标点云xtrans最邻近的点yk,计算出尺度因子Strans、旋转矩阵Rtrans、平移向量Ttrans,使得目标函数误差最小:
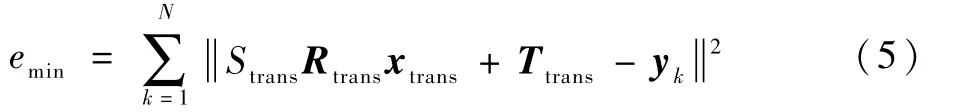

3)两次迭代间参数的变化关系为
将Si+1、Ri+1、Ti+1作为初始值重复步骤1)、步骤2),当尺度因子变化量ΔS=Si+1-Si、旋转矩阵变化量ΔR=Ri+1-Ri、平移向量变化量ΔT=Ti+1-Ti均小于设定阈值时,停止迭代过程,输出即为最优尺度因子S,最优旋转矩阵R与最优平移向量T。
4)利用均方根(Root Mean Square,RMS)误差分析评价配准精度,计算式为

式中:Qrms为均方根误差。
3 实验结果与分析
3.1 仿真实验验证与分析
为了验证ASKQ算法对于关键点提取、特征提取与匹配的有效性,本文使用UWA(University of Western Australia)提供的点云数据库进行仿真实验验证。该点云数据库采用Minolta Vivid 910激光扫描仪,获取真实目标点云,空间分辨率为640×480。本实验选用的数据集包含点云30 165个,点云间隔为0.366 mm。
关键点质量Qk常作为选取高质量关键点的指标。Qk的值越大,表示关键点的质量越高,但相对应的是关键点的数量减小,平坦目标表面上的关键点将被经验性剔除。本实验将阈值设定为Qk>4,将算法中自适应尺度设定为
rk=[2.5 5 7.5 10 12.5]
本实验设置4种尺寸目标(小鸡模型),分别为5、10、20、100 cm,关键点提取的结果如图3所示。结果显示当目标尺寸越大,关键点数量越多,并且关键点分布均匀。
为了验证不同尺度因子的特征匹配实验结果,4种目标尺度因子设置为0.5、1、2、10,尺度因子定义为目标点云与参考点云的比值。基于上述关键点提取结果,进行网格化采样(20×20)得到400维特征向量,利用PCA方法对特征向量降维。匹配结果如图4所示,结果显示该算法对不同尺度因子的目标都有良好的匹配结果。
最后,利用ASKQ算法提取的关键点的特征匹配对计算初始配准参数,并利用FMSR算法实现4组目标的精确配准,配准结果如图5所示。结果表明该算法对4组尺度因子不同的目标均有良好的精确配准结果。
表1为FMSR算法的精确配准结果,从表中得出以下结论:①对尺度因子为0.5、1、2、10的4组目标,利用FMSR算法计算的最优尺度因子S均与理论值μ接近;②由于4组目标具有固定的相对位置,配准得到的4组最优旋转矩阵R一致,最优平移向量T成比例关系,且比例系数与尺度因子相同,表明FMSR算法精确配准结果具有稳定性;③4组目标的配准精度均为0.002 m,说明FMSR算法配准精度具有稳定性;④4组目标的算法运行时间不同,算法运行时间与初始配准的精度有关,初始特征匹配对的精度越高,算法运行越快。

图3 多尺度小鸡模型的关键点提取结果Fig.3 Key point extraction results of multi-scale chicken model

图4 多尺度小鸡模型的关键点匹配结果Fig.4 Key point matching results of multi-scale chicken model
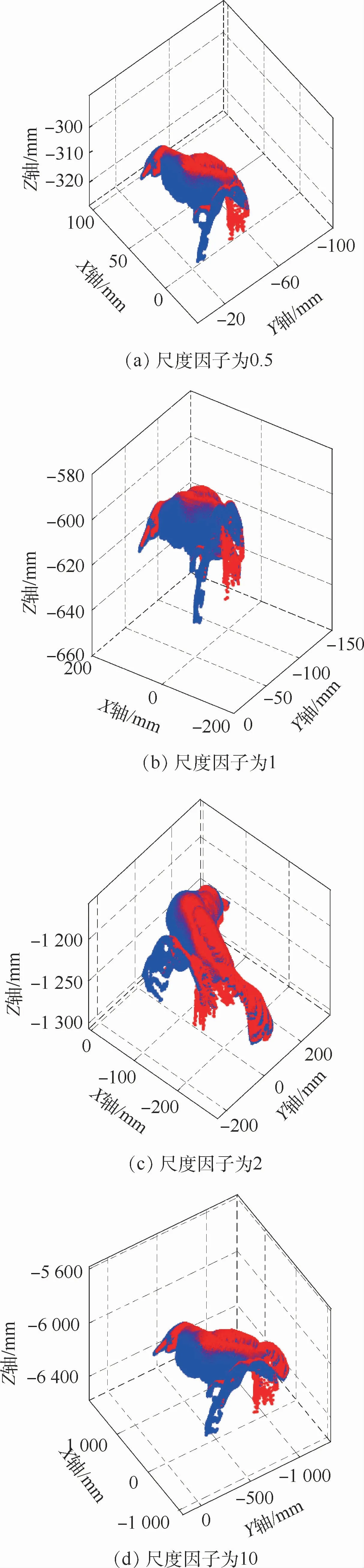
图5 多尺度小鸡模型精确配准结果Fig.5 Fine registration results of multi-scale chicken model

理论值μ 最优尺度因子S 最优旋转矩阵R 最优平移向量T 均方根误差Q rms/m 时间/s 0.5 0.487 (-0.483,0.010,-0.049) (2.659,-145.708,-25.783)0.002 4.043 1 0.977 (-0.483,0.010,-0.049) (5.338,-291.396,-51.402) 0.002 2.601 2 1.954 (-0.483,0.010,-0.049) (10.679,-582.779,-102.807) 0.002 2.509 10 9.768 (-0.483,0.010,-0.049) (53.439,-2 913.906,-513.807)0.002 2.489
3.2 真实实验验证与分析
3.2.1 实验描述
真实场景实验的目标为北京航空航天大学晨兴音乐厅(尺寸为20.30 m×7.85 m×26.56 m),实验场景如图6所示。利用自研三维扫描激光雷达系统采集三维点云,设置激光发射频率为5 k Hz、电机转速为2 r/s、云台转速为0.37(°)/s。获取激光雷达点云28 136个,垂直分辨率为0.144°,水平分辨率为0.185°。采用摄像机(型号MER-1070-14U3C)拍摄多视点图像,图像像素为3 264×2 448,并且利用SFM 技术实现图像三维重建,获取图像重建点云12789个。

图6 北京航空航天大学晨兴音乐厅建筑的实验现场Fig.6 Building experimental site of Chenxing Concert Hall in Beihang University
3.2.2 实验案例分析
本实验中,最小距离阈值设定为Qk>4,自适应尺度的选取范围rk=[25 20 15 10 5 1 0.5]。激光雷达点云和图像重建点云的关键点提取结果如图7(a)和图7(b)所示。由图可知:①关键点仅取决于局部表面的坐标变化,不受目标整体几何形状的影响,因此ASKQ算法提取出的关键点分布均匀。②关键点由局部坐标系提取得出,具有局部不变性,因此关键点鲁棒性佳,不随旋转、平移及尺度因子的变化而改变。③图7(b)中设定的最小距离阈值小于图7(a),因此关键点数量较多。由于图像重建点云密度低于激光雷达点云密度,应从图像重建点云中提取更多关键点,寻找激光雷达点云的最佳匹配。
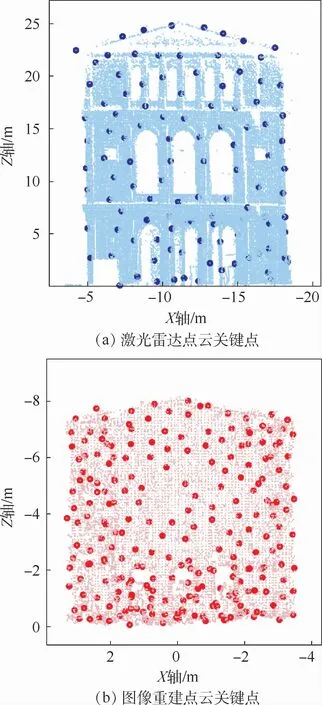
图7 真实场景关键点提取结果Fig.7 Key point extraction results of real scene
通过网格化采样提取出关键点的形状特征,使用PCA方法降维,并对降维后的形状特征实现匹配。本实验提取出关键点的特征匹配对22对,匹配结果如图8所示,结果表明所提出算法具有良好匹配效果。

图8 真实场景的关键点匹配结果Fig.8 Key point matching results of real scene
最后,利用关键点的特征匹配对计算初始尺度因子S0、初始旋转矩阵R0和初始平移向量T0,为FMSR算法提供初始参数,最终通过迭代求解实现精确配准。本文选取S-ICP(Scale-Iterative Closest Point)算法为对比算法,利用所提出的FMSR算法和S-ICP算法配准同一目标。实验目标和2种算法的点云配准结果如图9所示,2种算法配准结果的对比如下:在屋顶上方和墙壁右侧位置,应用S-ICP算法的配准结果存在部分缺失,而采用所提出的FMSR算法则有较优的配准结果。表2结果表明,S-ICP算法的均方根误差为0.325 m,FMSR算法的均方根误差为0.194 m,表明FMSR算法的配准精度高于S-ICP算法,配准精度提高了0.131 m。且运行时间由23.212 s降低为16.207 s,表明FMSR算法能够减小运行时间(30%),提高计算效率。

参数 S-ICP算法 FMSR 算法最优尺度因子S 3.000 3.300最优旋转矩阵R (1.683,-0.035,0.935) (1.561,-0.044,-2.214)最优平移向量T (-39.233,-29.415,2.564) (17.394,12.485,-0.957)均方根误差Q rms/m 0.325 0.194时间/s 23.212 16.207
4 结 论
为了提高激光雷达点云和图像重建点云的空间点云配准精度,自主搭建三维扫描激光雷达系统,主要性能包括:点云垂直角分辨率0.144°,水平角分辨率0.185°,点云密度300 pt/m2(pt/m2代表每平方米的点数);结合基于ASKQ的点云特征提取算法和基于FMSR的点云配准算法,实现激光雷达点云和图像重建点云的初始配准和精确配准。
ASKQ算法为点云配准的初始配准过程提供高质量匹配对,从而计算出精确的初始尺度因子S0、初始旋转矩阵R0和初始平移向量T0,为精确配准提供准确的初始参数。利用FSMR点云配准算法进行精确配准,通过KNN算法对2组点云进行全局搜索,多次迭代计算得到最优尺度因子S,最优旋转矩阵R和最优平移向量T。通过数值仿真和实验结果表明,该算法针对空间目标(20.30m×7.85 m×26.56 m)配准精度达到0.194 m,运行时间为16.207 s。FMSR算法有效提升空间点云配准精度和计算效率(30%)。上述方法可以为空间场景重建和纹理匹配提供算法基础。
