超低信噪比调频连续波引信信号小周期态Duffing振子检测
2019-11-21朱志强侯健闫晓鹏栗苹郝新红
朱志强,侯健,闫晓鹏,*,栗苹,郝新红
(1.北京理工大学 机电动态控制重点实验室,北京100081; 2.北京京航计算通讯研究所,北京100074)
在对调频连续波(FWCW)引信进行欺骗式干扰时,检测并获取其参数对于干扰波形的设计具有重要的参考意义[1]。然而,由于电子对抗的非合作性,到达干扰机的调频引信信号往往十分微弱,且淹没在真实战场环境下的强噪声中,难以被信号侦察系统检测。因此,研究低信噪比(SNR)下的调频连续波信号检测具有重要的现实意义。
有关调频连续波引信信号检测问题,传统的检测方法是基于线性、确定性系统的。文献[2]利用回波信号幅值的变化规律和范围特征进行信号检测,该时域方法虽然简单,但提取的信号特征稳定性不高。经典频域方法,如快速傅里叶变换(FFT)等,由于无法表述信号的时频局域性质,其抗噪性能较差且对调频信号的特征检测能力不足[3-4]。从线性时频域的角度,文献[1,5-6]分别基于改进后的希尔伯特-黄变换(HHT)、Cohen类模糊函数和Wigner-Ville结合Hough变换,利用时频分析方法实现了对单分量和多分量线性调频信号的特征参数识别。文献[7]提出了基于极大chirplet变换的调频连续波信号检测方法,可以用于处理对称三角线性调频连续波信号;但其处理过程较为繁琐、限制条件较多,难以实现工程应用。此外,采用上述检测方法,可达到的最低检测信噪比门限均不足-10 dB[1-8]。可见,在低信噪比下检测调频连续波信号时,传统的线性检测方法在信噪比门限或者实时性方面无法满足要求。
随着非线性科学的发展,混沌理论,尤其是Duffing振子系统,在微弱信号处理方面表现出独特的优越性[9-10]。现有的Duffing振子检测算法的主要思路为设置强参考信号,利用混沌系统处于临界状态时对微弱周期信号的极端敏感性及对噪声的免疫特性,实现对微弱周期信号在超低信噪比下的实时检测[11-12]。由于系统临界阈值受参考信号频率以及噪声强度的影响较大,且单个Duffing振子的测频范围有限,因此传统Duffing振子对大带宽且频率快速变化的调频信号检测能力严重不足。
针对上述问题,本文构建了基于小周期态Duffing振子的微弱信号检测系统模型,并将其应用于低信噪比下的调频连续波引信信号检测方法中。该方法克服了Duffing振子强参考系统的固有缺陷,能够实现低信噪比下大带宽和频率快速变化的连续波调频信号的检测,同时降低了计算成本和时间消耗,为调频连续波引信信号的侦察及参数估计提供了技术支撑。
1 调频连续波引信信号基本特征
以三角波调频引信为例,进行调频连续波引信信号特性分析。其发射信号为

式中:A为发射信号幅度;fc为信号载频;ΔF为信号单边调制带宽;T为调制信号周期,其倒数表示调制信号频率fm;β=4ΔF/T=4ΔFfm为调制斜率;n为调制周期数。
通常,调频引信发射信号载频fc在GHz量级,难以被直接采样和处理。因此侦察设备会对接收到的调频引信信号进行下变频,将其频谱搬移至几十兆赫兹。下变频后信号与式(1)形式基本一致,区别在于幅值A、载波fc数值的变化。因此,仍然用式(1)描述侦察设备截获的调频引信信号。
设经下变频三角波调频信号参数为:载频fc=50 MHz,单边调制带宽ΔF=10 MHz,调制信号频率fm=100 k Hz。其时频特性如图1所示。
可见,三角波调频信号具有频带较宽、信号频率变化较快且频率变化有正负两个不同斜率的特性。这些特性使得非合作条件下的调频引信信号检测方法不仅要具有在噪声下对准周期信号的高度敏感性,同时还要能保证在大带宽和快频率变化率下的检测精度。
2 小周期态Duffing振子检测系统
2.1 可停振动系统
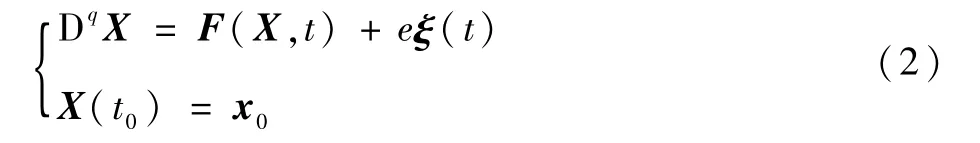
设随机微分方程为
式中:X、F为二维矢量随机过程;q∈R为微分方程的阶数;eξ(t)为系统输入的随机扰动;e为随机扰动幅度;η0为微分方程平凡解(即F(η0,t)=0)。
如果满足以下2个条件:
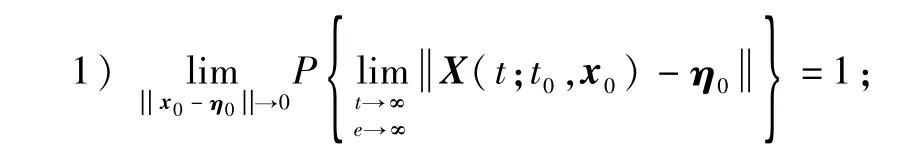
2)当式(2)描述的系统输入为周期及准周期信号时,系统有周期或者是准周期解。
则称式(2)所对应的系统为可停振动系统[13]。其中条件1)表示系统在受到微小随机扰动时,以概率1渐进稳定,其对应的状态称为可停振动状态。由定义可知,可停振动系统的可停振动状态变化对噪声不敏感,对周期及准周期信号敏感,这为检测未知频率的微弱调频信号提供了一条新的思路。
2.2 Duffing振子基本特性分析
经典的Holmes型Duffing振子方程为

式中:k为阻尼比;-x(t)+x3(t)为非线性恢复力;γcos(ωt)为幅值为γ,角频率为ω的强参考信号。随着γ的增加,Duffing振子系统依次经历小周期运动、倍周期运动、混沌运动、大尺度周期运动。
设k=0.5,当γ的值大于临界阈值γc(约为0.826)时,Duffing振子系统将从混沌临界运动状态进入到大尺度周期运动状态。这一转变对参数γ极其敏感,微小的周期扰动就可能改变系统的动力学行为。因此,设置强参考信号使系统处于临界状态时,当系统中存在微小的周期扰动时,相轨迹会呈现出周期性的在混沌态和大尺度周期态间的转换,如图2所示。利用这种转换的周期性实现微弱周期信号检测和频率信息估计的方法称为Duffing振子强参考信号检测法。
Duffing振子强参考信号检测系统可以实现低信噪比下的周期信号检测。然而,将其应用于大带宽和频率变化较快的调频引信信号检测时,存在以下固有缺陷:
1)当强参考信号与待测信号频率非常接近时,系统存在检测盲区,在该区域内系统始终处于大尺度周期态或混沌状态,这意味着无法通过相轨迹的转换来进行信号检测[14]。
2)系统的临界阈值对强参考信号频率以及环境噪声强度敏感,因此需要根据它们的变化来设置合适的临界阈值,这会使检测系统复杂化[15]。
3)单个Duffing振子的频率检测范围较窄,若要实现大带宽频率检测,需设置Duffing振子阵列,导致较高的计算成本和时间消耗。
4)系统相轨迹由混沌态向大尺度周期态转换过程中存在过渡段,对于阵列中的每个振子,都需要较长的时间来确定Duffing振子系统当前的状态转换情况,否则可能导致误判[16]。
2.3 小周期态Duffing振子检测系统模型
为避免上述缺陷,本文提出一种新的混沌检测方法来实现超低信噪比下的调频引信信号检测。该方法在Duffing振子强参考信号检测系统的基础上,把强参考信号置零,将待测微弱信号直接送入Duffing振子系统作为策动力,利用Duffing振子处于小周期态时的相轨迹特征实现微弱信号检测。此时,为了使系统能对待测信号足够敏感,仍在系统内部保留参考角频率ω,其状态方程为式中;I(t)为待测系统输入信号,在进行调频引信信号检测时,其形式通常为A cos(ω0t+˙ωt2)+eξ(t)(ω0为初始角频率,˙ω为角频率变化率,eξ(t)为噪声);(x+1)是为了保证相轨迹以(0,0)为焦点,尽可能均匀地分布在4个象限,以便后续计算。另外,为确保系统工作在小尺度周期态,待测信号幅值A不能超过0.36[17-18]。
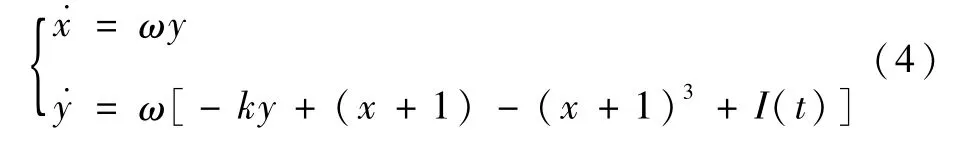
基于Hamilton系统理论,当k>0且I(t)为高斯噪声时,Duffing振子系统(4)满足式(2)的条件1);当k>0且系统中输入微弱的周期信号时,Duffing振子系统(4)是耗散系统[19]。所以,当k>0时,Duffing振子系统(4)是可停振动系统。
根据可停振动系统的定义,可以使用式(4)中Duffing系统作为检测模型。因为输入信号微弱且不存在强参考信号,系统处于小周期态,所以将此系统称为小周期态Duffing振子检测系统。其相比Duffing振子强参考信号系统的主要优势在于:
1)取消了强参考信号,无需进行临界阈值的复杂设置,也不存在检测盲区。
2)单个Duffing振子的频率检测范围大幅扩展,同时能适应频率的快速变化。
3)系统结构及算法简单,既无需判别系统的状态转换,也无需设置振子阵列,大幅降低计算成本和时间消耗。
因此,小周期态Duffing振子很好地克服了传统Duffing振子检测系统的固有缺陷,且在测频范围和算法复杂度等性能上具有明显优势。
小周期态Duffing振子系统在不同策动信号下的相轨迹图如图3所示。图3(a)表示在只由高斯白噪声策动时,系统处于可停振动状态,其相轨迹无规律;图3(b)表示当由微弱调频信号驱动时,系统处于小周期状态;图3(c)表示在信噪比降低到-35 dB时,系统相轨迹虽然变得粗糙,但仍处于小周期态的理想轨迹附近。以上现象验证了本文提出的小周期态Duffing振子系统对微弱调频信号敏感,对随机扰动不敏感的特性。因此,利用图3所示的相轨迹特征,可以在没有强参考信号和不设置临界阈值的情况下,实现微弱调频信号的检测。
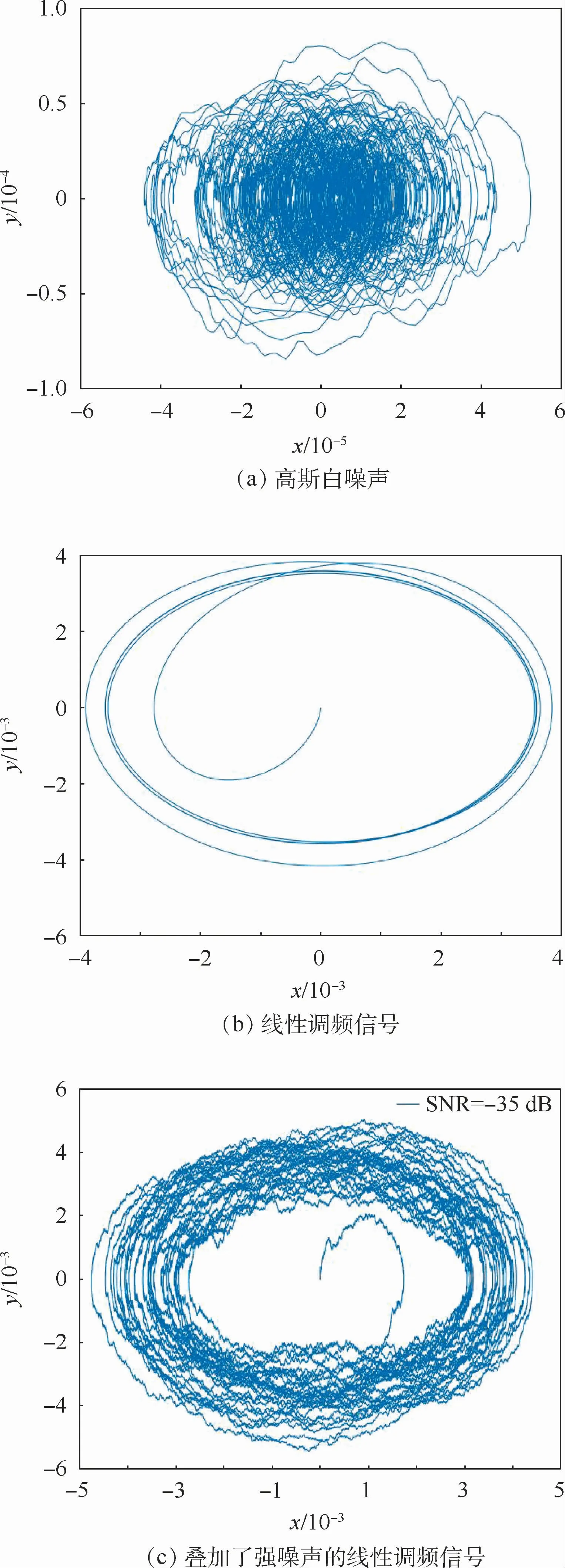
图3 不同输入信号策动下小周期态Duffing振子系统的相轨迹图Fig.3 Phase trajectories of small-scale periodic state Duffing oscillator system driven by different input signals
3 小周期态Duffing振子微弱信号检测方法
3.1 微弱信号检测方法
从图3可以明显观察到,当系统处于可停振动状态时,相轨迹无规律;当系统处于小周期态时,相轨迹的规律性明显。而且,从统计上来看,系统处于小周期态时相轨迹在分布域内的运动周期与待测信号周期相同。受此特点的启发,本文提出一种新的微弱调频信号混沌检测方法。
设φ为Duffing振子系统输出的相点(x,y)对应的相空间角,其正弦和余弦函数为
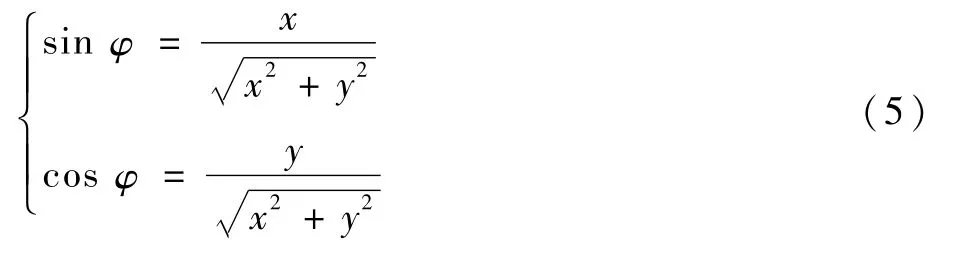
式中:x和y分别表示Duffing振子的位移和速度。相空间角的正、余弦曲线可以用来描述相轨迹的周期特性。
设置系统初值(x,y)=(0,0),将不同信噪比的线性调频信号0.04cos2π(5×107t+4×1012t2)输入小周期态Duffing振子检测系统。图4分别给出了不含噪声和信噪比为-35 d B时的被测信号时域波形与相空间角正、余弦曲线的对应关系。在没有噪声时,信号为准周期信号,同时相空间角的正余弦波形与被测信号的瞬时频率相同(第1个周期除外),如图4(a)所示;在信噪比达到-35 dB时,如图4(b)所示,由于强噪声的影响,已经无法从被测信号时域波形中分辨出信号的特征信息,但正、余弦波形仍然比较清晰并且与图4(a)中周期一致。因此,可以从Duffing振子输出信号的相空间正、余弦曲线中得到其时间-频率特性,进而得到待测线性调频信号的时间-频率特性。
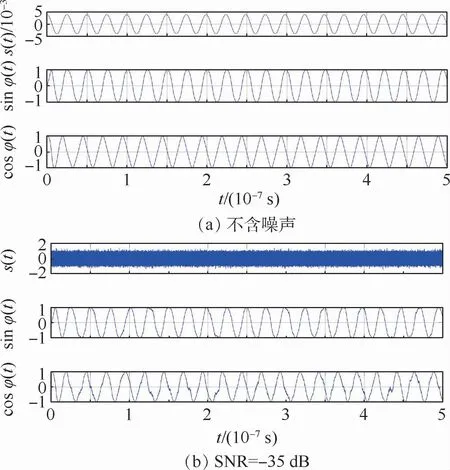
图4 待测信号时域波形和相空间角正余弦波形Fig.4 Time domain waveform of to-be-detected signal and sine cosine waveform in phase spale
在调频连续波引信常用的调制方式中,三角波调制与锯齿波调制本身就是分段的线性调频信号;正弦波调制虽然并非线性调频信号,但由于使用小周期态Duffing振子进行频率检测时,只需要对很短时间内的几个峰值进行检测,在此时间内正弦波调频信号可视为线性调频信号甚至标准正弦波信号。因而,可以使用小周期态Duffing振子实现对连续波调频引信信号在超低信噪比下的检测。
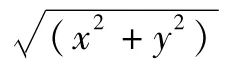
基于上述分析,基于小周期态Duffing振子的微弱调频引信信号检测方法的具体步骤为
1)设Duffing振子系统初值(0,0),阻尼比k=0.5。
2)在预估的待测信号频率范围内选择一个适中值作为参考信号频率f,以保证被测信号与参考信号频率差不会过大。
3)将含噪待测信号输入小周期态Duffing振子检测系统,求解式(4),并计算Duffing振子输出相轨迹的余弦函数cosφ。
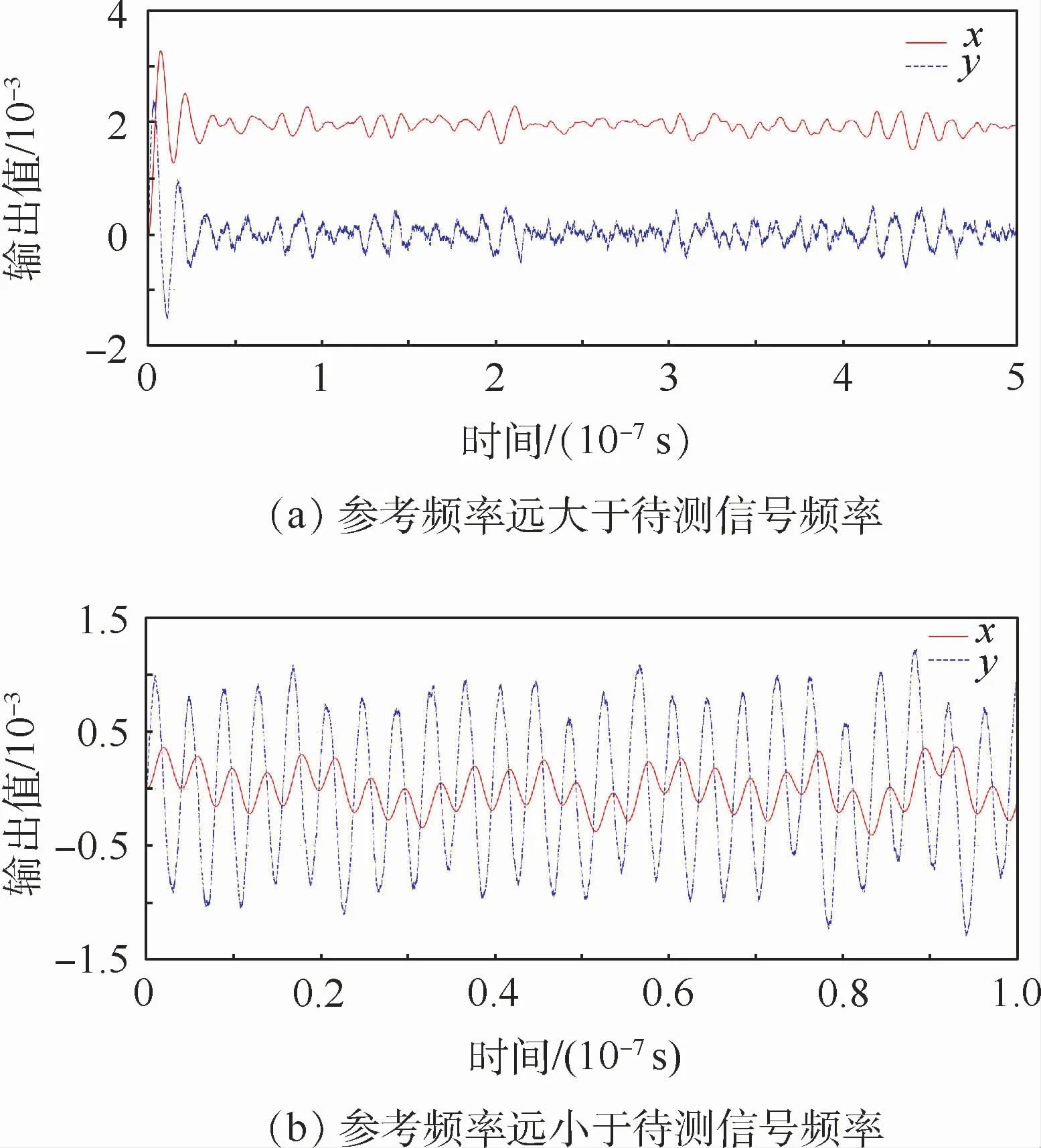
图5 频率差较大时小周期态Duffing振子系统输出的时域波形Fig.5 Time domain waveform of outputs of small-scale periodic state Duffing oscillator system when frequency difference is large
4)利用峰值法找到cosφ所有峰值,测量相邻峰值的时间差,将其倒数视为cosφ的瞬时频率。
5)根据相轨迹余弦cosφ和调频信号同频的原理得到调频信号的瞬时频率。
3.2 性能分析
首先以线性调频引信信号为例,分析此方法的频率检测范围[fL,fH](将频率检测范围[fL,fH]定义为一个频率区间,微弱信号检测系统对初始频率在此区间内的线性调频信号的相对检测误差不大于1%)。设置参考频率f=50 MHz,固定信噪比和频率变化率,设输入的调频信号为
式中:f0为待测信号的初始频率;b为频率变化率。
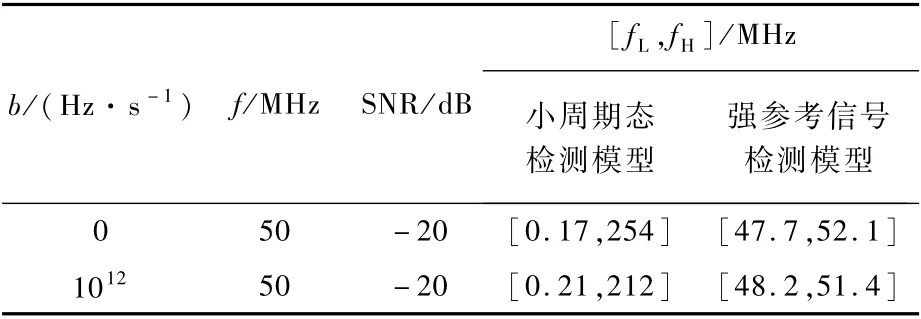
设置信噪比为-20 dB,将频率变化率b=0 Hz/s(标准正弦波信号)和b=1012Hz/s的微弱线性调频信号输入到小周期态检测模型和强参考信号检测模型中,得到单个Duffing振子的频率检测范围[fL,fH]如表1所示。
对于强参考信号的Duffing振子系统检测方法来说,只有当被测信号与参考信号的相对频率差小于0.04时,图2中的周期性状态转换才能稳定出现,因此单振子的频率检测范围较小。而小周期态Duffing振子检测方法则大大扩展了Duffing振子的频率检测区间,仅用单个Duffing振子就能有效地检测出淹没在强噪声下的未知周期信号或宽带调频信号。
随后固定f0=50 MHz,与参考频率相同,在不同信噪比下对不同频率变化率的线性调频信号分别进行20次频率检测仿真,得到的平均检测精度如图6所示。从图6可以看出,虽然在信噪比过低和频率变化速度超出系统检测能力范围时存在个别异常点,总体来说频率检测精度η随频率变化率的增大和信噪比的降低而减小;当频率变化率b在0~5×1012Hz/s的范围内时,信噪比不低于-25 dB时,初始频率的检测精度可以达到99%以上;当信噪比降低至-30~-45 dB时,只要b的取值仍在5×1012Hz/s以下,依然可以保证较高的频率检测精度。
[f L,f H]b/(Hz·s-1) f/MHz SNR/dB/MHz小周期态强参考信号检测模型0 50 -20 [0.17,254] [47.7,52.1]检测模型1012 50 -20 [0.21,212] [48.2,51.4]
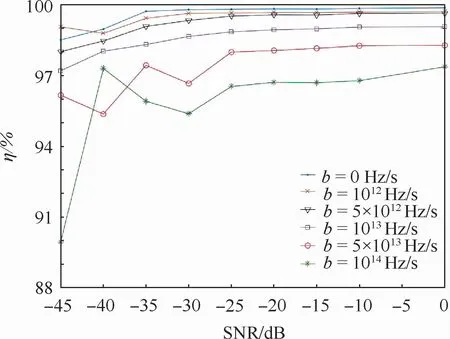
图6 线性调频信号的频率平均检测精度与信噪比和频率变化率的关系Fig.6 Relationship among average frequency detection accuracy,SNR and frequency slope of chirp signals
4 实验验证
为了验证基于小周期态Duffing振子的微弱信号检测方法在调频引信信号检测上的效果,本文使用3种不同调制方式的引信仿真模型及某型号调频引信的辐射信号对此方法进行验证。
首先以三角波调频引信模型为例,设置仿真工作参数如下:三角波调制频率fm=100 kHz,单边调制带宽ΔF=10 MHz,载波频率fc=50 MHz,信号幅值A=0.004,噪声强度为0.0008(-20 dB)。
图7给出了-20 dB信噪比条件下此信号时域波形及采样率为1 GHz、点数为20 000点时的频谱图。由于噪声的影响,已经无法获取三角波调频信号的时域波形和频率特性。如果进一步增大采样率到10 GHz时(200 000点),虽然能够获得较高的处理增益,可以检测到信号的存在,但是大点数FFT存在运算量大、频谱资源浪费的问题,无法满足实时性检测的需求。
图8分别给出了-20 dB的信噪比条件下,采用Duffing振子强参考信号阵列检测方法[20]及本文方法检测得到的三角波调频引信信号的时频特性曲线。根据图8(a),在-20 dB信噪比下,Duffing振子强参考信号阵列检测法得到的时频特性曲线中存在多处频率真实值与测量值相差较大的异常点;根据图8(b),本文方法可以很好地对三角波调频信号进行时频分析,得到的时频特性曲线与真实时频特性曲线几乎重合。因此,本文方法对于三角波调频引信信号的检测效果优于Duffing振子强参考信号阵列检测方法。同时,根据时频特性曲线对调频信号特征的表征能力,基于图8(b)获得的时频特性曲线,可以直接实现调频引信信号的特征参数(如载频、调制频率、最大频偏以及调制类型等)估计。
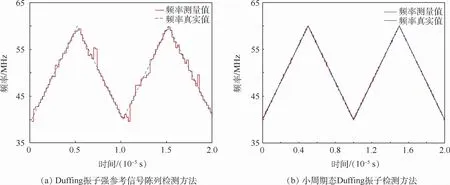
图8 -20 dB信噪比下三角波调频信号时频特性Fig.8 Time-frequency characteristics of triangular wave frequency-modulated signal while SNR is-20 dB
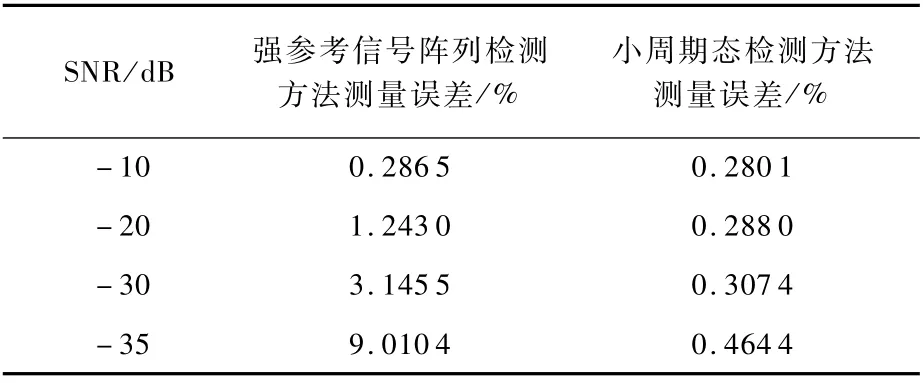
SNR/dB 强参考信号阵列检测方法测量误差/%小周期态检测方法测量误差/%-10 0.286 5 0.280 1-20 1.243 0 0.288 0-30 3.145 5 0.307 4-35 9.010 4 0.464 4
表2为采用Duffing振子强参考信号阵列检测方法和本文方法时,不同信噪比条件下对三角波调频引信信号的频率检测误差。随着信噪比的降低,两种方法的频率检测误差都不断增大,但是当信噪比不小于-35 dB时,本文方法均可以得到高于99%的检测精度,远高于Duffing振子强参考信号阵列推测方法。
为了进一步验证本文方法对不同调制类型的调频连续波信号检测的有效性,在相同的载波频率和调频带宽的基础上,分别对三角波、锯齿波和正弦波调制3种不同类型的调频连续波信号进行检测。
图9为-35 dB信噪比条件下3种调频连续波引信信号的时频特性图,可以看出尽管图像中由于强噪声的影响出现了许多瑕疵点和测量不准确的点,但是频率的平均测量误差均小于1%,证明该方法能实现超低信噪比下对三种调频引信信号的高精度检测。
采集某调频引信真实辐射信号,并加入噪声后,对本文方法进行进一步的半实物仿真验证。此引信的载波频率约为915 MHz,调制频率和最大调制频偏分别约为960 kHz和8 MHz。如图10可知,在-20 dB的信噪比下,利用小周期态Duffing振子可以得到较好的引信检测效果。
为了进行检测能力的量化评估,将该引信信号下变频至50 MHz,以未人为加入噪声时引信信号的频率检测结果作为真实引信频率,计算不同信噪比下的相对检测误差如表3所示。
由于直接对引信辐射信号进行射频采样,采集到的信号存在失真,同时在采集、下变频和滤波过程中也会引入噪声,因而真实引信信号的信噪比检测阈值高于仿真结果。即使如此,本文方法在-30 d B的超低信噪比条件下,对真实调频引信信号依然具有较高的检测精度。至此,小周期态Duffing振子微弱调频引信信号检测方法的超低信噪比和高精度检测性能得到了充分验证。

SNR/dB 测量误差/%-10 0.2824-20 0.494 5-30 0.652 8-35 1.1136
5 结 论
本文在分析调频连续波引信辐射信号特征的基础上,基于可停振动系统理论,提出了一种小周期态Duffing振子混沌检测方法,实现了对微弱调频引信信号的检测。理论分析与实验结果表明,该方法不仅能够克服Duffing振子强参考信号系统的固有缺陷,而且提高了实时性,并扩展了单个Duffing振子的测频范围,具有对调频引信信号的超低信噪比和高精度检测能力,对强噪声环境下非合作辐射源信号侦察具有重要参考意义。
