下承式系杆拱桥合理吊杆力初步确定的方法

潘路杰

【摘 要】下承式系杆拱桥在不同吊杆力的作用下，内力与位移是完全不同的。本文以现有的几种确定合理吊杆力方法为基础，运用midas软件中的未知系数法功能，结合实际工程进行分析比较，确定合理成桥索力，为下一阶段的优化及求解施工阶段的吊杆索力提供可靠的理论数据支撑。

【關键词】刚性连续梁法;刚性吊杆法;最小弯曲能量法;未知系数法

中图分类号： U448.22 文献标识码： A文章编号： 2095-2457（2019）25-0008-002

DOI：10.19694/j.cnki.issn2095-2457.2019.25.003

0 引言

系杆拱桥是内部超静定的梁拱组合结构，拱肋的水平分力由系杆承受，因此系杆拱桥在外部是静定的。考虑吊杆作用，系梁可以认为是一个收到多个弹性约束的拉弯构件。结构活载的传力方式是由桥面系传递至中横梁，横梁传递至系梁，系梁通过吊杆传递至拱肋，最后传递至支座。

吊杆是连接拱与梁的重要构件。吊杆力的选取是否适当，将直接影响到全桥的内力分布与成桥线形，若选取错误，可能会危及到桥梁的舒适性及安全性，吊杆力的疲劳应力过大也可能导致结构的耐久性寿命。因此，如何通过理论计算确定成桥索力，并在实际工程中通过调索将吊杆张拉力调整至具体设计数值，是系杆拱桥设计、施工、监控中的重中之重。

1 几种分析方法简述

1.1 刚性支撑梁法

刚性支承连续梁法就是求解桥梁在恒载作用下的一组吊杆力，使得张拉吊杆后，系梁与吊杆连接处节点位移为零。在确定吊杆力时，主要以位移为控制目标，以保证张拉后桥梁的成桥线形。系梁上弯矩的正负弯矩交替，且均不大，与多跨连续梁结构的弯矩图基本一致，当弯矩足够小时，系梁可以近似的认为是轴心受力构件。

1.2 刚性吊杆法

该方法要求求解一组吊杆力使得吊杆与系梁、拱肋连接处的节点的相对位移为零。从整体受力的概念考虑，通过调整吊杆力的大小，协调梁拱两者之间分配恒载的比例，从而使得桥梁恒载尽量由拱来承担，其实质是梁拱的应变能之和最小。

1.3 最小弯曲能量法

最小弯曲能量法是将位移或者弯矩作为确定合理成桥状态的主要变量，进而求解一组吊杆力的方法。一座系杆拱桥的建成，需要经过复杂的施工过程，理论计算与实际往往会有偏差，采用单一的变量来控制是不合适的。我们可以以系梁的弯曲能量作为目标函数，建立多个约束条件（结构位移、结构弯矩）作为求解一个合理结构的边界条件，进而找寻我们所需要的最优解。

2 工程实例

2.1 工程概况

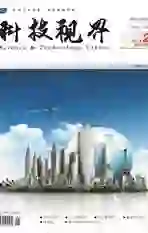
某简支62m跨径下承式系杆拱桥，结构简图详见图1。

上部结构由钢管拱肋、预应力混凝土系梁与横梁、柔性吊杆及整体化桥面系组成。

拱肋：拱肋采用矩形钢管拱，拱肋宽1.5m，高为1.6m，钢管壁厚22mm;拱肋内设吊杆固定端锚具。拱肋高12.4m，矢跨比f/L=1/5，拱轴线为二次抛物线。

系梁与横梁：系梁与横梁采用预应力混凝土结构，C50混凝土。系梁采用矩形断面，为1.7m（宽）x1.8m（高）;中横梁为T形断面，梁高1.8m;端横梁采用箱形断面，高度3m。

吊杆：吊杆顺桥向间距5m。

2.2 有限元模型

采用midas/civil 2019（v1.1）软件进行建模计算，静力计算模型中除了柔性吊杆采用桁架单元外均采用梁单元模拟，中横梁及人行道挑臂采用考虑混凝土有效分布宽度的T形截面模拟，剩余桥面板荷载以均布荷载形式作用于中横梁。全桥共离散为356个节点，419个单元，其中桁架单元24个，梁单元395个。恒载主要包括自重，二期、吊杆张拉力以及预应力荷载。计算模型及边界条件如图2所示。

2.3 计算结果

根据第二章所述，对三种不同的方法进行分析比较：

第一种：约束吊杆与系梁连接节点位移，考虑到桥梁为高次超静定结构，约束过大容易产生较大的二次力，故节点位移按照允许值±0.1mm控制。

第二种：将吊杆截面积放大100倍，自重减小100倍的方式模拟刚性吊杆，以保证吊杆上下端拱肋与系梁位移的一致性。

第三种：同时控制系梁跨中内力与连接节点位移。弯矩按照±700kn·m，位移按照±3mm控制。

根据三种不同的方法，得出吊杆力、梁拱位移差及系梁弯矩如下所示。

由表1可知，刚性支撑梁法及刚性吊杆法的吊杆受力并不均匀，标准差分别为22.45与18.63，而由最小能量法得出的吊杆力较均匀，标准差仅为10.52。吊杆力误差最大的为最边缘的短吊杆，第一种分析方法得出的吊杆力仅为其他吊杆力的1/4，究其原因主要是6#吊杆过于靠近支点，拱肋的重量主要由桥墩承载，支座及桥墩对竖向力起到了很大一部分的分担作用。在我们实际的工程中，这样的吊杆力显然是不合理的，我们总是希望各吊杆能够受力均匀，这样对设计、施工以及结构的受力都是较为合适的。

而从系梁的弯矩图来看，刚性吊杆法的正弯矩较大且全跨径有分布，基本均大于1000KN·m;刚性支撑梁法得到弯矩在跨中极小，但由于6#短吊杆张拉力太小，在该处系梁的正弯矩变化极大，达到近2140.5KN·m，到边支点后又变化为-688.3KN·m;采用最小能量法得到的弯矩是介于两者之间的，在设定跨中弯矩范围的时候是按照700KN·m控制的，实际大部分弯矩均小于300KN·m，由于边吊杆力的张拉，导致6#吊杆处的正弯矩向支点处转移，支点处弯矩最大值为1809.5KN·m，拱脚处横梁根据受力需要加高至3m，故将系梁的最大弯矩调整至支点处是符合拱桥受力特点的。

3 结语

本文基于刚性支撑梁法、刚性吊杆法及最小能量法三种分析方法对简支下承式系杆拱桥在恒载作用下的吊杆力进行分析计算，得出初步的成桥索力。

最小能量法充分考虑了长短吊杆及主拱肋与主梁的变形协调能力，可以较好地弥补刚性支撑梁法与刚性吊杆法求解合理成桥索力的局限性，可应用于下一阶段正装倒拆模型中，在工程中有较好的参考性。

【参考文献】

[1]曹晨瑞，史进.最小弯曲能量法确定系杆拱桥成桥索力[J].兰州工业学院学报，2014，21（03）：40-43.

[2]张燕青.确定系杆拱桥合理吊杆索力的方法及其应用[D].浙江大学，2014.

[3]陈旭，宁晓骏，张清旭.下承式系杆拱桥成桥索力的确定[J].中国水运（下半月），2018，18（12）：205+208.

[4]叶建龙，孙建渊，石洞.梁拱组合桥柔性吊杆张拉力的确定及分析[J].城市道桥与防洪，1999（04）：21-24+50.