米槁种群树高-胸径关系研究
2019-11-19刘济明程晶李丽霞李佳
刘济明,程晶,李丽霞,李佳
(贵州大学林学院,贵州 贵阳 550025)
米槁(CinnamomummigaoH.W.Li)又名大果木姜子,属樟科樟属常绿乔木[1],主要分布于贵州、云南和广西等地,是我国的特有树种,贵州十大苗药之一,有很好的应用和开发前景.种群结构是种群最基本的特征,主要包括年龄结构、径级结构、高度结构等,它既可反映种群内不同大小个体数量的分布和配置状况,也能反映种群的数量动态及其未来发展与演变趋势[2-3].其中年龄结构包括增长型、稳定型和衰退型3种类型.当前,对米槁树种的研究多从其化学成分、生理特性等方面进行试验研究[4-5],而对米槁种群树高-胸径关系研究甚少.由于米槁年龄结构数据不易得到,所以研究过程中多采用径级结构代替年龄结构进行试验分析.
树高、胸径和树种是了解树木状态的重要因子,是反映树木生长情况的主要数量指标[6].在林业调查中,关于林木生长、材积和林分动态变化,单木的树高和胸径是2个极其重要的测量要素[7-8].树高-胸径相关模型能够反映出树高随胸径的变化规律,亦称为树高曲线方程.目前,在林业研究中已经有了大量的树高曲线模型,并被广泛应用在各个地区和不同树种上[9-12].树高-胸径的关系一直是研究的热点,因此许多研究者对林木的胸径、树高的生长规律及相关关系进行研究[13-15].比如对思茅松(Pinuskesiyavar.langbianensis) 、马尾松(Pinusmassoniana) 和杨树(Populus) 等树种的树高与胸径相关关系的研究也较多[16-17],并建立了相应树种生长的预测模型.树高与胸径有较强的相关关系,在实地测量胸径比较简易而准确,而测定树高是比较难的,而且测量数据不精确,即使在同一样地内,由于长势不同,胸径和树高的生长差异显著[18].研究者们从不同角度研究树高-胸径相关关系差异,认为树木的树高-胸径关系与其所处生境类型和林分密度有相关关系[19].
本文根据对米槁种群采样的实测数据,研究米槁种群结构的变化规律,并通过11种模型对米槁种群的树高-胸径关系进行拟合,分析其相关性,从而确定适用于米槁种群的树高-胸径的最优拟合模型;并对其可靠性进行拟合精度检验,构建最合适的模型,为后续树种分布研究以及经营与管理提供科学的理论依据.
1 研究区概况
研究区(N 25°00′21″~25°29′18″,E 105°40′07″~108°15′17″)位于贵州省罗甸县、荔波县、册亨县、贞丰县、望谟县、镇宁县[20].气候类型为亚热带季风湿润气候,气候垂直差异明显,雨水充沛,有较长的雨季且雨热同期,夏季高温多雨,冬季低温少雨,而春秋季界限不分明.该区域内地形起伏较大,以山地高原为主,地貌类型复杂多样,自然环境较好.米槁林均分布在其坡位上部、中部、下部,其中以中坡位分布较多,其坡度基本为陡坡(表1);岩层主要多为板岩、石灰岩、砂页岩及第四纪红色豁土,土壤类型为红壤、黄红壤、山地黄棕壤、石灰土[21].该调查区域的海拔在652~1 022 m之间,年平均温度为16.5~20 ℃,极端最高温在40 ℃左右,年平均降水量为1 100~1 335 mm,无霜期283~339 d.
该区域立地条件较好,植物种类繁多,乔木层主要包括枫香(LiquidambarformosanaHance.)、猴樟(CinnamomumbodinieriLevl.)、赤皮青冈(Cyclobalanopsisgilva(Blume) Oersted)、九里香(MurrayaexoticaL.Mant.)、小叶石楠(Photiniaparvifolia(Pritz.) Schneid.)、香叶树(LinderacommunisHemsl.)等;灌木层主要包括毛桐(Mallotusbarbatus(Wall.) Muell.Arg.)、藤构(BroussonetiakaempferiSieb.var.australis Suzuki)、油茶(CamelliaoleiferaAbel.)、山鸡椒(Litseacubeba(Lour.) Pers.)、杜茎山(Maesajaponica(Thunb.) Moritzi.ex Zoll.)、山莓(RubuscorchorifoliusL.f.)等;草本主要包括杜若(PolliajaponicaThunb.)、东风草(Blumeamegacephala(Randeria) Chang et Tseng)、金毛狗(Cibotiumbarometz(L.) J.Sm.)等.
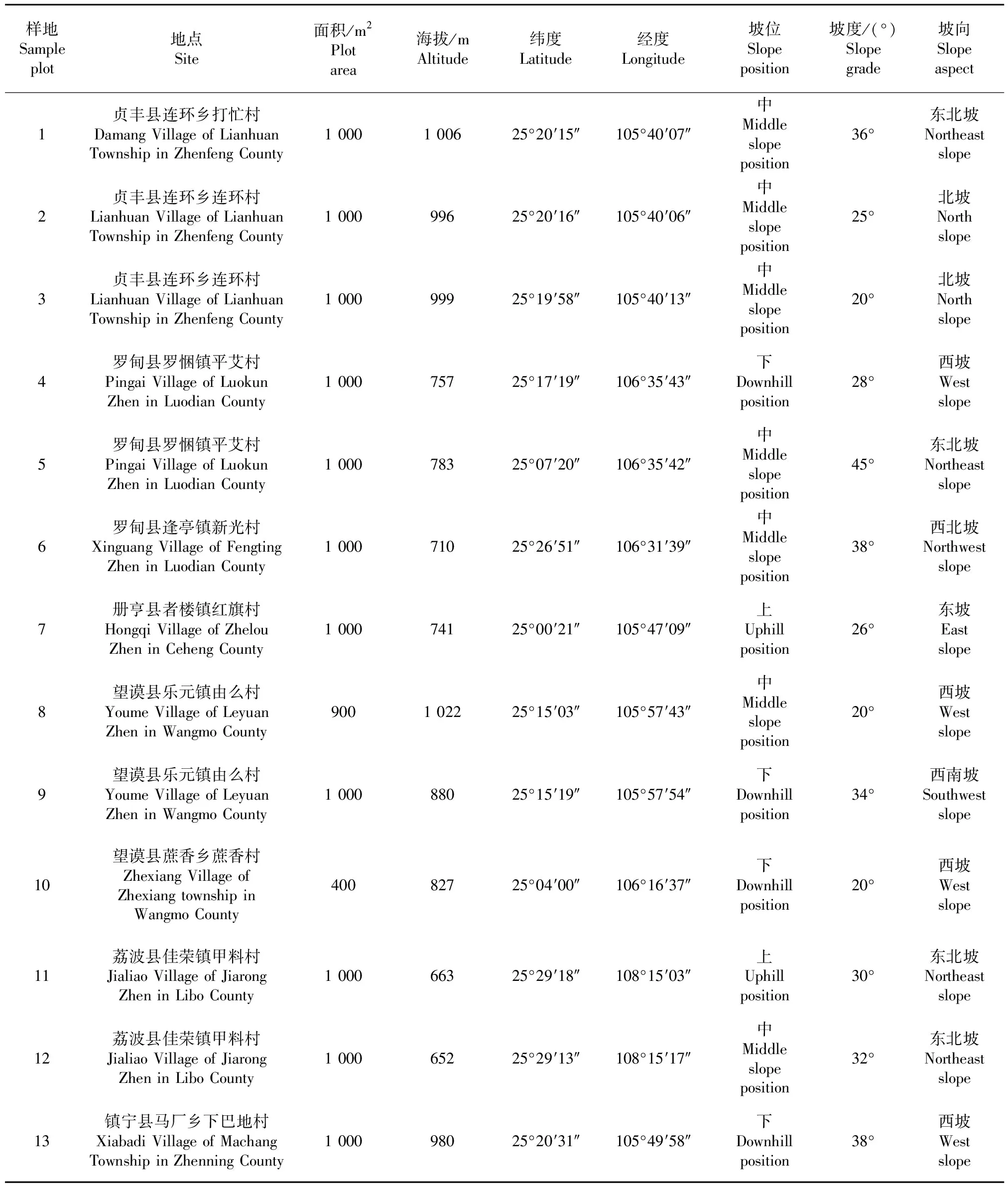
表1 米槁种群调查地的概况
2 试验方法
2.1 数据来源与统计
数据来源于2016 年6~9 月对贵州省米槁天然林分布进行实地调查,选择米槁天然林分布集中且人为破坏较少的地点(罗甸县、荔波县、册亨县、贞丰县、望谟县、镇宁县)进行样地调查,共调查样地13 个,调查总面积12 300 m2,包括乔木样方123个.调查样地内的米槁所有高度小于或等于50 cm的定义为米槁的幼苗阶段,高度大于50 cm且胸径小于4 cm的定义为米槁的幼树阶段,胸径大于等于4 cm的米槁定义为成树[20].在调查的乔木样方中进行每木检尺,分别测量乔木的树高、胸径、枝下高等数据[22].
2.2 试验方法
采用空间代替时间的方法,由于植株的径级结构能够反应该种群个体在各个方向上的配置差异[23],所以用米槁的径级结构代替年龄结构,其中选取米槁种群不同径级(幼苗幼树、小径木、中径木、大径木)所占的比例作为指标.小径木4~8 cm径级,中径木8~24 cm,大径木≥24 cm径级.依据米槁生活史特点,将米槁按胸径大小分级,每级间隔4 cm,即1径级是0~4 cm,2径级是4~8 cm,3径级是8~12 cm,以此类推[24].根据样本调查可知米槁树高可达32 m,并将其树高以2 m为1步长,即0~2 m 为1个梯度,2~4 m为1个梯度,以此类推.
并根据米槁树高、胸径实测数据,选用11个具有代表性且具有生物学意义的曲线模型对米槁种群的树高-胸径进行曲线拟合,并对模型参数求解,分析树高-胸径的相关性;并采用T检验验证拟合精度,从中筛选出拟合优度较高的模型.
2.3 模型构建
用11种生长曲线模型来拟合米槁种群树高-胸径的相关关系,筛选出拟合优度较高的模型.模型公式见表2.得出参数后选择最优拟合模型,并确定拟合函数,采用T检验的方法检验最优拟合精度值.

表2 11 种生长曲线模型公式
2.4 数据处理
运用Excel2010和SPSS 18.0进行数据处理及统计分析,得出米槁种群胸径和树高的分布规律,以及树高-胸径相关性的分布状态.根据曾翀[25]从国内外文献中筛选的31种树高模型中,选用11种模型进行拟合分析,从中筛选出拟合优度较高的模型,得出模型参数,并分析其相关性.
3 结果与分析
3.1 米槁种群树高和胸径的分布规律
由图1可知分布出现2次明显的下降,其分界范围在树高为8~16 m之间,且在12 m的树高时分界最明显.总体趋势分布为米槁种群株数比例在0~12 m的树高范围内随着树高的增长而逐渐减少,之后数量增加,在12~32 m的树高范围内继续减少.米槁种群株数比例在树高为0~2 m之间最高,比例为43.98%,也就是在幼树幼苗阶段时米槁数量最多;而米槁种群株数比例在树高为28~32 m之间最低,其比例为1.39%,这说明米槁处于过成熟林阶段时数量逐渐减少.其中树高为2~4、16~20 m的株数比例相同,均为10.65%,表明米槁种群由成树过渡到成熟林的过程中,即使种群数量有减少的趋势,也有可能达到成树阶段的种群数量.
在米槁种群胸径分布上,选取不同径级的株数来分析米槁种群不同胸径阶段的数量分布规律,影响小且结果更精确.由图1可知,米槁种群数量随胸径分布整体上波动幅度随着胸径的增加,其株数比例逐步减少,基本呈现下降趋势.其中米槁种群数量在胸径为0~4 cm范围内,也就是在幼苗幼树阶段株数比例最高为54.17%,显著高于其他所在胸径占的比例.而胸径4~8 cm的小径木,其株数比例为8.33%,胸径8~24 cm的中径木比例为12.50%,胸径大于24 cm的径木比例为25.00%,其中大径木中胸径在52~56 cm的一般最大径级的比例为0.93%,胸径介于56~64 cm的比例为0,且胸径为64~68、72~76、大于76 cm的米槁株数所占比例仅为0.46%,也大致趋近于0.由此表明,米槁种群的幼苗幼树阶段所占比例大于之后的所有径级的株数所占的比例之和.
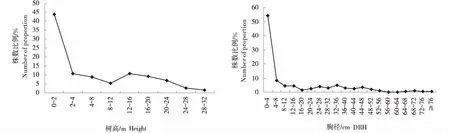
图1 米槁种群树高胸径的分布规律Figure 1 Tree height and DBH distribution in Cinnamomum migao population
3.2 米槁种群树高与胸径数据分析
选取米槁种群乔木层的胸径树高的实测数据做散点图进行分析,如图2所示.米槁种群的胸径处于0~115 cm之间,胸径均值为26.71 cm;米槁种群的树高跨度范围从0~32 m,树高均值为15.59 m,最大值为32.00 m,标准差为7.35 m,并根据图2中拟合的曲线可见米槁种群树高胸径的分布具有一定的相关性.由此进一步表明米槁种群树高和胸径的分布呈正相关,即随着胸径的增加,树高增加,胸径数据集中在0~120 cm范围内,最大值为113.1 cm.由于本研究是采用空间代替时间的方法,即用米槁的径级结构代替年龄结构,用不同径级的米槁代表胸径来拟合出树高曲线模型.因此,根据采集的米槁种群比较均匀,有不同树龄的样本数据,可间接表明米槁种群的树高和胸径符合树木不同年龄的生长状态,没有明显的聚类中心分布.
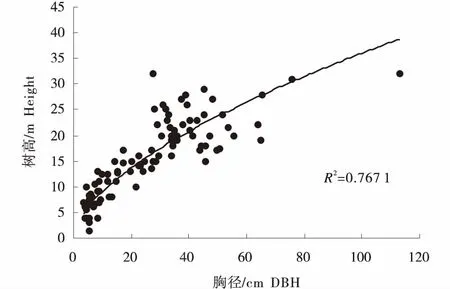
图2 米槁种群胸径树高分布散点图Figure 2 Scatter plot of tree height and DBH distribution in Cinnamomum migao population
3.3 基于11种生长模型的树高-胸径曲线拟合
根据对米槁种群乔木层的胸径树高的实测数据做散点图进行分析后,采用SPSS 18.0回归分析功能建立米槁种群树高与胸径的最优模型,将树高、胸径的实测数据分别代入11个生长曲线模型中进行拟合.得到的米槁种群11种树高-胸径生长的模型曲线与散点综合分布图的曲线拟合如图3所示.得到的米槁种群的曲线模型各参数、模型的判定系数(R2)如表3所示,通过比较可知,复合模型、增长模型、指数函数模型和Logistic模型等拟合效果不理想,米槁树高-胸径拟合模型相关系数R2最高的是幂函数模型,为0.777;其次是三次多项式函数的拟合模型判定系数(R2)为0.767,以及对数函数的拟合模型判定系数(R2)为0.762,而其他8种函数曲线模型拟合效果较差,R2较低.因此,基于R2统计量可看出幂函数模型拟合效果好.
由图3可知,幂函数模型曲线和散点分布的重合度均优于其他10种曲线模型的拟合.三次多项式函数曲线在胸径40~80 cm之间有明显的离散现象,没有趋于该模型曲线,会造成预估值的偏小,但其胸径在110~115 cm之间,三次多项式函数曲线的预估效果要稍好于幂函数的预估效果;而对数函数曲线在胸径45~70 cm之间也有离散现象,同样也可能造成预估值的偏下.因此,在曲线拟合上可看出幂函数曲线比其他10种曲线模型拟合效果好.
通过进行各曲线函数模型的回归模型方差检验(ANOVA检验)如表4所示,11种回归模型的Sig.均小于0.01,说明各曲线模型均在0.01水平上极显著,树高-胸径两者相关性较好[26],模型成立的统计学意义重大.幂函数模型的残差平方和为8.035,均方为0.081,通过比较可知,幂函数的残差平方和以及均方都小于其他10种曲线函数模型的残差平方和均方,由此说明采用除幂函数模型的其他10种曲线函数模型计算出来的拟合值和实际值的差值较幂函数大,间接说明幂函数模型拟合效果较好.由表3可知,幂函数模型的常数是2.255,回归系数是0.602,由此得出拟合效果最好的树高曲线模型为:
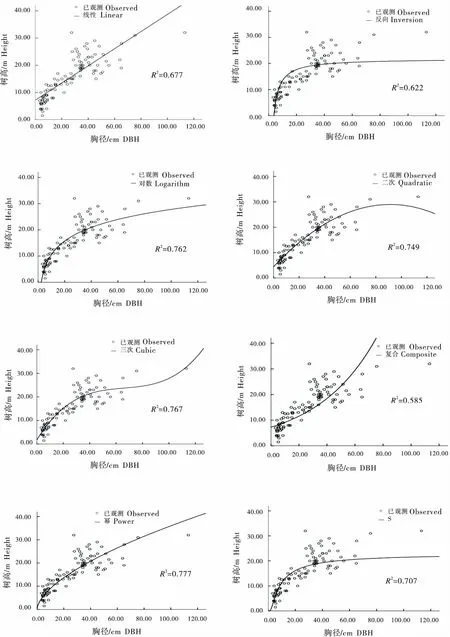
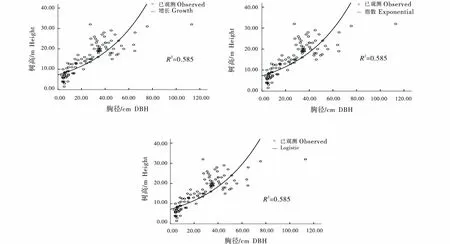
图3 不同模型的米槁种群树高-胸径拟合曲线Figure 3 Tree height-DBH fitting curves for different Cinnamomum migao population models
lnH=2.255×D0.602;(R2=0.777)
这说明随着D以0.602次方的指数函数形式增长,H值也相应地变化增长.由图3可知三次多项式函数模型和对数模型的拟合效果也较好,但不如幂函数模型拟合效果好;而二次多项式函数模型和S模型的判定系数R2也较高,但拟合效果却一般;并且其他曲线模型判定系数R2也较低,拟合效果较差,其残差平方和和均方也较其他模型相差较大,由此整体表明幂函数模型拟合效果最好.
综合而言,根据判定系数(R2)、11种曲线模型的拟合以及回归模型的方差检验得出的残差平方和和均方值这几个指标共同表明,幂函数拟合模型优于其他10种模型,所以,米槁种群树高-胸径的关系应选幂函数模型为最优拟合模型.
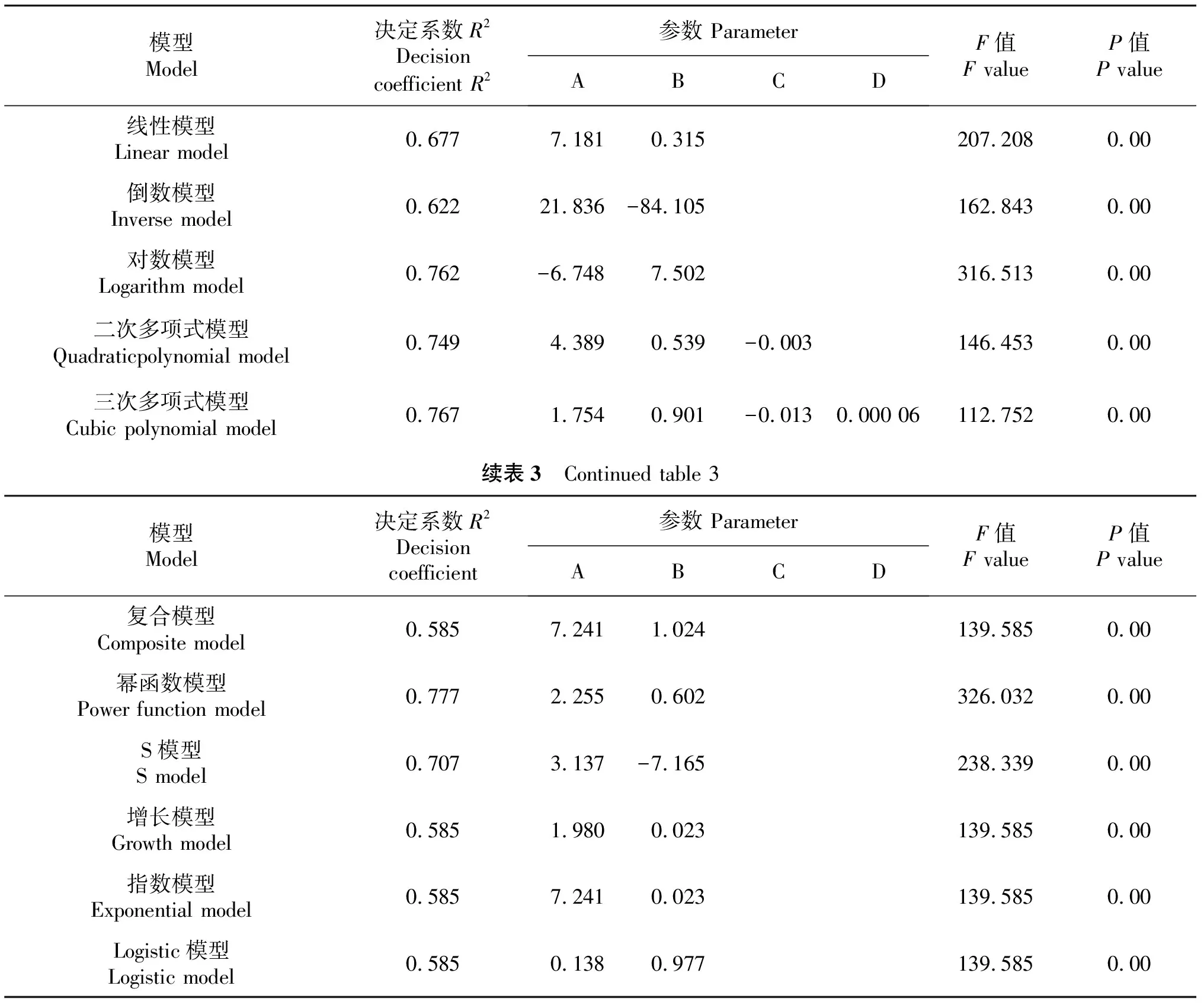
表3 米槁种群树高-胸径的11种模型拟合结果
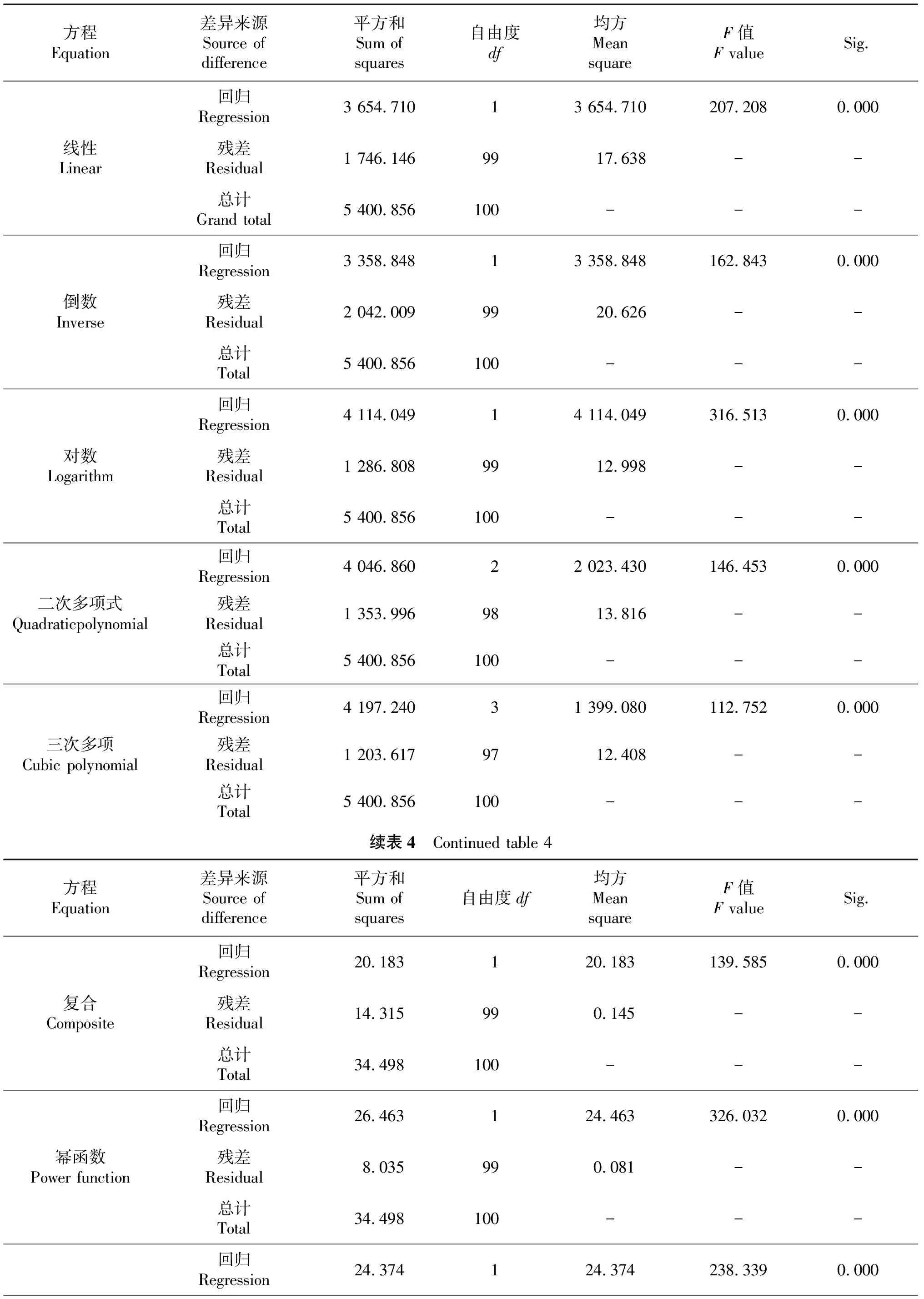
表4 回归模型的ANOVA检验
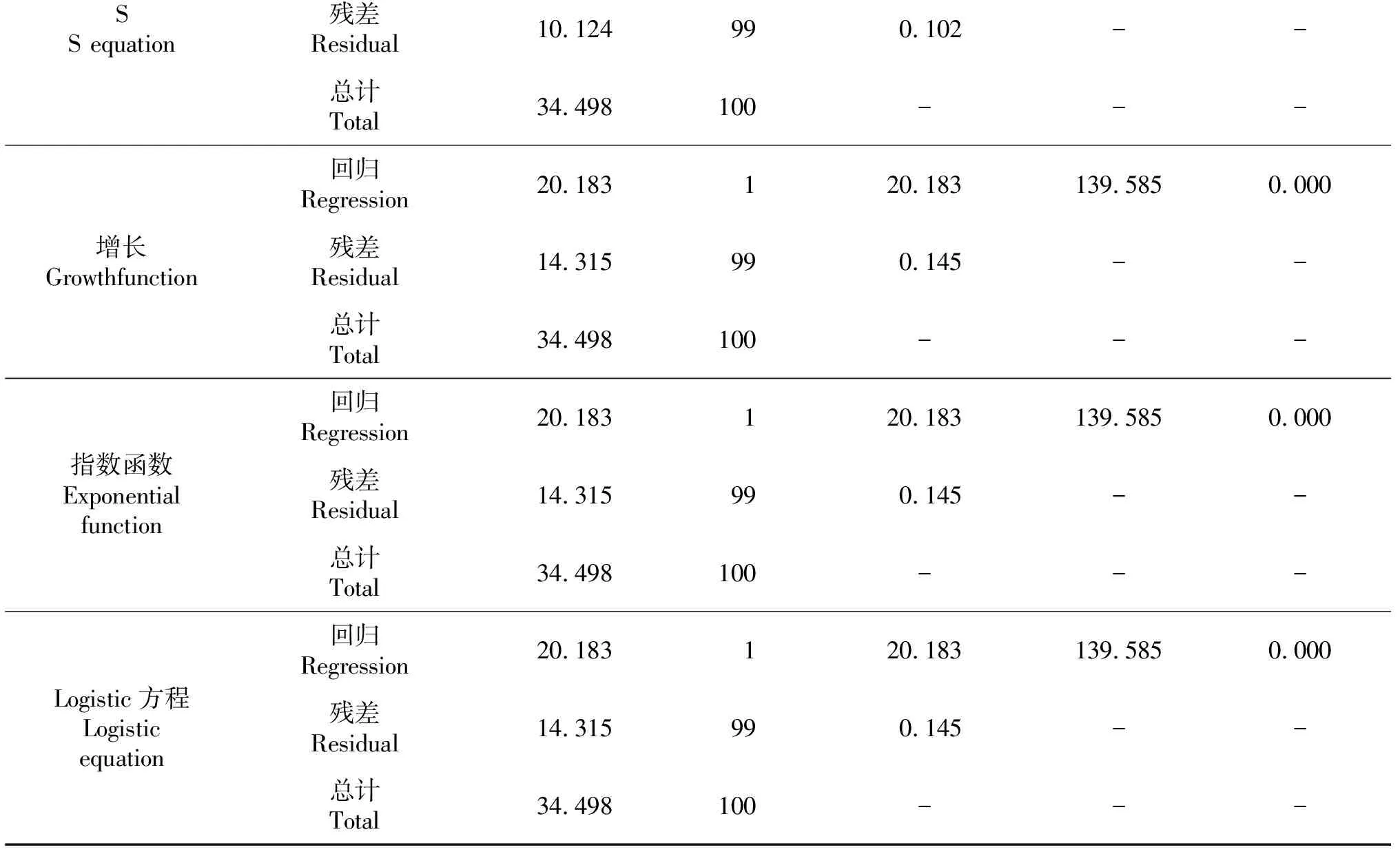
SS equation残差Residual10.124990.102--总计Total34.498100---回归Regression20.183120.183139.5850.000增长Growthfunction残差Residual14.315990.145--总计Total34.498100---回归Regression20.183120.183139.5850.000指数函数Exponential function残差Residual14.315990.145--总计Total34.498100---回归Regression20.183120.183139.5850.000Logistic方程Logistic equation残差Residual14.315990.145--总计Total34.498100---
3.4 米槁种群树高-胸径曲线拟合精度检验
通过米槁种群胸径、树高的实测数据以及采用11种模型对树高、胸径进行曲线拟合研究,结果发现这些模型形式都有一定的预测效果,其中拟合效果最好的是幂函数模型,其次是三次多项式函数模型和对数函数模型.通过对模型使用的可靠性进行检验[27],并将实测树高、胸径数据分别代入幂函数模型、三次多项式函数模型和对数函数模型这3个拟合较好的模型中,计算出树高、胸径的预测值,并进行T检验.并根据米槁种群树高胸径的幂函数模型H=2.255×D0.602得到反演树高值.得到结果如表5所示,可知米槁种群树高和胸径的实测值和预测值之间无显著性差异(P>0.05),由于幂函数模型、三次多项式函数模型和对数函数模型的决定系数R2值分别为为0.777、0.767、0.762,由此可见幂函数拟合模型的精度最高,且拟合精度明显大于三次多项式模型和对数模型,表明幂函数模型是米槁种群树高胸径的最佳拟合模型,可用来预测米槁种群的树高和胸径的值.
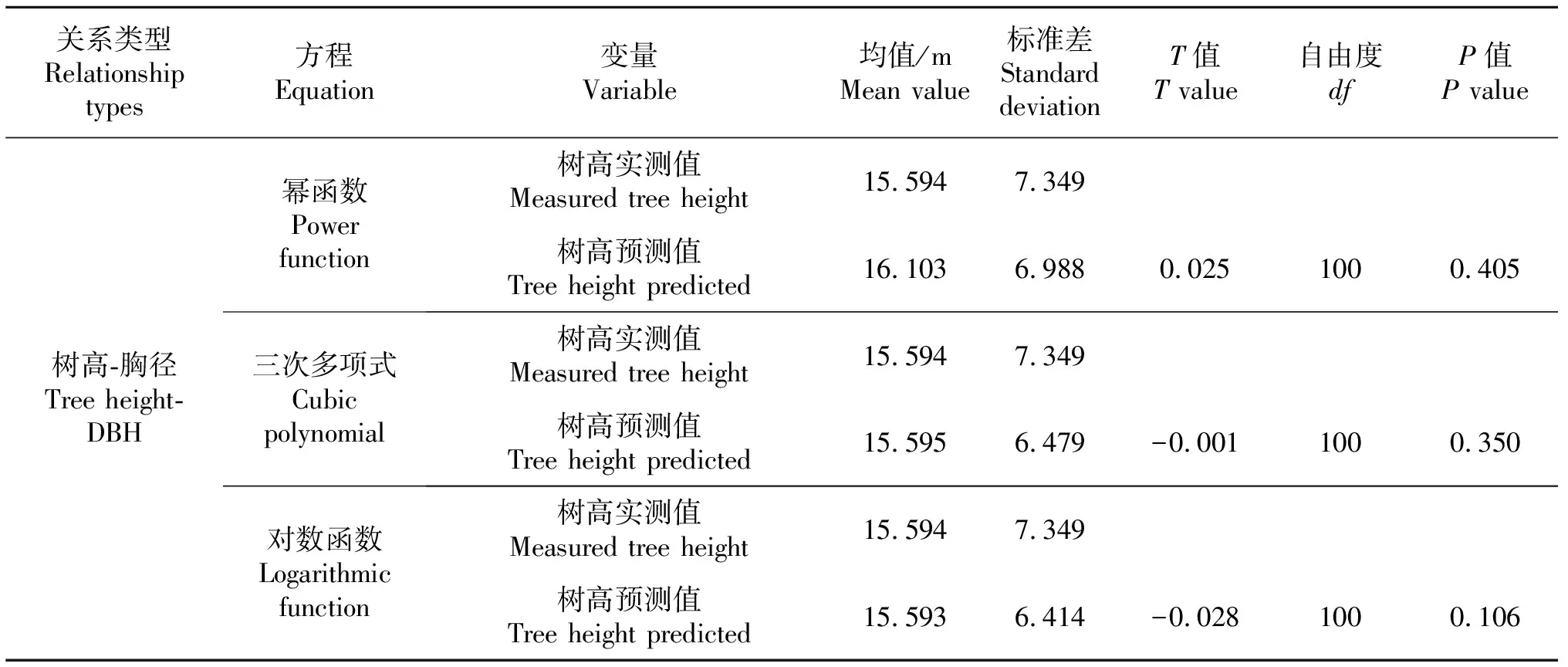
表5 米槁种群树高-胸径生长模型的检验
4 讨论
本研究采用空间代替时间方法,用米槁径级结构代替年龄结构,分析米槁种群树高、胸径的分布规律.并基于米槁种群树高、胸径的实测数据,选用11个曲线模型对树高-胸径进行拟合,根据模型的判定系数(R2)、模型曲线与散点综合分布图、回归模型的方差检验,以及T检验验证拟合精度,从中筛选出了拟合优度较高的幂函数模型为最优模型.
根据米槁种群胸径结构的特点,可知米槁种群胸径分布的总体波动范围随着胸径的增加,植株比例逐渐下降,趋势呈下降趋势,且小径木和中径木比例小,数量缺失严重.米槁种群树高分布整体出现2次明显的下降,米槁种群数量在0~12 m的树高范围内随着树高的增长而逐渐减少,之后增加,在12~32 m的树高范围内继续减少.这表明米槁种群退化,下降的原因是米槁种群在苗期和幼苗期成长为成熟林期过程中,经过强力环境筛,环境筛的构件成分是多方面的,可能是环境条件的改变或种内、种间竞争,使个体很难通过而大量死亡,难进入种群的更替层,在一定程度上限制了米槁种群的自然更新.造成这种数量差异的原因也可能是米槁幼苗本身具有一定的耐阴性,需光量增加;米槁林下萌条对幼苗幼树数量有一定补充作用,幼苗的缺失未显现.
通过拟合米槁种群的树高-胸径获得的最优模型是幂函数模型:
lnH=2.255×D0.602(R2=0.777)
通过对米槁种群树高-胸径模型的研究,得出其树高与胸径之间的相关性显著,不同模型的拟合可以取得良好的效果,通过它可以预测林木的生长,同时为实现森林资源的优化配置提供数据基础[28].有关树高与胸径的关系研究,涉及的针叶树种以杉木、马尾松、落叶松等为主,阔叶树种以栎类、杨树等为主[16,29],从这些对树高和胸径关系研究的拟合方程来看,两者成正相关关系,本研究对米槁树高-胸径的相关性分析结果与之一致.另外,研究珍贵用材树种观光木胸径与树高的关系,采用6种生长方程分别拟合观光木树高生长模型,确定观光木的最优生长模型为二次方程,拟合精度也较高,可实现观光木人工林林分树高的有效估测.
如图3所示,树高与胸径之间的相关性部分地偏离,原因可能是受地形条件的影响,地形控制着基本的生态因子[30],如光照、水分、温度、土壤养分等的分布[31].在海拔高处生长的米槁种群由于土壤贫瘠、水分少、土层较薄等原因,生长速度相对较慢.这表明不同地区相同树种的树高-胸径关系拟合结果存在差异.影响树高与胸径之间关系的因素有很多,比如天然林林分结构的复杂性、资源环境状况、植物适应环境的方式以及对资源的竞争等,都会造成树高-胸径关系变化的多样化[32].
如果将气候因子和立地条件等加入到树高-胸径关系曲线研究中,或许可以进一步提高模型的精确度和适用性.而且由于贵州米槁天然林分布较少,就本调查范围内米槁的分布数量有限,其实测数据都有一定误差;其次,米槁天然林种群的生长环境复杂,其形态可能受水分、养分、光照条件以及树种之间的竞争和自身生长规律等多种因子的控制.根据模型结果显示,虽然拟合精度较高,但由于采集数据有限,仍需研究具有良好通用性和精度的反演模型.
5 结论
通过分析米槁种群的分布规律,并建立米槁种群树高-胸径关系模型分析其相关性,可知米槁种群树高-胸径的相关性显著,并在统计范围内,树高随着胸径的增大而增加.对幂函数模型、三次多项式函数模型和对数函数模型这3个拟合较好的模型中,进行T检验,结果发现实测值和预测值差异不显著,尤其幂函数模型拟合效果最好,能够很好地拟合米槁种群树高-胸径关系,且数据拟合精度的指标值表明整体拟合效果理想且精度高.所选的最优模型可用来估算米槁的胸径、树高的值,从而提高模型预测能力.相同树种米槁用多种模型拟合,其结果不同,本研究用11种曲线模型来对米槁树高-胸径关系进行拟合,克服了单一模型建立生长曲线的不准确性[28],为该区域米槁天然林生长规律和预测林木蓄积量研究提供理论支撑,同时为米槁种群保护措施的制定和合理开发策略的探讨提供科学依据.
