基于TMD的钝角风嘴钢箱梁涡激振动控制研究
2019-11-19曾要争
曾要争, 喻 梅
(1.重庆市交通规划勘察设计院, 重庆 400000;2.重庆交通大学山区桥梁结构与材料教育部工程研究中心, 重庆 400000)
来流气流遇到钝体结构时会发生分离和再附进而产生漩涡的脱落,当漩涡脱落频率与结构振动频率一致时,结构就会发生涡激振动,它是一种具有自激和限幅双重性质的风致振动,大多发生在常见风速下[1]。目前世界上很多桥梁,如中国香港昂船洲大桥[2]、丹麦Great Belt East桥[3]、俄罗斯伏尔加河大桥等均出现过涡振现象。长时间的振动也会引起结构的疲劳破坏,同时涡激振动也会影响桥上行人的舒适度和行车安全[4],因此,进行桥梁结构涡振性能试验及抑振措施研究具有重要的工程借鉴意义。
涡振的抑制措施主要有结构措施、机械措施和气动措施三类[5]。结构措施不能从根源上解决涡激振动的问题。气动措施是通过改变桥梁主梁的气动外形进而优化主梁的涡振性能,但需要通过反复试验找出涡振的影响因素。机械措施则是通过布置调制阻尼器抑制结构振动。Fujino Y等[6]在1985年讨论了TMD抑制桥塔的驰振,较早地介绍了TMD在桥梁上的应用。顾明等[7]针对大跨度桥梁的抖振采用TMD进行控制,并提出了TMD的最优阻尼比等参数。陈艾荣等[8]在试验室完成了应用TMD对斜拉桥竖向抖振控制研究。气动优化方案基本上是通过风洞试验完成的[9],而TMD制振措施的部分参数可以通过程序计算得到,比如:最优阻尼比、减振率、自振频率等[10]。流线型钢箱梁截面接近流线型,常被应用于大跨度桥梁。实际中,由于各种因素的限制,存在风嘴短而钝的流线型钢箱梁断面,且考虑人行道栏杆、检修车轨道等作用后,会进一步弱化主梁的涡振性能。
本文以流线型钢箱梁悬索桥为背景,通过1∶50节段模型风洞试验研究其涡振性能,基于TMD抑振机理,分析了TMD的相关参数给出最优方案,对以后同类桥梁涡振控制有一定的指导和借鉴意义。
1 TMD振动控制机理
机械措施控制涡激共振主要包括TMD(被动振动控制),AMD(主动振动控制)和HMD(混合振动控制)。TMD(Tuned Mass Damper),意思为调谐质量阻尼器,也被称为谐波吸收器,是安装在结构上,以减少机械振动振幅的装置。其应用可预防结构振动引起行人的不适、损伤或失效。它们经常用于电力传输、汽车、桥梁和其他建筑物等。TMD的作用机理如图1,它由一个小质量M2通过刚度为K2的弹簧连接在弹簧刚度为Ke的主结构质量Me。在简谐荷载f(t)的作用下,小质量M2可以通过自身的振动来吸收能量,从而减小主结构质量Me的振动,这样的结构极大增加了阻尼。
(1)


图1 主结构-TMD模型
由于涡激振动时桥梁受到了类似谐和激励,故在计算过程中把f(t)假设为谐和激励。
令f(t)=Peiωt,x1=A1eiωt,x2=A2eiωt,有:
(2)
式中:H(ω)=G-1(ω);G(ω)=[k-mω2+icω]。

(3)
H(ω)=ke-meω2+ic1ω
(4)
TMD参数包括阻尼器与结构的广义质量之比、频率之比及阻尼比,其参数的选取对制振效果至关重要。
对于调谐式阻尼器的频率之比、阻尼比可以按照下面公式计算:
(5)
(6)
式中:ω0为阻尼器的圆频率;ζ0为阻尼比;ωs为受控振型圆频率。
μ为阻尼器与结构受控振型的广义质量比,按下式计算:
(7)
式中:L为桥梁跨长或塔高;m0为阻尼器质量;m(x)为桥梁单位长度质量(kg/m);Φi(x)为受控振型值;x0为阻尼器安装位置;Φi(x0)为阻尼器按照位置相应于Φi(x)的振型值。
2 流线型钢箱主梁涡振控制
某主跨410 m的单主缆悬索桥,桥塔采用混凝土结构,主梁采用流线型钢箱梁。桥宽36.4 m,高3.5 m,主梁宽高比为10.4,风嘴截面夹角为79.6 °,风嘴宽0.6 m,风嘴短而钝(图2)。桥梁结构的主要振型以及对应的频率见表1。

表1 桥梁动力特性

图2 主梁断面(单位:m)
2.1 节段试验模型试验及结果
为研究该桥的涡振性能,制作主梁的节段模型进行风洞试验。节段模型的几何缩尺比为1∶50,模型长2.095 m,宽0.728 m,高0.070 m,且风洞试验阻塞比小于5 %。模型采用优质木材和塑料板制作,人行道栏杆等附属构件均采用高级塑料板由数控雕刻机制作而成。试验在均匀流场中进行,节段模型由8根拉伸弹簧悬挂在支架上,且模型两端设置端板(图3),相关试验参数见表2。根据JTG/T D60-01-2004《公路桥梁抗风设计规范》的有关规定,按一阶对称竖弯计算的涡振振幅允许值为:0.1386 m。

图3 节段模型
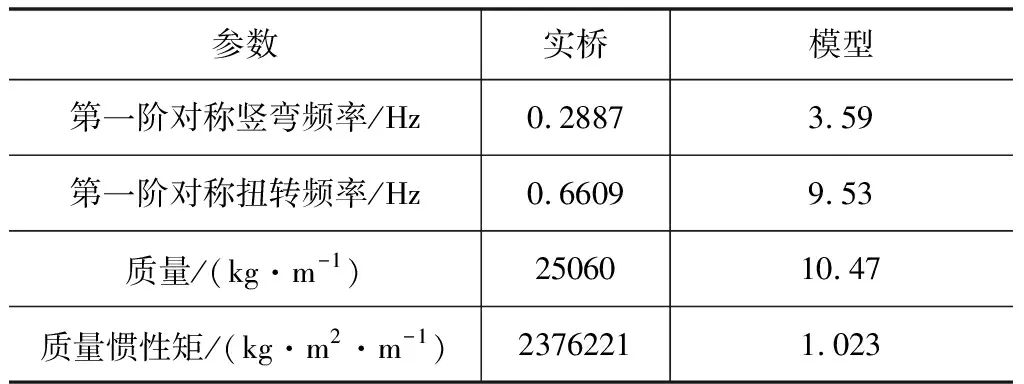
参数实桥模型第一阶对称竖弯频率/Hz0.28873.59第一阶对称扭转频率/Hz0.66099.53质量/(kg·m-1)2506010.47质量惯性矩/(kg·m2·m-1)23762211.023
本文主要分析阻尼比为0.3 %,攻角为±5 °、±3 °和0 °时主梁的涡振性能。
成桥状态下,主梁在-5 °、-3 °攻角时,未出现明显的涡激振动(未列出数据)。如图4,0 °攻角时,主梁出现了1个竖向涡振区;+3 °攻角时,主梁出现了2个竖向涡振区,其中第2个竖向涡振区的主梁竖向最大振幅为438 mm,远大于规范允许值。+5 °攻角时,出现了2个竖向涡振区,其中,最大涡振振幅对应的风速均在30 m/s左右,与该桥主梁设计基准风速30.1 m/s较接近。因此,本文重点关注风速小于主梁高度处设计基准风速时主梁的涡振性能,即攻角3 °和0 °时的主梁涡振性能。

图4 主梁断面竖向涡振响应
2.2 TMD振动控制与参数分析
为了取得最大减振率,TMD一般布置在振型最大处。TMD质量,在桥跨范围内按两个截面布置,每个截面分成一个到两个箱布置,对于第一阶竖向振型布置1处,每处Mt,M/2×2(每处两个箱各1)×1(处)=Mt。对于M和T的取值见表3。
试验时考虑实桥阻尼比为0.1 %、0.3 %、0.5 %和0.8 %。行程比为安装TMD后的桥梁振动振幅与TMD的振动振幅的比值;减振率为安装TMD后,与未装TMD相比振动振幅的减小的比例。TMD的质量分别取为10 t、30 t、40 t、50 t、60 t、70 t和80 t情况;另外还考虑一些特殊情况,比如质量比为0.4 %和0.5 %的情况。

表3 TMD不同质量时的最优参数
图5、图6给出了不同质量比时的行程比和减振比结果,可知,TMD的阻尼比对制振效果影响显著,取最优阻尼比时效果最好,阻尼比为15 %时效果最差。但TMD取最优阻尼比行程过大,不利于TMD在工程中的应用。尽管10 %的阻尼比比最优阻尼比制振效果有所减弱,但仍然满足要求,且TMD的行程始终;阻尼比大于15 %时,制振效率下降。综合考虑,TMD取10 %左右最为合适。
对于第一阶竖向振型,尽管这一振型的TMD的总质量为10 t时,便可以符合要求,但为了安全,建议取20 t。表4给出了具体的TMD参数,表5给出了对应的制振结果,从中可以看出TMD制振效果良好,采用TMD制振方案后,主梁涡振振幅满足中国规范允许值。

图5 TMD阻尼比对行程比的影响

表4 主梁TMD控制参数建议

表5 TMD制振方案对于主梁竖向涡振的抑制效果
2.3 舒适度评价
对于舒适度只需考虑风速小于10 m/s时发生的涡激共振,因此主要考虑竖向迪克曼指标的K值和杰奈威指标[11]对舒适度进行评价,其具体定义见文献[11]。
表6和表7对比了原设计方案和TMD制振方案。对于原方案,主梁会出现很大的涡激共振,使行人非常不舒服,并且感觉疲劳,难以忍受。而加TMD后因为主梁涡激共振带来的不适感明显减少。因此,TMD措施可以抑制涡振,并且满足行人舒适度的要求。
其中,疲劳:一般人对振动过分疲劳的上限;短期忍:能忍受短期振动。
3 结论
通过节段模型风洞试验对带有短而钝风嘴的流线型钢箱梁的涡振性能进行了测试,提出采用TMD制振方案抑制主梁的竖向涡振,得出如下结论:

(a)主梁阻尼比0.1%

(b)主梁阻尼比0.3%
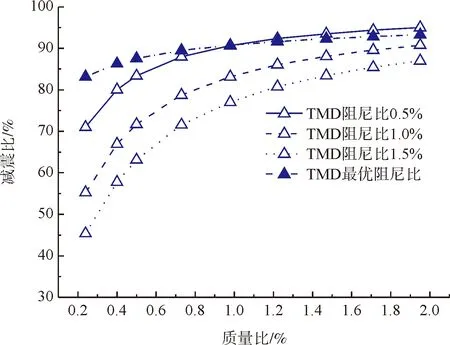
(c)主梁阻尼比0.5%

(d)主梁阻尼比0.8%

风攻角竖向频率/Hz原设计方案机械控制方案(TMD)最大位移/mmK值迪克曼指标最大位移/mmK值迪克曼指标0°0.288793.2515.5疲劳17.853.0短期忍3°0.288712821.3疲劳24.504.08短期忍

表7 优化与不优化的舒适度(杰奈威指标VG)
(1)流线型钢主梁在0 °、+3 °及+5 °攻角下出现了明显的竖向涡激振动,且最大振幅大于中国规范允许值;但重点关注风速小于主梁高度处设计基准风速时主梁的涡振性能,即风攻角3 °和0 °时的主梁涡振性能。
(2)针对主梁的竖向涡激共振振幅大于容许值,研究了TMD制振方案来抑制涡激共振,抑制效果良好。
(3)利用迪克曼指标和杰奈威指标评价了原方案和加TMD后主梁的舒适度,表明TMD制振方案不仅可以抑制主梁竖向涡振同时可以满足舒适度要求。
