起重机n阶伸缩臂架稳定性的递推公式及数值解法

姚峰林 孟文俊 赵 婕 张志德 申昌宏 闫俊慧 刘海波

1.太原科技大学机械工程学院，太原，030024 2.太原大学计算机工程系，太原，0300323.太原重工股份有限公司工程机械分公司，太原，030024

0 引言

近年来，随着高强度钢材的大量使用和自动单缸插销技术的成熟，多节伸缩臂架技术广泛应用到大型工程起重机上。随着钢结构高度的不断增大，钢材的消耗量也在不断增加，梁柱的截面沿轴向发生变化是一种经济型承担载荷的方式。箱形阶梯柱模型以其长度易于伸缩变化，承载力大和材料利用率高等优点,广泛用于工程起重机、高空救援车等各类机械设备中，其稳定性为学者研究的重点[1-2]。TIMOSHENKO等[3]对阶梯柱模型进行了研究和分析，并使用能量法对高阶阶梯柱的临界力进行了计算。王欣等[4]借助预设近似挠度曲线，使用能量法和李兹法对阶梯柱进行了研究，但该方法相当于引入了附加约束，特别是对于四阶以上的阶梯柱会产生较大的误差。文献[5-7]使用传递矩阵法对阶梯柱的临界力进行了研究，但该方法目前也只能用于阶数较少的阶梯柱，在阶梯柱阶数较大情况下使用该方法也会出现较大的误差。随着有限元理论的发展和完善，陆念力等[8-10]使用精确有限元法对阶梯柱的临界力进行了研究。

我国现行的国家标准GB/T3811—2008[11]将文献[8-10]的方法作为规范的阶梯柱稳定性分析精确计算方法，但这种方法对于多阶阶梯柱来说，其刚度矩阵相当庞大，特征方程复杂，对于常见支撑形式的阶梯柱稳定性精确数值解，常通过试凑法获得，计算量巨大，给实际应用带来了一定的困难。在现行的设计规范中，使用图表来表示2～5阶的阶梯柱部分特殊组合情况下的长度系数，但当阶数超过5阶时便无法应用，并且在非特定组合时使用线性拟合的方法，没有给出线性拟合的误差。德国Liebherr LTM 11200、徐工集团QAY1200、三一重工的SANY SAC12000、中联重科的QAY2000等机型的伸缩臂架阶数都达到了8，此时现有的规范就无法满足实际工程的需要,因此需要一种方法，可以较方便且迅速地求解5阶及以上阶梯柱临界力的方法。本文基于纵横弯曲理论建立了n阶伸缩臂阶梯柱的微分方程组，并利用数学归纳法推导出n阶阶梯柱压杆稳定性的递推公式。

1 阶梯柱结构变形及其微分方程

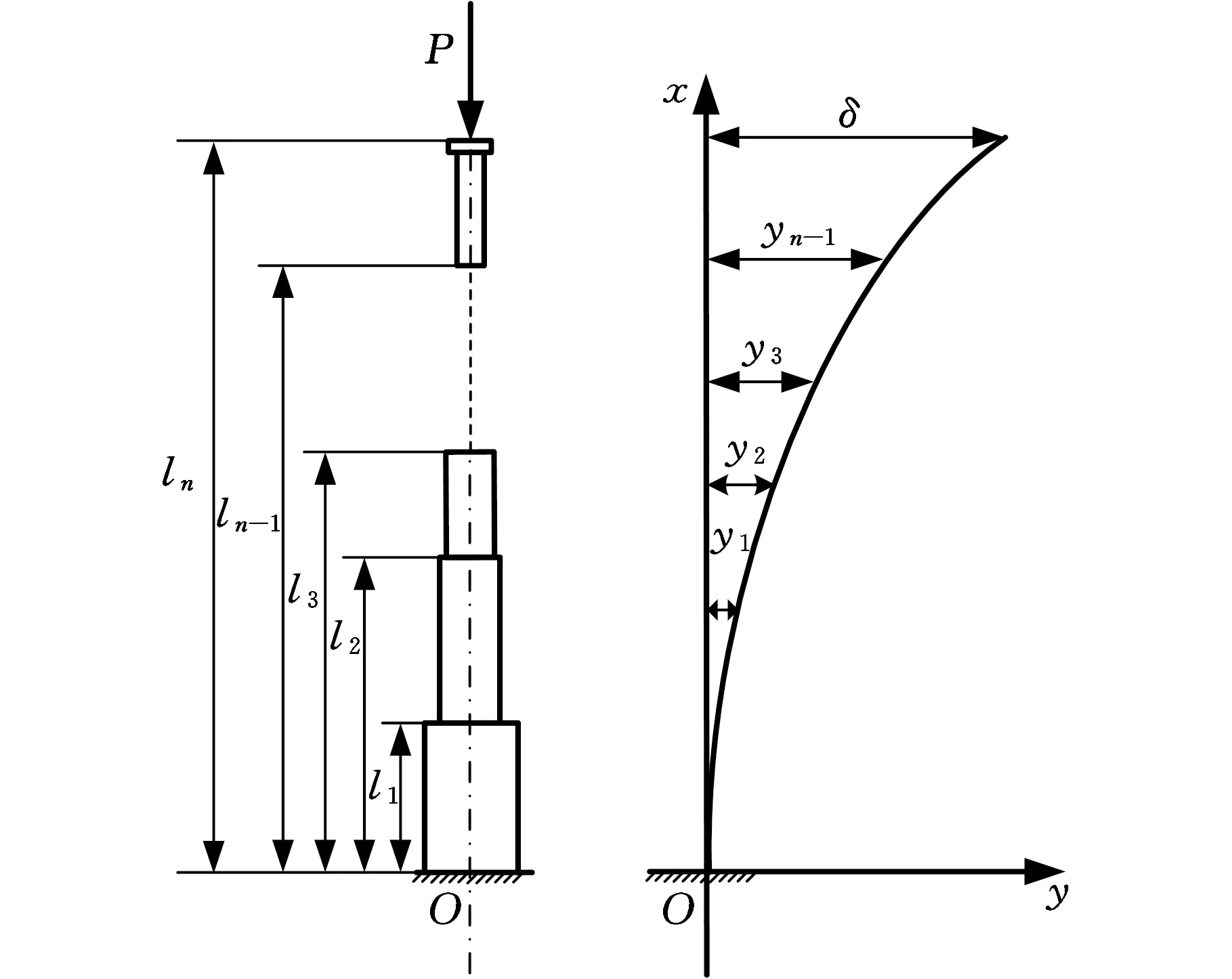
图1 变截面阶梯柱模型及受力简图 Fig.1 Mechanical model and force diagram of a multi-stepped column

针对n阶阶梯柱模型，基于纵横弯曲理论可建立各节伸缩臂挠曲微分方程。如图1所示，n阶阶梯柱的总长为ln，P为伸缩臂顶端承受的轴向力且P的方向保持不变，δ为伸缩臂顶端的侧向位移。假设轴向力和弯矩全部由伸缩臂承受[12-13]，那么第i阶压杆模型的受力和变形如图2所示。

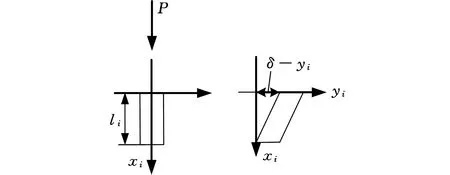
图2 第i阶压杆模型受力及位移图Fig.2 Force and displacement diagram of thei-th section

根据模型可列出以下方程：

(1)

i=1,2,…,n

式中，Ii为第i节伸缩臂的截面惯性矩，m4；li为第i节伸缩臂顶部到吊臂根部的长度，m；yi为第i节伸缩臂在平面内偏离x轴的侧向位移，m；y″2为yi的二阶导数；E为弹性模量，Pa。

式(1)可统一表示为

(2)

(3)

式(2)的通解为

yi=Aisinkix+Bicoskix+δ

(4)

由挠度位移边界条件可解出各积分常数之间的关系为

(5)

A1=0B1=-δ

(6)

(7)

(8)

记

(9)

可得到未知系数An和Bn的表达式

(10)

由伸缩臂顶部边界条件:x=ln时yn=δ，得

Ansinknln+Bncosknln=0

(11)

将式(10)代入式(11)中得到伸缩臂失稳特征方程为

(12)

对于一个特定起重机箱形伸缩臂，将所有已知条件代入失稳特征方程可知，式(12)是以P为未知量的非线性方程，即失稳特征方程为超越方程，解此非线性方程即可求得结构失稳临界力P。

2 超越方程的递推规律

当n=1时，根据式(12)可以得到

cosk1l1=0

(13)

当n=2时，可以得到

(14)

当n=3时，可以得到

(15)

根据数学归纳法，可以证明n阶阶梯柱的失稳特征方程如下：

sinknlnC(n)+cosknlnD(n)=0

(16)

C(n)=(sinkn-1ln-1sinknln-1+

(coskn-1ln-1sinknln-1-

(17)

D(n)=(coskn-1ln-1cosknln-1+

(sinkn-1ln-1cosknln-1-

(18)

D(1)=1C(1)=0

(19)

3 超越方程的数值解法

3.1 超越方程的非线性特征

已知某二阶阶梯柱,l1=15.4 m，l2=29.9 m，I1=43.26×10-3m4，I2=26.09×10-3m4，利用式(14)可以得到二阶阶梯柱所构成函数的曲线如图3所示。此函数是一非线性函数且不具有规则的周期性，满足失稳特征方程f(k1,k2)=0的点较多,所以必须通过增加方程的方法来确定临界点。将式(3)进行变形可得增加的方程如下:

(20)

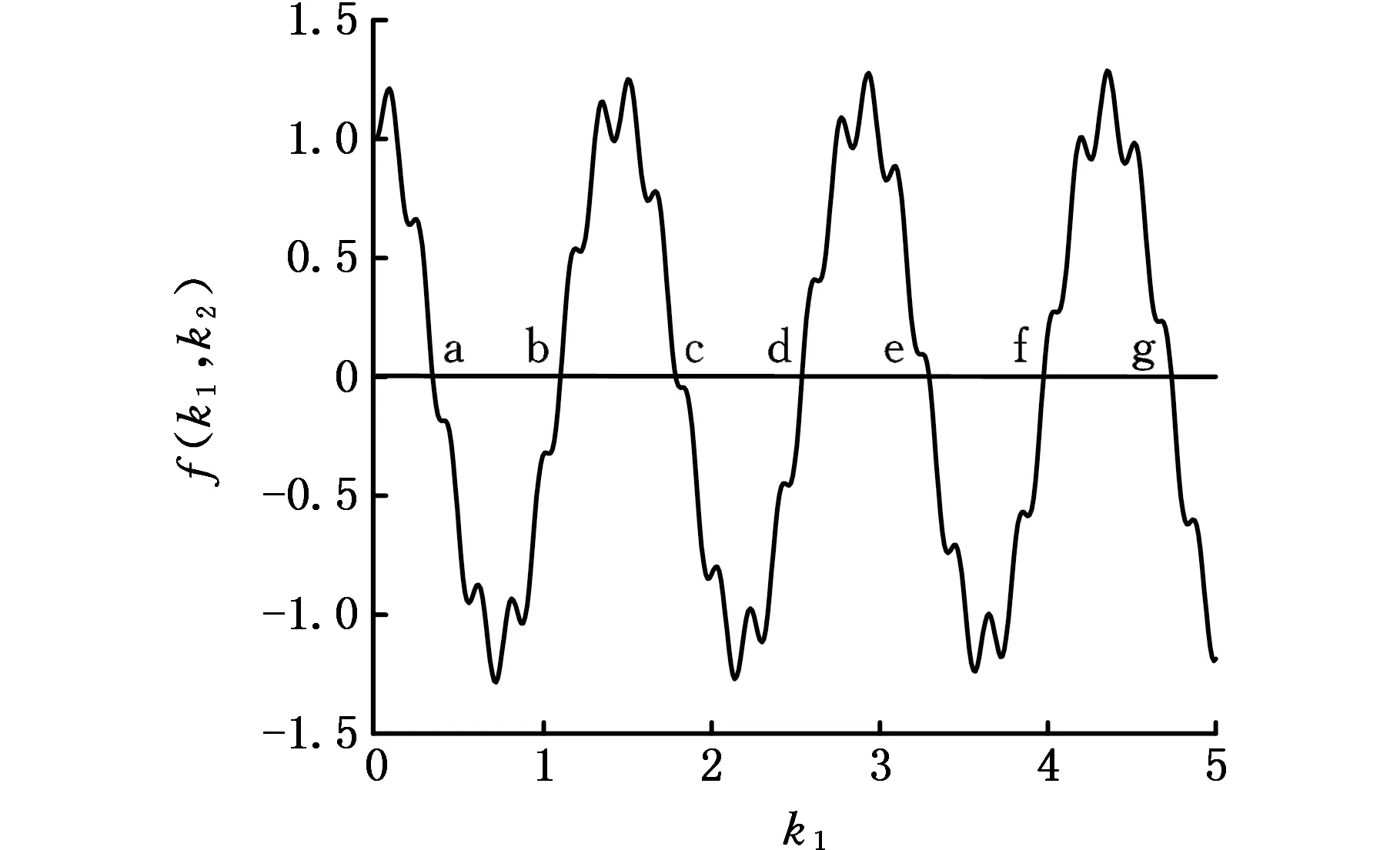
图3 二阶阶梯柱的特征方程多项式与k1函数关系Fig.3 Relationship between k1 and buckin g characteristic equation of the stepped column wit h two sections

对于此二阶阶梯柱，数值求解方程组为

数值求解结果如下：k1=0.048 0，k2=0.061 7；得到临界力P=2.049 1×107N，长度系数μ2=1.060 12。

3.2 n阶超越方程组的非线性数值解法

当阶梯柱的阶数为n时，超越方程组可以通过增加其约束限制方程建立方程组来求解。所建立的n阶超越方程组如下：

(21)

到目前为止，这种非线性超越方程还不存在解析解，只有数值解。数值解常使用的方法包括欧拉法、龙格库塔法、Gauss-Newton法[14]等，但这些方法可能由于矩阵的奇异而无解。本文使用Levenberg-Marquardt算法[14]来进行求解,这种算法具有梯度法和牛顿法的优点并较原来的梯度下降法求解速度提高了几十倍甚至上百倍，并且由式(21)所构建的方程组总能得到最优数值解。

通过式(21)可以求解出每节阶梯柱的刚度，进而可以求出整个阶梯柱模型的临界力P，此临界力与相同约束条件下与阶梯柱长度相等的基本臂截面所构成均等截面柱的临界力对比，就可以求出n阶阶梯柱的长度系数μ2。计算公式如下：

(22)

3.3 二阶阶梯柱的非线性及其插值

由图4可以看出，使用本文数值方法计算的二阶阶梯柱长度系数与使用ANSYS 17.0计算出的长度系数差值非常小，最大相对误差为1.7×10-4，由此可知n阶压杆稳定性计算的递推公式精度较高。此外，随着第二阶柱的惯性矩的增大，长度系数μ2减小，即阶梯柱的临界力逐渐增大；随着第一阶臂架长度l1与全长臂架长度l之比α1增大即第二阶柱的相对长度减小，长度系数μ2非线性减小。因此在使用GB/T3811—2008中的方法查表得到μ2值时，如果选用了表中没有的βi，那么需使用数值法进行线性插值才可以得到更为准确的结果；另外α1也会影响最终的长度系数值。

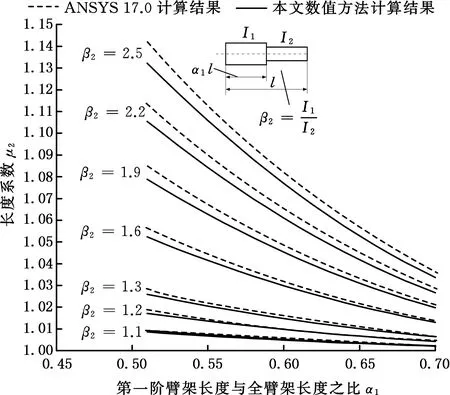
图4 二阶阶梯柱的长度系数μ2值Fig.4 Length coefficient μ2 of stepped colum n with two sections

3.4 多阶阶梯柱的长度系数

表1～表3所示为不同方法计算的三阶、四阶、五阶阶梯柱长度系数μ2的比较。使用数值法对某8阶阶梯柱进行临界力计算，其参数和结果如表4所示。最终可以得到临界力P=1.3049×106N ,长度系数μ2=2.680。

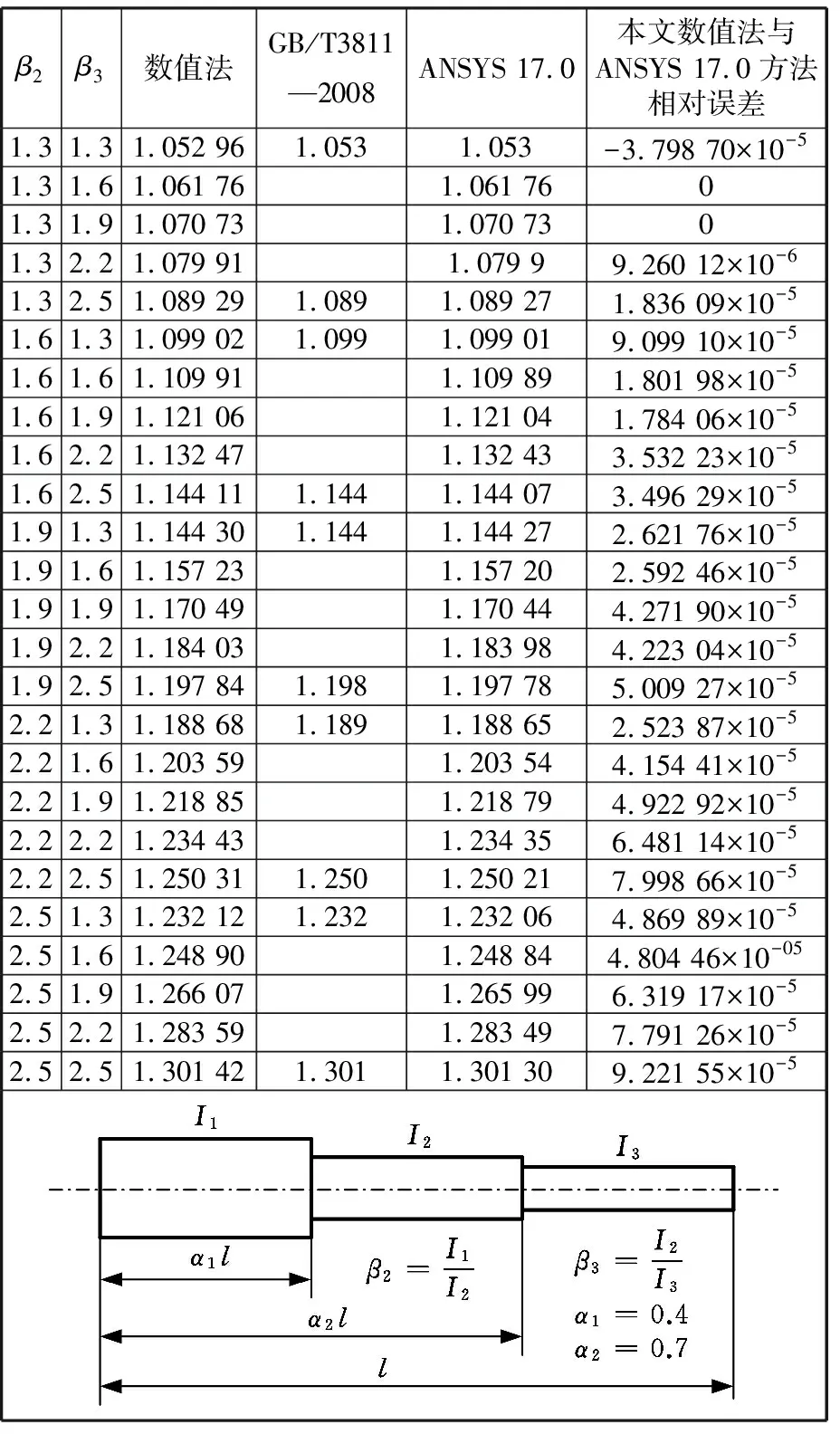
表1 三阶阶梯柱计算长度系数及比较

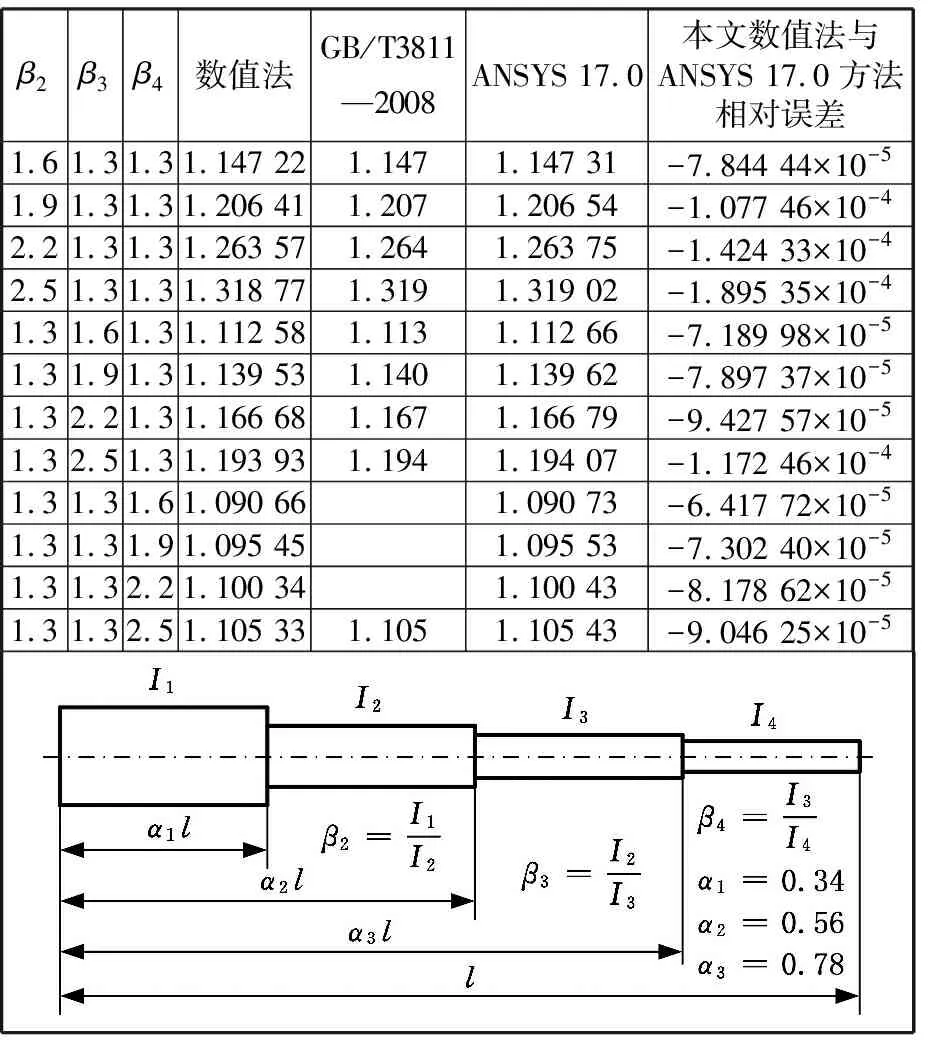
表2 四阶阶梯柱计算长度系数及比较

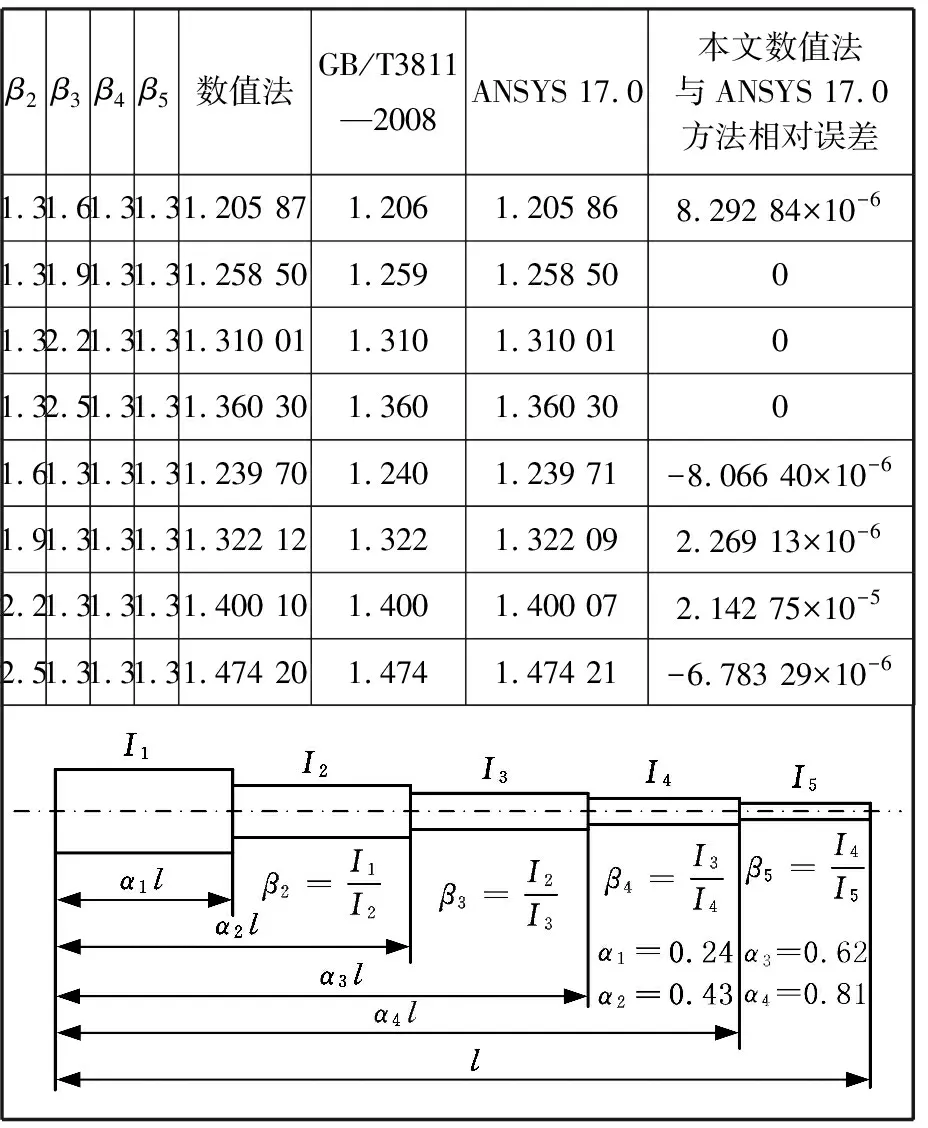
表3 五阶阶梯柱计算长度系数及比较

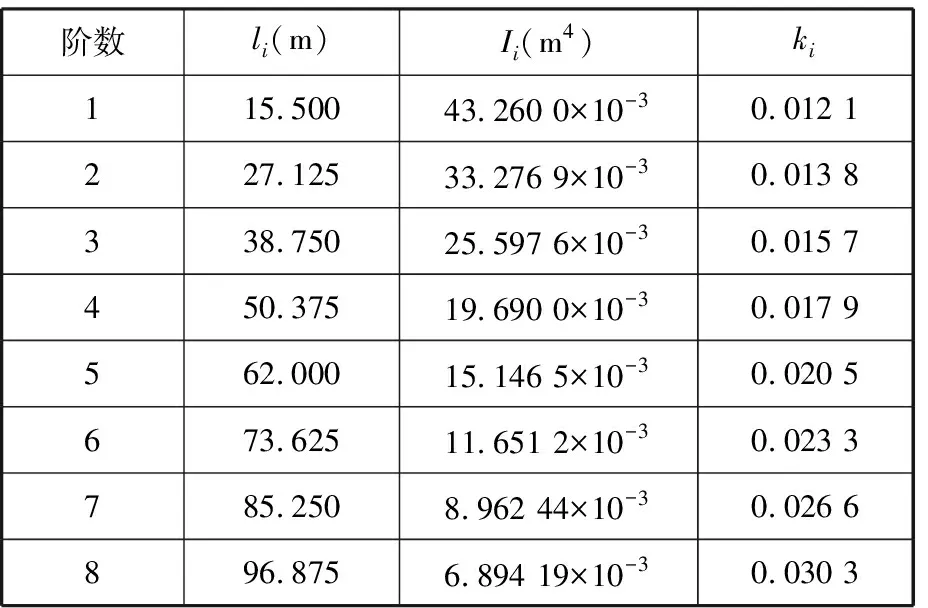
表4 某八阶阶梯柱临界力计算参数及结果

八阶阶梯柱计算长度系数及比较见表5，其中μ为由多级阶梯柱侧向刚度分析实用算式得到的计算长度系数[11],μa为使用精确有限元法得到的等效构件的计算长度系数[9]，Me为使用等效构件法得到的计算长度系数[11]。

上文分别给出三阶、四阶、五阶、八阶阶梯柱的长度系数的数值计算结果，并且使用ANSYS 17.0对上述阶梯柱的组合进行了求解，并对本文递推公式得到的结果与ANSYS 17.0计算结果进行了对比，发现该递推公式与Levenberg-Marquardt算法相结合所求解出的长度系数具有很高的精度。

使用MATLAB2014b编制了n阶超越方程组的非线性数值解程序,该程序可以对9阶及9阶以下，长度和惯性矩任意组合的阶梯柱的临界应力和长度系数进行求解。

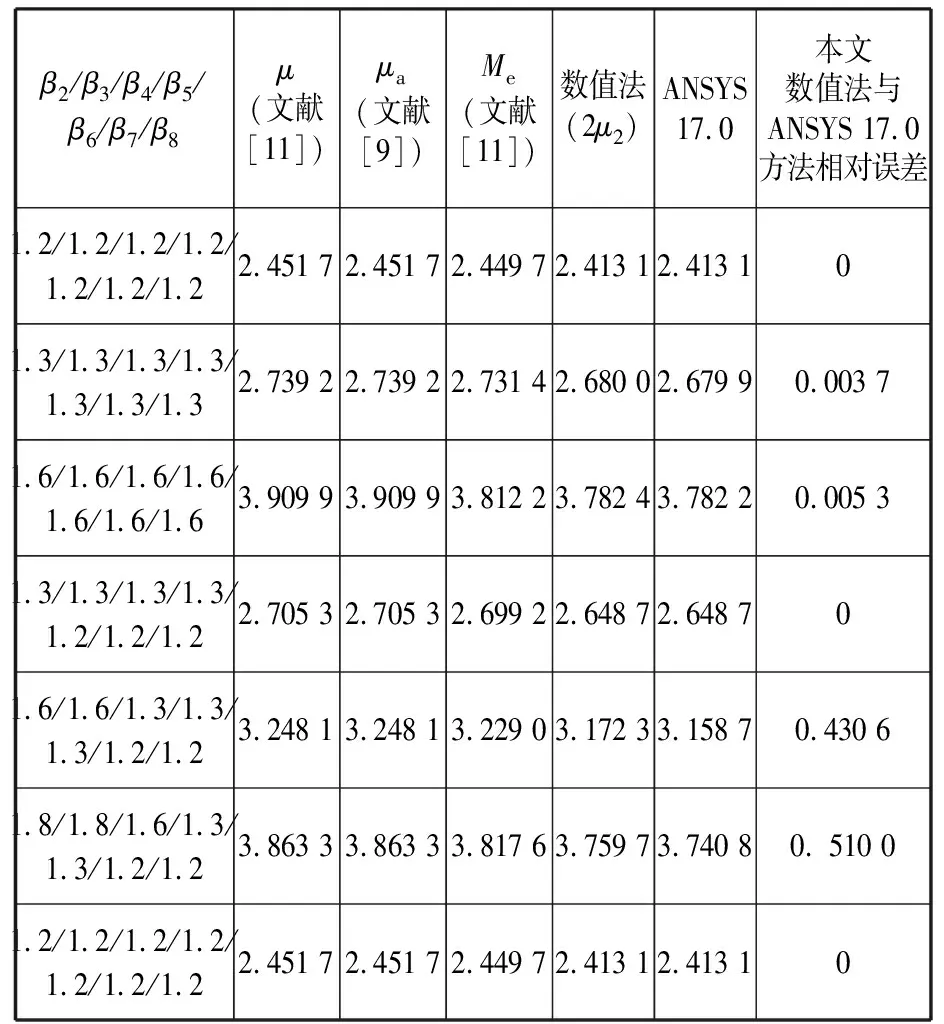
表5 八阶阶梯柱计算长度系数及比较

4 结论

本文使用伸缩臂的阶梯柱模型对n阶阶梯柱的稳定性微分方程组进行了推导，得到了n阶阶梯柱递推公式，根据阶梯柱模型的力学和结构特性，列写了补充方程；使用Levenberg-Marquardt数值算法求解n阶阶梯柱的超越方程组，与现行国家标准GB/T3811—2008和ANSYS 17.0所得结果进行对比，结果证明了n阶阶梯柱递推公式正确，数值解法相比其他的计算方法通用性更强，精度更高。此外，阶梯柱模型的长度系数具有一定的非线性，小范围内的插值不会产生太大的误差，但对于大截面的阶梯柱模型，若使用插值法计算，则临界力的误差较大。