基于核心素养建构速度和加速度概念的案例选择与设计

邵泽义　秦晓文

摘 要：本文针对速度和加速度的概念建构难点，提出了以百米赛跑为关键案例支持学生建构速度和加速度，并对这一关键案例进行了分析和设计，以引导学生基于实际问题，在对运动描述的不断细化过程中，逐级建构速度和加速度的概念.

关键词：案例选择;关键案例;速度;加速度

文章编号：1008-4134（2019）19-0008中图分类号：G633.7文献标识码：B

基金项目：北京市教育科学“十三五”规划课题“基于核心素养的科学教学问题梳理与解决方案研究”（课题编号：CDDB18158）.

作者简介：邵泽义（1963-），男，吉林人，硕士，北京教育科学研究院物理教研员;

秦晓文（1968-），男，山东人，硕士，北京市特级教师，北京教育科学研究院物理教研员.

速度和加速度是高中物理中的核心概念，如何帮助学生建构瞬时速度和加速度概念，一直是高中物理教学的重点，也是难点.尽管速度和加速度概念教学的研究案例很多，也取得了很多有效的成果，但少有基于学生个体体验、自主建构的研究.究其原因是缺乏关键案例，缺乏和学生个体经验相符合的并能够积极参与其中的案例.针对这一问题，本文将介绍笔者实践探索的经验，供读者借鉴.

1 关键案例的选择

能支持学生体验并自主建构概念的关键案例应符合如下几点：（1）是学生常见或熟悉的实际问题，能将学生的生活经验和科学概念联系起来，可以分层次开展探究;（2）可以激发学生探究欲望;（3）案例中蕴涵着能引发学生科学思维的问题情境，可以挖掘出不同层次的探究任务.

笔者在实践探索中逐渐体会到，百米赛跑可以作为关键案例，从对世界冠军博尔特的百米赛跑研究，到学生自己百米赛跑的实践，学生在对运动描述不断细化的过程中，可以逐步建构出速度和加速度的概念.

世界冠军博尔特的百米赛跑是学生熟知的一个真实案例，虽然学生大都参加过百米赛跑，但是很少有机会描述自己百米赛跑的运动过程.本案例的引入，可以使学生体会研究及描述运动的基本方法，通过有关资料感受百年来世界百米赛跑纪录的提高过程，并产生浓厚的研究兴趣.

在奥运会上，百米赛跑最能吸引人们的目光，获得百米跑奥运会冠军的人通常被称为“世界上跑的最快的人”.迄今为止此人仍然是牙买加的博尔特，他在2009年8月19日柏林世锦赛男子100米决赛中，以9.58秒夺冠，并保持记录至今.体育运动专家一直在研究怎样才能创造新的世界纪录，通过网络查询，能够获得百米赛跑世界记录的数据，据此绘制出图1，从图象可以看出，近五十年里世界纪录的变化不超过0.5秒，可见打破纪录是非常艰难的.

2 关键案例的分析与设计

运动专家研究怎样提高成绩打破世界纪录，首先就要研究这些记录的创造者是怎样跑的：运动员起跑后是一直加速跑到終点？还是加速跑到一定阶段后匀速跑到终点？还是先加速、后匀速、最后再加速？最大奔跑速度出现在什么阶段？运动员一共迈出多少步？每一步多长（步长）？每秒钟迈出多少步（步频）？为了搞清楚这些问题，就要对运动员的跑步过程进行测量以获得数据，然后对数据进行分析.

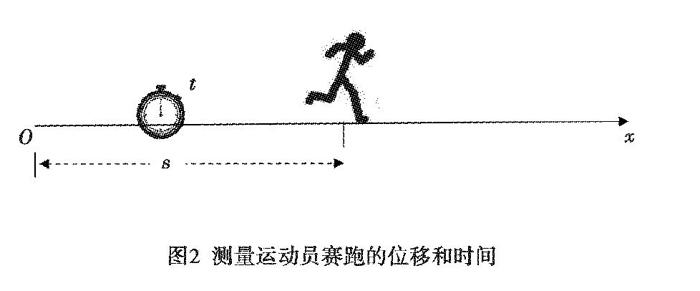
如图2，一个最基本的测量就是确定某一时刻运动员跑到了什么位置，也就是测量运动员离开起跑点的位移和所用时间，取得一组s-t数据.测量物体的运动时间和位移，是研究运动的最基本方法.

对博尔特百米赛跑进行的最粗略的描述，就是根据最终测量数据，计算百米全程的平均速度.当他完成100米冲刺时，离开起点的位移是100米，测得运动时间是9.58秒.那么他全程的平均速度就是：

v=s/t =100/9.58m/s=10.44m/s

这个速度的含义是：假设博尔特在这100米的路程里保持匀速运动，那么速度就是10.44m/s，用图象表示的百米运动过程如图3所示，这是学生在初中就掌握的描述运动方法：s-t图象是直线，代表匀速直线运动，v-t图象平行时间轴，也代表匀速直线运动.

很显然，博尔特的百米跑有起步加速阶段，把全程作为匀速运动是很粗略的运动描述，原因是测量数据太少，只有100米位移和对应的时间9.58秒两个数据.怎样才能对全程运动进行精确的描述呢？只有多测量取得较多的数据.一个想法是每隔10米测量一次时间，这样就可以得到一组10个位移数据和对应的10个时间数据.让学生们设想一下，可以采用什么方法进行测量，以获得一组共20个数据.

表1就是博尔特在奔跑过程中位移每增加10米记录一次时间的数据表.可以设想在百米跑道旁每隔10米站一位手持计时器的计时员，一共需要10个人计时，当起跑发令枪打响后，10人同时启动计时器，当博尔特跑到10米位置时，第一位计时员停止计时，跑到20米位置时，第二位计时员停止计时……以此类推，就得到10个时间记录.可以让学生思考一下这种测量方法是否可行.

根据表1，可以绘制位移—时间图象，也就是s-t图象，如图4.以运动时间为横坐标，以运动距离为纵坐标，起跑点为原点，确定坐标轴适合的刻度，用表格中的数据描出10个点，再用平滑的曲线把这些点连接起来，就绘制出s-t图象.

观察图象，可以看出起跑后的最初3秒，描述运动的图线是弯曲的，3秒后图象变成直线，表示奔跑距离随着时间均匀增加.s-t图象中的直线显示位移随着时间均匀变化，表示的是匀速直线运动.因此在第3秒到接近10秒这段时间里，博尔特是匀速运动的，可以根据图象计算速度.

v=Δs/Δt=100-20/9.6-2.9=11.94m/s

这显然比全程的平均速度10.44m/s要大.根据位移图象可以做出这样的运动描述：博尔特在起步后的前3秒内加速运动，第3秒末速度达到约12米/秒，之后匀速运动到终点.据此可以绘出博尔特跑步的速度图象如图5所示.

博尔特在起跑阶段用3秒钟把速度从零提高到12米/秒，也就是在运动的起始3秒内，速度的变化量 Δv=12-0=12m/s，因此每秒钟增加的速度为：

a=Δv/Δt=4m/s2

这个比值是“单位时间内速度的变化”，我们称之为加速度，用符号a表示，加速度数值越大，表明提速本领越强.这个比值也称为这段图象的斜率.这样我们对博尔特的百米赛跑就有了进一步的描述：博尔特在起跑后的3秒内做加速运动，加速度为4m/s2，当速度达到12m/s后，开始做匀速运动并一直保持到终点.很显然，这种运动描述比把百米全程看成匀速运动更符合实际，更加精确.而且找出了能够描述提速能力的物理量——加速度.

有人会问，百米冲刺时怎么不是加速呢？看来对百米运动的描述还需要细化，要进行分段研究，来观察每个10米位移内的速度变化.根据数据表2，把一百米分成10米一段，计算出每段所用的时间和每段的平均速度，得到数据表2.

从表2可以看出，每段的平均速度是变化的，最大速度出现在第7段，达到12.35m/s，这说明把运动的前3秒看成加速运动，后7秒看成匀速运动的描述还是比较粗略.为了显示博尔特的速度随时间的变化，根据表2得到数据表3.

根据表3，绘制出博尔特百米跑速度图，如图6所示.根据10个描点，绘制速度变化的趋势线，图象显示全程运动的前7秒是加速过程，后3秒是减速过程，冲刺阶段并没有加速反而减速，说明人的体力有衰减.

根据图6，我们可以把百米赛跑看成三个过程;很快的加速、缓慢的加速和略微的减速，并计算出每段的加速度.

0—3秒，a=Δv/Δt=10-3/3-0=3.33m/s2

3—7秒，a=Δv/Δt=12.35-10/7-3=0.59m/s2

7—10秒，a=Δv/Δt=12.05-12.35/9.58-7=-0.08m/s2

第三段的加速度为负值，说明做减速运动.

通过以上对博尔特百米赛跑的描述，由粗糙到精细，分为三个层次：

（1）把全程看作匀速直线运动，速度为10.44m/s;

（2）前3秒做加速運动，加速度为4m/s2，速度达到12m/s后做匀速运动;

（3）前3秒做加速运动，加速度为3.33m/s2，速度达到10m/s;之后的4秒内依然加速运动，但是提速变慢，加速度为0.59m/s2，速度达到12.35m/s;最后的大约3秒内，运动缓慢减速，加速度为 -0.08m/s2.

在对百米跑的描述中，通过研究分段平均速度，绘制图象观察速度的变化，自然引出描述提速能力的物理量—加速度，这不仅能让学生体会到建立加速度概念的必要性，也能更容易理解加速度的内涵.这种方法改变了先建立瞬时速度的概念再引入加速度的思路，更符合学生的认知规律.随着分段的增加，对运动的描述就愈加精细，这正是运动学的研究思路，也是极限概念的由来.

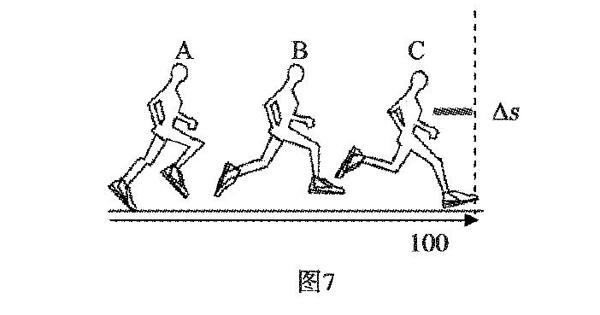
同时，分段速度的研究，为瞬时速度的引入做好了充分铺垫.顺着分段的思路继续向学生发问：怎样把运动的描述再精细化呢？回答是划分更多的段，测量更多的时间和位移.比如，把运动位移等分成20段、30段… 随着段数的增加，速度就趋近于某一时刻或者某一位置的速度.例如，运动员冲刺撞线时的速度，如图7.

根据规定，运动员颈部以下腰部以上的躯干部位撞线，才算到达终点.可以取运动员撞线前的微小位移△s，测量对应的时间△t，然后根据平均速度的定义，当△t趋近0时，v=△s/△t 就是运动员在x=100米处撞线时的瞬时速度.可见，测量瞬时速度，要取很小的位移和对应的时间，而位移及时间段越短，测量就越困难，秒表就不能用了.这为后面的打点计时器、光电门计时器、频闪照相等研究运动的方法埋下伏笔.

通过以上分析，可以对博尔特百米赛跑进行三个层次的描述，从全程平均速度过渡到分段平均速度，从平均速度图象引导出加速度概念，再从分段平均速度抽象出瞬时速度概念.

参考文献：

[1]中华人民共和国教育部.普通高中物理课程标准（2017年版）[M].北京：人民教育出版社，2018.

[2]廖伯琴.普通高中物理课程标准解读[M].北京：高等教育出版社，2018.

[3]阎金铎，郭玉英.中学物理新课程教学概论[M].北京：北京师范大学出版社，2018.

（收稿日期：2019-08-20）