轮腿式爬楼轮椅后腿机构模糊PID控制系统*

2019-11-18狄伟翔曹东兴甘晓萌

传感器与微系统 2019年11期

狄伟翔, 曹东兴, 张琦, 甘晓萌

(河北工业大学机械工程学院,天津 300130)

0 引言

智能爬楼轮椅的出现为老年人及残疾人士的出行提供了一定的方便,但其作为一种复杂的机电产品,要想实现整体的功能,需要各部分的协调配合,为此就必须对每一部分设计一套精准的控制系统。就爬楼轮椅的后腿机构而言,其在运动过程具有高度的非线性,无法对其建立明确的控制模型,且执行构件在运动过程中具有一定延后性。本文控制任务是将后腿机构两滑块的距离调整到上位机下发的目标值,以便准确调整后腿位姿。目前常采用比例—积分—微分(proportion-integration-differentiation,PID)控制或者模糊控制,若采用常规PID控制,控制参数整定较难,且动态特性较差,但其控制精度较高[1];若采用简单模糊控制,由于其只能按档位处理,一般在“区域零”存在着静态误差,但其抗干扰性和动态性能较好[2]。为此,本文将两者结合起来对后腿位姿调节机构进行分段控制,当误差大于某个阈值时,切换到模糊控制,以便提高系统的响应速度;而当误差小于某个阈值时,切换到PID控制,以便消除静态误差,提高控制精度[1～3]。

1 后腿机构的构型与动作要求

1.1 后腿机构运动特性分析

爬楼轮椅的后腿机构主要在轮椅上下楼梯和越障时启动,可以增大攀爬力,辅助轮椅完成上下楼和跨越障碍,同时还能够在一定程度上调整整个轮椅车的重心[4]。整个后腿机构安装于底盘上并通过后腿电机提供动力调节位姿,其传动示意图如图1所示。当后腿电机转动时,如果离合器吸合动力便会通过齿轮组传递到丝杠,进而使滑块1和滑块2沿丝杠滑动。其中,滑块1在水平方向运动,滑块2在竖直方向运动。而滑块通过连杆机构与后腿架连接,这样便可以通过滑块1和滑块2的运动来调节整个后腿机构的位姿。同时在后腿架上安装有排轮,其动力源由排轮电机提供,当后腿架位姿调节到位后,排轮便会与台阶接触,对整个轮椅起到助推作用。

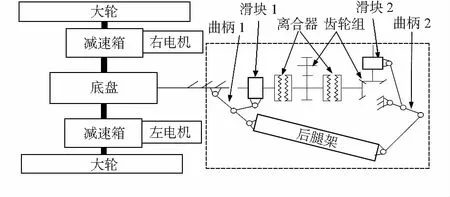
图1 后腿机构传动示意

1.2 传感器安装位置

本项目中爬楼梯轮椅后腿机构属于并联五杆机构,具有两个自由度,分别为两个曲柄的转动,其机构简图如图2所示。杆b1和杆b4称为驱动杆,分别对应于图1中的曲柄1和曲柄2,杆b2代表执行杆(也称作后腿架)。后腿架前后两端为曲柄滑块机构,两滑块运动驱动两曲柄转动,进而带动执行杆运动,最终让后腿架调节到指定的位姿[4]。

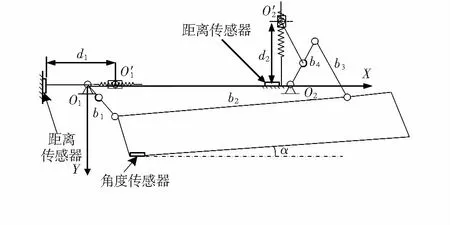
图2 后腿机构简图

为了精确控制执行杆的运动,需要在后腿机构中加入2只距离传感器,以便对后腿运动情况实时监测。传感器安装在机架上,位置如图2所示,分别测量各传感器到滑块O′1的距离d1和到滑块O′2的距离d2。同时,为了监控后腿位姿调整的准确性,还在后腿架上安装了1只角度传感器,测量后腿架与水平面的角度,而在程序处理中还需要结合底盘传感器将其换算为与底盘的角度才有参考价值。

2 后腿控制系统硬件设计[5]

硬件部分主要由控制器、传感器模块、通信模块、步进电机模块、按键及报警模块以及为保证控制器及电机正常工作的辅助模块组成,具体的系统硬件组成框图如图3所示。其中，控制器采用了TMS320F2812,LED和蜂鸣器模块可以实现报警功能;而距离和角度传感器分别选用了夏普红外传感器和MMA8452数字式角度传感器;上位机通信采用RS—232异步串口通信。在对后腿位姿调节过程中加入了离合器,这样电机就可以在离合器断开状态下“空载启动”;而当滑块运动到指定距离后也不需要电机停止,只需让离合器断开,电机维持低速运行即可。这样就方便了下一次位姿调节,同时也避免了电机的“重复启停”问题。

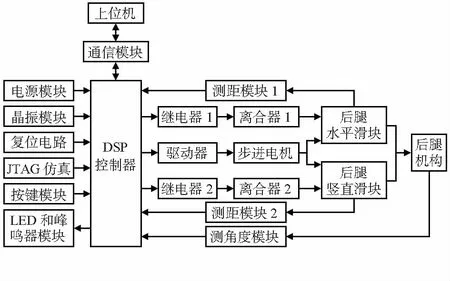
图3 系统硬件框图

3 后腿位姿调节控制器设计

3.1 控制器结构设计

由于后腿是二自由度的五杆机构,其水平方向和竖直方向的运动由离合器分离且完全独立,同时从水平丝杆到竖直丝杠的传动比为1且两丝杆螺距都为5 mm,为此在设计过程中只需要设计一套复合型Fuzzy-PID控制器就可以对后腿的水平运动和竖直运动精确控制,并将其阈值设为5 mm。由于稳态误差主要靠积分环节消除,实际控制过程中只采用了Fuzzy-PI复合控制器,设计得到的控制系统框图如图4所示[6]。

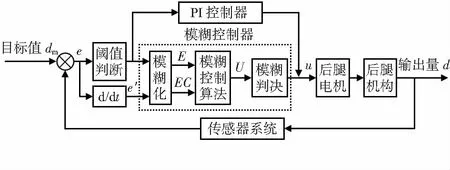
图4 后腿机构复合型Fuzzy-PID系统框图

图4中控制器的输入变量为传感器系统测量的实际距离d与给定目标距离dm之间的偏差e=d-dm及其变化率e′;输出变量为电动机的转速u。常规PID控制算法原理如式(1)

(1)

式中kp为比例系数,Ti为积分时间常数,Td为微分时间常数。该式为连续状态公式,为了便于程序的实现,需要将其离散化,假设采样周期为T,则在KT时刻离散化可得到位置式PID公式(2)

(2)

式中ki=kp·T/Ti为积分系数,kd=kp·Td/T为微分系数,其参数的调节主要根据经验和现场的调试来确定,将微分系数设为0时PID调节便可转换为PI调节。

为了进一步提高积分项的运算精度,从而更好地消除静态误差,可以将式(2)中的矩形积分改为梯形积分,则最终的计算公式为

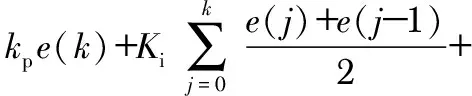
kd[e(k)-e(k-1)]

(3)

比例—积分(proportion-integration,PI)控制器最终采用了式(3)所示的原理,实际控制过程中参数kd为0,并且设置了积分限幅和输出限幅。而模糊控制器选择了一个双输入、单输出结构的二维模糊控制器,这里主要分析模糊控制器的设计过程。

3.2 模糊化方法

3.2.1 偏差E赋值表

后腿机构两滑块的最大运动距离为100 mm,但考虑到后腿位姿在实际调节过程中不可能大幅变化,将其偏差e的基本论域定为[-30,+30]mm便可满足实际需求。如果选定E的论域X={-6,-5,…,-0,+0,…,+5,+6},就可以得到偏差e的量化因子ke=6/30=0.2,其语言变量E选取8个语言值:{PB,PM,PS,PO,NO,NS,NM和NB}来分别表示偏差“正大,正中,正小,正零,负零,负小,负中,负大”。根据实验经验,可以确定出其隶属度函数μ(x)和语言量变量E的赋值表,如表1所示。

表1 E的隶属度函数

3.2.2 偏差变化率EC的赋值表

在实验过程中电机转速较慢,为此滑块运动速度也较慢,通常其偏差变化率维持在6 mm/s内,为此偏差变化率e′的范围为[-6～6]mm/s,并且将该范围每1 mm/s划分一个档位,这样就可以将偏差变化率e′的语言变量EC的论域定为Y={-6,-5,…,0,...,+5,+6},此时偏差变化率的量化因子k′e=6/6=1。EC的语言变量选{PB,PM,PS,O,NS,NM,NB}来分别表示偏差变化率EC“增加很快,增加快,增加慢,不变,减小慢,减小快,减小很快”。根据实验经验,可以确定出模糊子集{PB,…,NB}的隶属度函数μ(x),进而建立语言变量EC的赋值表,如表2所示。

表2 EC的隶属度函数

3.2.3 输出语言变量U的赋值表

模糊控制器的输出量为电机转速,将其分为6个档位(分别为-600,-500,...,500,600 r/min)数值越大电机转速越快,数值前面的正负号代表电机转动的方向,这样便可以将其论域定为[-6,+6],输出量的比例因ku=600/6=100.选取其语言变量值为{PB,PM,PS,O,NS,NM,NB}来分别表示输出变量U“正转快,正转较快,正转慢,停止,反转慢,反转较快,反转快”。通过经验可以确定其模糊子集{PB,...,NB}的隶属度函数μ(x)和其语言变量U的赋值表,如表3所示。

表3 U的隶属度函数

3.3 模糊控制规则的制定

根据实际操作经验,如果实际距离小于目标距离且相差很大,并且具有很大的减小趋势,则此时电机应该快速正转,则此模糊规则表述为

ifE=NB andEC=NB thenU=PB

这样一共可以形成56条控制语句,将这56条语句制成一个表格[6],并称其为后腿位姿调节控制系统的模糊状态表,如表4所示。

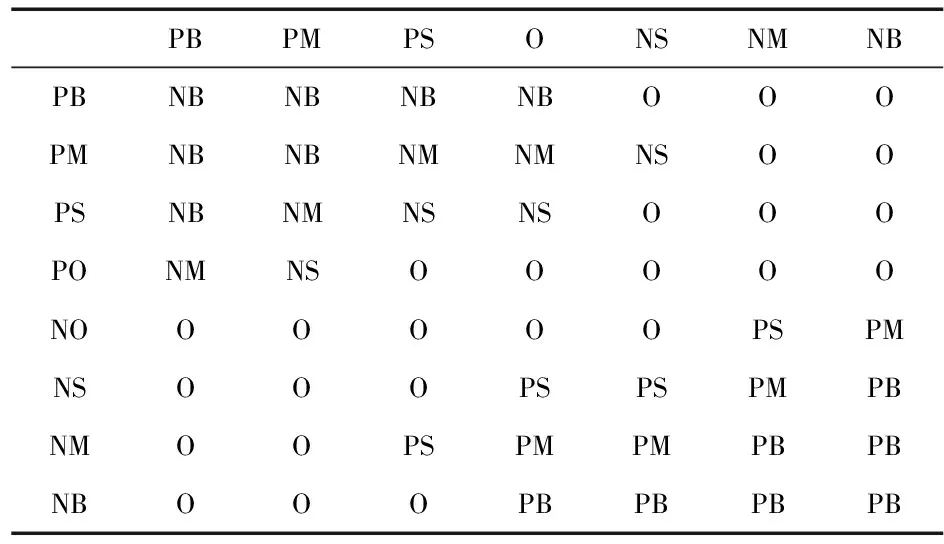
表4 模糊控制规则表

上述表中规则R1按照模糊理论中的关系式可表示为

R1=[(PB)E×(PB)EC]T×(NB)U

(4)

该表格中每条控制规则之间通过“或”关系连接,这样便可得到整个控制系统模糊控制规则的总模糊关系,即

(5)

3.4 模糊决策与模糊控制表的制定

通过模糊规则输出的是一个模糊量,该量并不能直接控制步进电机,为此就需要通过模糊判决将其转换为一个精确量。常用的清晰化算法有最大隶属度法、重心法和加权平均法[6],本文应用重心法对模糊控制器输出解模糊,其是将隶属度函数与横坐标所围面积的重心作为输出量,离散化后的公式如式(6)所示

(6)

式中μN(xi)为其隶属度

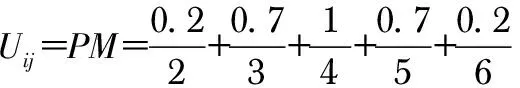
此时得到的“4”便为输出量U的精确量。如果所得结果为小数,程序还需要对其进行“取整”,通过这种方法便可以得到总的模糊控制查询表。将其存于DSP的存储空间中,通过查表子程序实时调用,这样既简化了控制程序的复杂性同时又提高了控制的实时性[7]。

在实际控制过程中,只需要将每一个控制周期内采集得到的实测偏差e(k)和计算得到的偏差变化e(k′)分别乘以量化因子ke和k′e取得对应论域元素表中的元素,然后就可以根据坐标找到对应的控制量,再将其乘以比例因子ku便可以得到最终的电机转速[6]。

4 控制系统测试与实验结果

4.1 系统测试流程

系统测试分为手动测试和自动测试,其中，手动测试是利用按键来完成相应动作,目的是测试后腿机构动作是否流畅;而自动测试是在手动测试完成后,通过上位机向下位机发送数据来自动控制后腿动作。整个测试程序的流程图如图5所示。当上位机根据后腿运动模型下发两滑块运动距离后,下位机会将接收到的数据与传感器采集得到的实际距离对比,进而算出偏差及其变化率,然后通过模糊推理或者PI调节输出电机应该转动的速度,最终控制两滑块运动到目标距离。

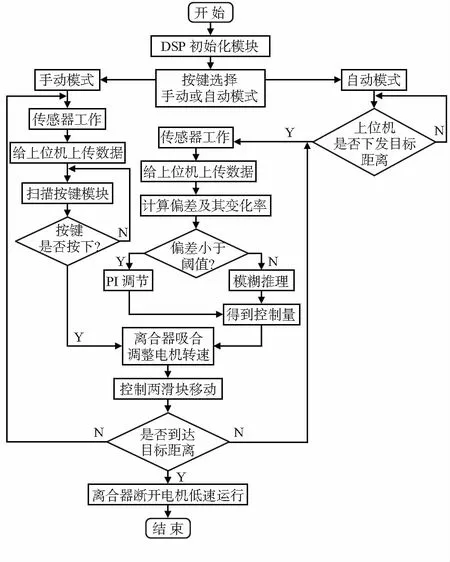
图5 测试程序流程

4.2 实验结果与分析

如图6为爬楼轮椅测试后腿机构越过某障碍时的一组数据,上位机根据行为图模型下发滑块一和滑块二的目标距离为分别为80,50 mm,通过传感器测得滑块一当前距离为62.18 mm,滑块二当前距离为33.21 mm。经过程序的自动调控,最终滑块停留在了目标距离±1 mm的范围内,将后腿机构的位姿调整到了预定角度。然后通过安装于后腿架上排轮的助推作用,成功越过了障碍。通过传感器监测到的实时数据,分别绘制了不同控制策略下d1,d2随时间变化的曲线。

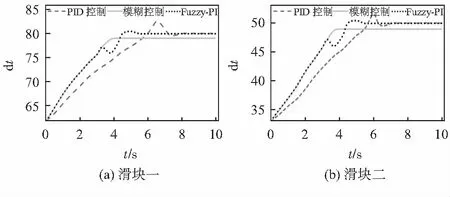
图6 实验测试结果

通过分析滑块一的运动曲线可知,通过常规PID调节大概需要8 s到达目标值,且在调节过程中超调量较大,动态性能较差,但其稳态误差较小。而使用简单模糊控制器系统响应较快,大概需要4 s,但最终存着1～2 mm的静态误差,这是因为模糊控制器按档位处理,而档位零对应一个区间,当偏差处于档位零时系统便认为已经调节到目标距离。而使用复合式Fuzzy-PID调节后,系统响应速度介于二者之间,大概需要5.5 s,具有较好的动态和静态性能,虽然在阈值处会有较小的振荡,但整体控制效果较好,可以达到控制需求。分析滑块二也可以得到同样的结论。但为了让系统的控制效果更加精确,需要对影响因素进行分析,大致有传感器的测量误差和安装误差,电机运行及工作环境对控制硬件的干扰以及控制方法的不完善等[7]。为此今后可以在这几个方面对该控制系统作进一步的优化。