底水油藏特高含水期相渗曲线重构方法及应用

2019-11-18侯亚伟杨东东孙恩慧

石油化工高等学校学报 2019年5期

张东，侯亚伟，杨东东，彭琴，孙恩慧

（中海石油（中国）有限公司曹妃甸作业公司/渤海石油研究院，天津300459）

油水相对渗透率曲线表征油水两相在多孔介质中的渗流规律，是油田开发过程中不可或缺的重要资料。底水稠油油藏处于特高含水期时，水平井波及体积难扩大，但是大量资料表明[1-2]，随着孔隙体积注入倍数的增加，波及区域内驱油效率可再提高。目前行业标准中规定，常规相渗曲线在注水30倍孔隙体积后测取残余油饱和度端点值，而底水油藏理论模型研究表明，特高含水期时主流线区域内孔隙体积冲刷倍数高达上千乃至上万倍，因此常规相渗曲线端点值已经无法准确反映底水油藏特高含水期的生产实际。常规相渗曲线反演方法是基于相渗曲线的一维水驱油理论或者常用的水驱理论曲线计算得到，该过程没有考虑油藏类型、开发方式、井型等因素[3-5]，且计算过程中需要实验条件下测得的端点值数据作为已知参数，导致反演的相渗曲线向矿场推广应用时存在一定偏差[6]。

渤海X油田构造幅度较低，最大圈闭幅度35 m，地层原油黏度分布为 30～425 mPa·s，主要发育为高孔高渗储层，稠油底水油藏储量占比78%。该油田目前已经处于特高含水期，68%的生产井含水大于90%。生产井动态特征表明，底水油藏水平井含水上升快，可采储量主要在高含水以后产出，其中特高含水阶段累产油占可采储量比例达到60%～70%。大量的底水油藏数值模拟研究表明，目前相渗曲线难以精确表征特高含水阶段的水驱油规律，数模预测结果准确性较差。室内实验表明，底水油藏高采液速度下，随着驱替倍数的增加，残余油饱和度可进一步降低，导致常规相渗实验数据难以描述特高含水阶段水驱油规律。

因此，对于水平井开发的底水油藏，常规方法已无法准确反演相渗曲线的形态参数和端点值。针对以上问题，提出了基于遗传算法的底水油藏相渗曲线数值反演方法。

1 底水驱理论模型的建立

该油田油藏类型主要为强底水稠油油藏，相比于常规注水开发油田，底水油藏采用水平井开发，纵向以底水脊进为主，初期含水迅速，递减率大，高含水期维持时间长。通过对实际油藏驱替过程的分析，结合底水油藏水平井油水两相渗流规律，建立了考虑各向异性的油水两相均质底水驱水平井流管模型。模型假设条件为：①地层为均质且各向异性；②忽略毛管力和重力的影响；③底水能量充足，油层底部原始油水界面为恒压边界；④流体和岩石不可压缩；⑤稳定渗流。

如图1所示，底水油藏水平井进入特高含水期后，波及区域趋于稳定，针对水脊剖面，文献中常用数学方法拟合得到水脊半径与水锥高度的关系[7]，如式（1）所示。

式中，r为横向水脊波及半径，m；h为纵向水脊高度，m；a1，a2，a3为常数，与原油黏度、水平与垂向渗透率比值、油层厚度、避水高度、产液水平等因素有关。

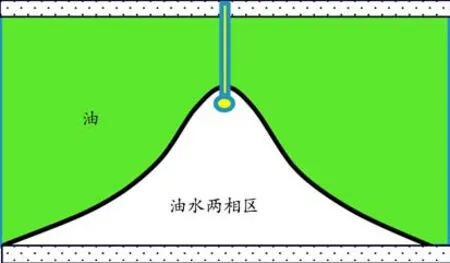
图1 底水油藏水平井波及区域示意Fig.1 Swept volume sketch map of horizontal well in bottom-water reservoir

流管法是研究油藏水驱油机理的一种有效方法之一，可以用来模拟不同注采关系条件下的饱和度分布情况，同时可以计算油田的理论开发指标，流管法贯穿于油田开发的全过程，因此流管法的应用对于指导油田的开发意义深远。假定建立的流管模型驱替过程中多孔介质中流体稳定渗流，流线不变。因此，式（1）可以确定出底水油藏水平井波及区域内不同的流线分布，进而可将模拟区划分为多个流管。为了减小误差，方便模拟计算，每根流管均采用等体积网格剖分方法，剖分结果如图2所示。

图2 底水油藏水脊区域等体积剖分结果Fig.2 Mesh generation of water coning in bottomwater reservoir

流管模型中一维油水两相流动满足Buckley-Leverett方程，在流管坐标系条件下的流动方程为：

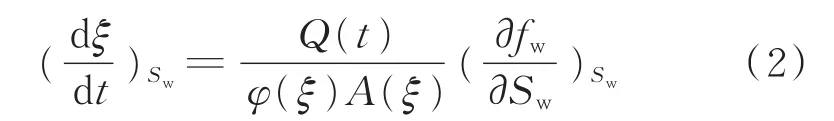
式中，ξ为流管中t时刻某一含水饱和度所对应的位置，m；为Sw处的分流量曲线的导数；φ为孔隙度；A为渗流的横截面积，m2；Q（t）为注入端的累计体积流量，m3。

根据式（2）等饱和度面推进方程的微分形式，计算某时刻各流管的水驱前缘饱和度位置及饱和度变化规律[8]：

引入达西公式，计算各流管中对应的饱和度分布下的相对渗透率值，依据渗流阻力法计算某时刻各流管的流量：

式中，ΔP为流管生产压差，MPa；R为渗流阻力。

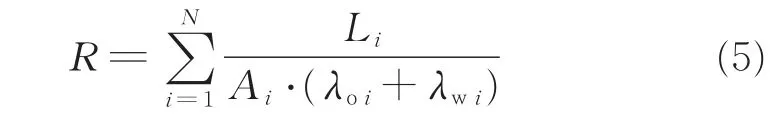
式中，Ai为流管划分某i网格处的渗流面积，m2；Li为某i网格处流管划分的长度，m；λoi、λwi分别为流管划分某i网格处油相和水相的流度；N为流管纵向网格划分个数。

对于每个流管，模拟主要包括底水油藏波及区域的流线分布、前沿推进方程的求解、总流量的求解，以及总流量与时间关系的求解等。因此，通过上述公式，可以建立各流管内流量与时间的关系，将相同时间下的各流管的结果叠加，即可得到波及区域的开发指标情况。

2 遗传算法耦合底水驱理论模型

相渗曲线一般采用指数表达形式进行表述[9]:

式中，krw_Sor为最大水相对渗透率，kro-Swi为初始最大油相相对渗透率，一般归一化后为1；其中Sw为含水饱和度；Swi为束缚水饱和度；Sor为残余油饱和度，Cw、Co分别为水相和油相的相渗形态参数。。

式（6）中，初始含水饱和度可以通过密闭取芯、压汞资料、测井等方法测取[10]，为确定参数；如图3所示，分析相渗曲线表达式的各参数，相渗形态参数Cw、Co以及端点值Sor、krw_Sor，为不确定性参数。目前已知底水油藏大量处于特高含水期的生产井动态资料，通过建立的底水驱理论模型，利用间接的手段可以确定相渗曲线的四个不确定性参数。

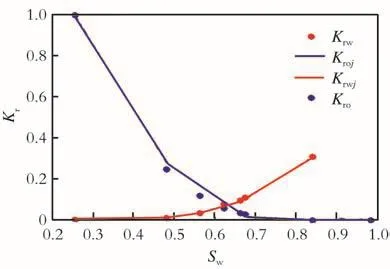
图3 相渗曲线参数分析Fig.3 Parameter analysis of relative permeability curve

遗传算法是模拟达尔文进化论的自然选择和遗传学机理的生物进化过程的计算模型，是一种通过模拟自然进化过程搜索最优解的方法。如图4所示，首先利用已知相渗曲线的特征参数作为初始值，然后产生不同特征参数条件下的相渗曲线作为初始种群，通过底水驱理论模型计算每条相渗曲线对应下的含水率与采出程度理论曲线，将理论曲线与实际曲线作对比，如果不满足终止条件，利用遗传算法将不同特征值相渗曲线进行复制、交叉或变异，产生新的相渗曲线特征参数，循环迭代直至满足终止条件。该过程中利用逐步逼近法不断修正初始值，求得残差最小时对应的相渗曲线特征参数即为最优解，最终重构符合油田实际生产动态的相渗曲线，改善了由于相渗曲线水驱倍数过小（一般30 PV）而导致残余油饱和度偏小的缺陷，丰富了底水油藏特高含水阶段的剩余油认识。

图4 遗传算法耦合底水驱理论模型流程Fig.4 Flow chart of the research coupling genetic algorithm and bottom-water drive model

3 底水油藏相渗曲线反演结果

3.1 底水驱理论模型计算结果

以渤海X油田N1gⅢ砂体的相渗曲线（见图3）及A2H的生产数据为例（见图5），该井2005年投产，3年后进入特高含水期阶段，此后10年含水变化比较平稳，目前累产油32.06×104m3，特高含水阶段累产油占比56%，特高含水期为主要的累产油贡献阶段。目前该井含水率97.0%，日产油37 m3/d。

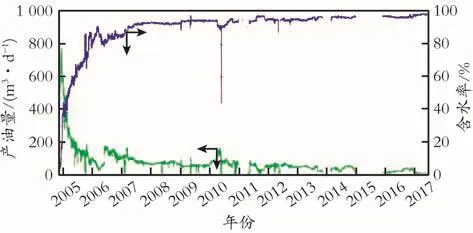
图5 A2H生产井动态曲线Fig.5 The production performance of A2H well

通过两种不同方法计算的含水率与采出程度结果如图6所示。从图6中可以看出，常规相渗曲线结合分流量方程计算结果与实际生产动态数据差异较大，分析原因为，常规方法没有考虑油藏类型、开发方式、井型等因素，无法准确描述该类油藏的水脊规律及生产动态特征；底水驱理论模型计算结果与实际动态数据吻合程度有所改善，但后期含水上升快，拟合效果差，分析原因为，底水油藏特高含水阶段，主要驱替路径冲刷倍数高达1 000倍以上，大量研究表明在此阶段驱油效率仍在增加[11-16]，因此常规相渗曲线测得的残余油饱和度已无法准确描述底水油藏特高含水期的开发规律。

图6 初始相渗曲线计算结果Fig.6 Calculation result of initial relative permeability curve

3.2 遗传算法耦合底水驱理论模型计算结果

通过将遗传算法耦合底水驱理论模型优化计算后，结果如图7所示。从图7中可以看出，该方法优化后的计算结果与实际动态数据吻合程度较好，能够准确描述底水油藏特高含水期时含水率变化趋缓的特征规律。

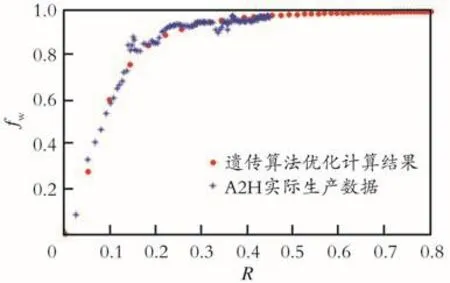
图7 遗传算法优化相渗曲线后计算结果Fig.7 Calculation result of optimized relative permeability curve based on genetic algorithm

3.3 优化后的相渗曲线分析

室内实验测试的相渗曲线，一般反映水平平面流动的储层特点，而底水油藏为由下往上的纵向驱替过程，由于储层岩石的沉积作用，横向水驱和纵向水驱的渗流特征有所差异，因此相应的相渗曲线会出现较大差别。如图8所示，优化后的相渗曲线残余油饱和度0.1，相比原始含油饱和度更低，说明底水油藏特高含水期依靠高PV冲刷倍数可以大幅度提高波及区域内的驱油效率；优化后的相渗曲线反映的是特高含水期底水波及区域内的储层亲水性质，因此等渗点右移，高冲刷倍数后储层亲水性更强。如图9所示，通过对比相渗曲线的含水率与驱油效率关系曲线可以看出，中低含水期时，优化后的相渗曲线与原始相渗曲线含水变化规律基本一致，而特高含水阶段，优化后的相渗曲线含水变化相对缓慢，这种趋势和规律更加符合油田实际生产动态。

图8 遗传算法优化相渗曲线Fig.8 Optimized relative permeability curve based on genetic algorithm

图9 相渗曲线计算结果对比分析Fig.9 Analysis of optimized relative permeability curve

3.4 数模验证及方法应用

将优化后的相渗曲线带入数模计算，N1gⅢ砂体的A2H井的拟合情况如图10所示。

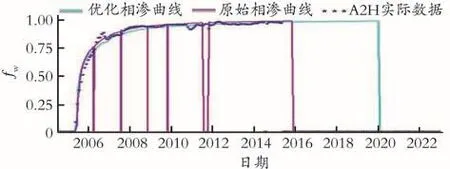
图10 优化后相渗代入后数模预测曲线Fig.10 The curves of numerical calculation based on optimized relative permeability curve

由图10可以看出，相比A2H井的实际数据，原始相渗曲线拟合含水率曲线偏高，优化后的相渗曲线拟合结果更加符合该井实际的含水变化规律。

技术可采储量对比情况如图11所示。

图11 技术可采储量对比柱状图Fig.11 The histogram of technical reserves compared with practical production

从图10、11中可以看出，原始相渗曲线预测该井至2015年底含水率达98%，由于含水率计算偏高，技术可采储量预测仅28.18万m3，该结果小于目前实际累产油量31.68万m3，与实际生产数据相矛盾；优化后的相渗曲线预测含水率达98%时生产时间到2020年，技术可采储量为38.14万m3，且与原始相渗曲线数模结果相比，技术可采储量预测增加10万m3。因此，通过该方法实现了底水油藏特高含水期的动态数据精细拟合，加深了特高含水期的老井剩余潜力认识，该研究可为底水油藏特高含水期老井井网的动态预测和精细挖潜提供一定的理论依据。