基于二维双向PCA的手写数字识别算法研究
2019-11-18郭春妮高瑜翔黄坤超
郭春妮,高瑜翔,黄坤超
(1.成都信息工程大学 通信工程学院,四川 成都 610225;2.中国西南电子技术研究所,四川 成都 610036)
0 引言
离线手写数字识别是模式识别应用中的重要问题之一[1],它是在没有人工交互的情况下从0~9识别和分类手写数字的方法。近年来,已经有很多学者提出了不同的识别方法来解决识别率和识别速度的问题。数字识别主要分为2步:① 特征提取[2];② 分类识别。其中,特征提取在数字识别系统中有着举足轻重的地位。主分量分析(PCA)作为一种十分有效的方法,在特征提取中发挥着重大的作用。
传统的KNN算法识别率和识别速度均不高;学者胡君萍提出的PCA结合KNN的识别算法[3],其识别率和识别速度均有提高,但二者相互矛盾,且需要将二维矩阵转换为一维向量,不能精确计算协方差[4];针对一维上PCA算法的不足,学者王军平提出了2DPCA[5]的特征提取,该方法不需要进行二维到一维的转换,而是直接计算图像样本矩阵的协方差,有效地解决了PCA算法带来的问题,其识别速度确有改善,但识别率仍有待提高。
2DPCA的特征提取中,仅对样本的行进行了降维,也就是提取的特征矩阵(p×n)行的维度p要小于原矩阵(m×n)行的维度m[6],但是该特征矩阵还是较大,使得KNN算法中欧式距离的计算量也较大,为了减少欧式距离的计算量[7],提出用更小的矩阵来代替样本的特征,因此,本文对2DPCA算法进行了改进,提出了二维双向主分量分析(2DDPCA)算法,并采用MINIST手写数据集[8],选取了0~9各100张图像作为训练样本,各50张作为测试样本,训练样本和测试样本彼此独立,没有交集,对所提出的算法进行了测试仿真。
1 2DDPCA理论
1.1 算法原理
假设X是一个n维的单位列向量,A表示要处理的m×n的样本矩阵,通过Y1=AX的线性变换[9]将A投影到X上,得到Y1,再将Y1通过Y=Y1Z的线性变换投影到Z上,得到的Y称为图像A的特征图像[10]。
下面以如何确定最佳的投影向量X为例,阐述寻找最佳投影向量[11]的原理:
通过投影到X上的样本的整体散度,来确定最佳的投影向量X,样本的总体散度[12]为:
J(X)=tr(SX),
(1)
式中,SX表示样本的投影特征向量构成的协方差矩阵[13],表示为:
SX=E(Y1-EY1)(Y1-EY1)T=E[AX-E(AX)][AX-E(AX)]T=E[(A-EA)X][(A-EA)X]T=XT[E(A-EA)T(A-EA)]X。
(2)
因此,
J(X)=XT[E(A-EA)T(A-EA)]X。
(3)
定义矩阵GT为图像的散度矩阵:
GT=E(A-EA)T(A-EA)。
(4)
可以得到:
J(X)=XTGTX。
(5)
寻找一组最优的正交投影向量:X1,X2,…,Xd,使得J(X)最大化。经验证,这组最优的投影向量,即是由GT的前d个最大的特征值对应的特征向量组成的。
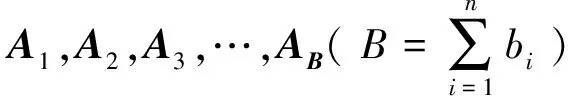
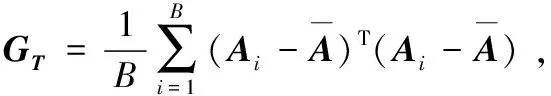
(6)
(7)
1.2 算法流程
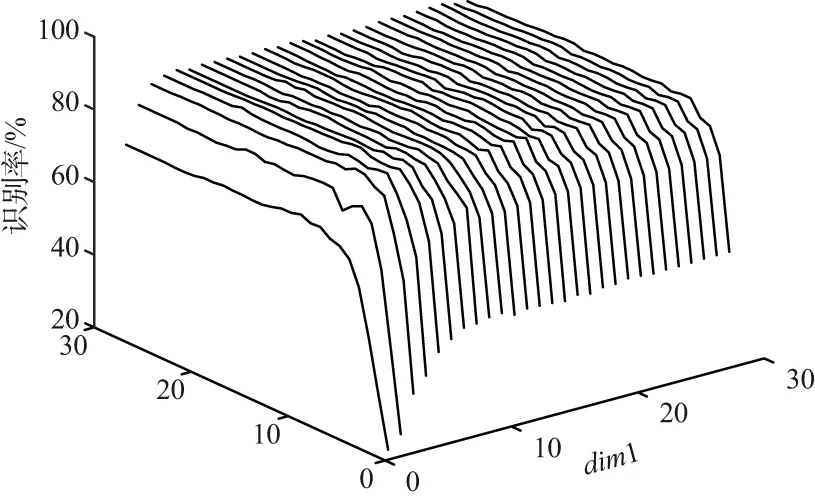
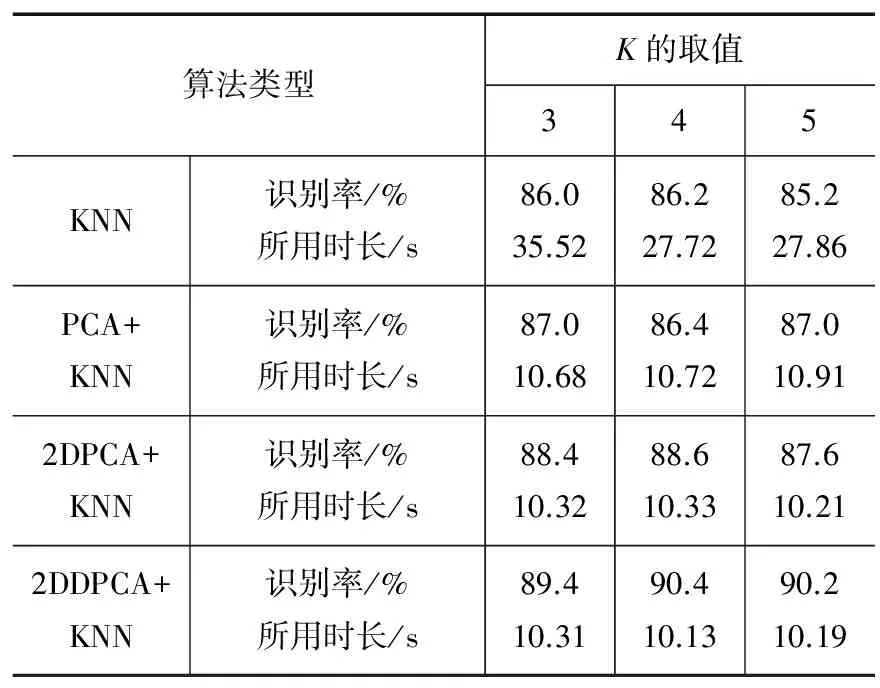
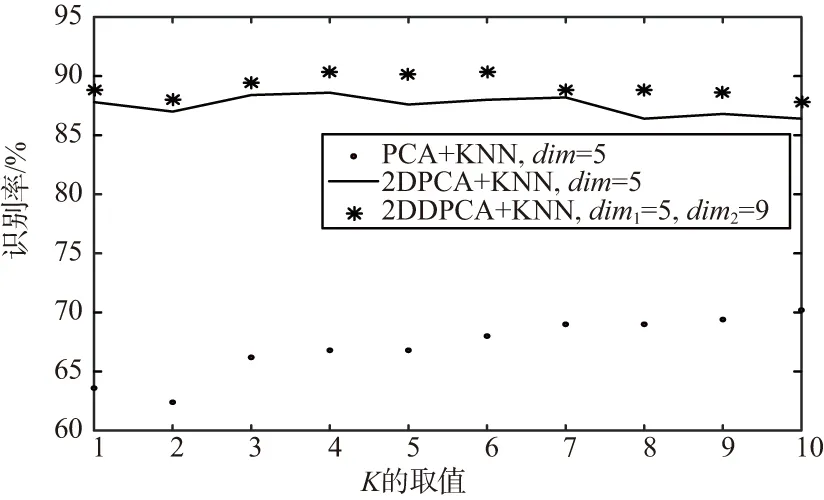
① 通过式(6)列出样本A的散度矩阵GT,计算其特征值及特征向量,选出前p(p ② 将Y1作为第二次特征提取的样本,令Y1=Ok∈Rm×p,计算Y1也就是Ok的散度矩阵G: (8) (9) 通过散度矩阵计算其特征值及特征向量,选出其q(q 本实验主要对手写数字识别系统进行了设计分析,采用2DDPCA特征提取和KNN分类算法相结合的方法进行识别,同时对比了3种特征提取方法(PCA,2DPCA,2DDPCA)在识别中的效果。本实验在MATLAB平台下进行,具体实现流程如下: (1)实验准备:选取MINIST数据库中的1 500张图像进行编号和分类,新建2个文件夹,分别为训练集和测试集。其中,训练集包含0~9共十类样本,每一类样本组成一个文件夹单独存放,且每类中包含100张样本图像;测试集也同样操作,每类中包含50张样本图像。 (2)样本预处理:由于MINIST数据库的图像是统一大小的,因此不需要对样本图像的大小进行处理。只需要将样本图像转化二值图像[14],即针对每一个像素点,将图像处理成只用0和1表示的矩阵[15]。 (3)特征提取:分别使用PCA,2DPCA,2DDPCA三种算法,通过训练样本[16],求取特征矩阵X。 将训练样本组成的矩阵train转化为一维向量train_data,求train_data协方差的特征值及对应的特征向量,取前dim个最大的特征值对应的特征向量组成特征矩阵X。将训练样本train_data投影到X上,得到训练的特征图像train_Y,再将某一张测试样本图像转换为一维向量test_data,以同样的方式将test_data投影到X上,得到测试的特征图像test_Y。 按照2.2小节所述的算法流程进行两次特征提取,得到行和列都进行降维的特征图像。 (4)分类识别:运用KNN算法[17],计算train_Y和test_Y之间的欧式距离[18],将距离从小到大排序,并保存对应的编号,选取其中K个最小的距离,即测试对象的近邻,寻找每个距离对应的训练样本图像,记录每个图像对应的编号,根据这K个编号所属的类别,取其中占数最多的类别作为识别结果。 本实验采用了MINIST数据库中的1 500个样本,其中训练样本1 000个,测试样本500个。训练样本和测试样本各10类,分别是0~9的样本,样本为28×28像素大小的图像。通过特征提取和KNN算法分类识别,在MATLAB平台上实现仿真,对仿真结果进行如下分析: 使用2DDPCA进行特征提取,然后使用KNN算法进行数字分类识别。按照需求从命令行窗口输入KNN算法中的参数K,以及2DDPCA算法中矩阵行和列分别需要降低的维度dim1,dim2。遍历所有的测试样本,每一次循环都会显示识别结果,待所有样本都被识别完后,还会显示识别成功和失败的样本个数,同时显示识别率。 由于在选定K值时,该算法的识别率随dim1,dim2变化的数据量太大,这里将其绘制成如图1所示的曲线图,可以看出该算法的识别率和dim1,dim2的选取息息相关,dim1达到7时,识别率随dim2的波动趋于平稳,当dim2达到4时,识别率随dim1的波动也趋于平稳,因此选取适当的dim1和dim2的值即可,其对应的主分量矩阵几乎已经能够代替整个图像的特征,因此不论dim1,dim2如何变化,其识别率不会有很大的波动。 图1 2DDPCA算法识别率随2个维度的变化曲线 将该算法和其他算法进行对比,通过大量的仿真,得到相同条件下几种不同算法的识别率以及所用时长,具体数据如表1所示。 表1 4种算法的识别效果对比 算法类型K的取值345KNN识别率/%所用时长/s86.035.5286.227.7285.227.86PCA+KNN识别率/%所用时长/s87.010.6886.410.7287.010.912DPCA+KNN识别率/%所用时长/s88.410.3288.610.3387.610.212DDPCA+KNN识别率/%所用时长/s89.410.3190.410.1390.210.19 根据上表,可以得出结论:使用PCA及KNN的联合识别算法时,选取一定的dim值,其识别率比单独使用KNN算法的识别率要高,且识别速度更快;当使用2DPCA及KNN的联合算法,其识别率比使用PCA算法和单独使用KNN算法都要高,而其识别速度与使用PCA算法相差不大;当使用2DDPCA及KNN的联合算法,选取合适的dim1和dim2,其识别率比前3种算法都高,而识别速度和2DPCA几乎没有差别。在PCA算法中,需要将二维矩阵变换成一维向量,如果要达到更高的识别率,则主分量的维度会相应增大,此时的识别速度会减慢,因此,对于PCA算法来说,要想得到较高的识别率,需要牺牲识别速度。2DDPCA相对于2DPCA算法来说,多一次特征提取的过程,因此在特征提取过程中耗费的时间会相对多一些,但在识别过程中,由于2DDPCA的特征矩阵比2DPCA的特征矩阵小,在识别过程中,欧式距离的计算量也就相对较小,所以这2种算法的识别速度几乎没有差别。 在相同的维度下,分别对3种算法进行仿真,多次仿真后得到的识别率变化曲线如图2所示。 图2 3种不同PCA算法在相同dim下的识别率 从实验数据分析折线图可以看出,在相同的维度下,2DDPCA及KNN联合的识别算法在不同K值下识别的效果最好。2DDPCA相比于2DPCA,多进行了一次特征提取,因此其提取的特征更能准确表征原图像,从而使得识别效果更佳。 本文提出了基于2DDPCA结合KNN的手写数字识别算法,并分析仿真比较了与其他3种算法在识别速率与识别率方面的优劣性。从理论上来说,2DDPCA算法不仅是直接对矩阵进行处理,还对行和列都进行了降维,实现了2次特征提取的同时,更进一步降低了特征矩阵的大小。因此,图像的特征信息更加准确,从而能够在不牺牲识别速度的同时,识别率得到一定提高。
2 识别过程
3 实验仿真与分析
4 结束语
