预期对路径整合的影响*
2019-11-18张为威黄建平宛小昂
张为威 黄建平 宛小昂
预期对路径整合的影响
张为威 黄建平 宛小昂
(清华大学心理学系, 北京 100084)
人们通过整合自身运动信息进行的空间巡航称为路径整合。本研究采用头盔式虚拟现实和分段式虚拟迷宫, 探究个体的预期如何影响其路径整合的准确性。任务要求被试从包含4个或8个路段的外出路径的起点出发, 行经所有路段后到达外出路径的终点, 再从终点直接返回起点。三组被试在实验前接受不同的指导语, 并因此对正确返航距离产生不同的预期。实验结果表明, 个体返回起点的行为反应受到外出路径特点的影响, 而且反应的准确性在实际情形违背预期时比符合预期时更低。这样的研究结果表明, 预期作为一种非感知觉因素而影响人们进行路径整合, 体现了人类路径整合的高度适应性和策略性。
预期; 路径整合; 空间巡航; 虚拟现实
1 引言
寻路是人类生存的重要技能。当环境中饱含丰富的路标及其他视觉线索时, 人们可以依赖这些环境线索完成空间巡航(navigation)。如果环境中缺少路标线索, 人们也可以通过整合自身运动信息来更新自身与行程起点之间的空间关系, 即进行路径整合(李丹, 杨昭宁, 2015; 过继成思, 宛小昂, 2014; 周佳树, 张侃, 2005), 并通过多个相互独立的路径整合进行空间更新并获得动态的认知地图(Wang, 2016)。路径整合所依赖的自身运动信息可以是来自于身体内部的前庭觉和本体觉(Loomis et al., 1993; Sholl, 1989), 即非视觉路径整合; 路径整合也可以依赖于来自外部环境的光流(Riecke, van Veen, & Bülthoff, 2002), 即视觉路径整合。当光流和体感信息同时存在时, 人们也可以将这两类自身运动信息进行整合(Ellmore & Mcnaughton, 2004; Kearns, Warren, Duchon, & Tarr, 2002; Wan, Wang, & Crowell, 2010)。个体对自身运动信息进行认知加工, 主要依赖的脑区是位于顶叶的内上颞区和顶内沟腹侧区(张弢, 李胜光, 2011)。具体到路径整合, 右侧颞叶对非视觉路径整合非常重要(Worsley et al., 2001), 海马和颞中回在视觉路径整合中发挥重要作用(Wolbers, Wiener, Mallot, & Büchel, 2007), 压部后皮层和海马旁回在路径整合的信息加工阶段也很关键(Chrastil, Sherrill, Hasselmo, & Stern, 2016)。
人类路径整合研究常常采用路径完成(path completion)的范式, 也称为返回起点任务(Klatzky et al., 1990; Loomis et al., 1993)。该任务采用多个路段组成的外出路径, 要求被试从起点出发并行经所有路段, 再从外出路径的终点直线返回起点。也就是说, 该任务要求被试通过路径整合来估计外出路径终点与起点之间的相对距离与方向。但是, 被试返回起点的行为表现往往并不完美, 对距离和方向的估计都可能出现误差, 而实际返回的地点往往并不是外出路径真正的起点。因此, 路径整合的准确性, 经常通过被试进行路径完成任务时的位置误差(即外出路径的真正起点到被试实际返回的地点之间的直线距离)来进行衡量。而被试在对距离和方向进行估计时也可能存在系统误差, 即因为一种有偏差的倾向性而导致反应的误差总是沿着一个方向的, 例如总是高估或总是低估(宛小昂, 2016)。这些系统误差可以采用符号距离误差(signed distance error)和符号角度误差(signed angular error)来进行衡量。符号误差是被试的实际反应与正确的反应之间的差值, 正值表示高估, 而负值表示低估。
早期的人类路径整合研究更多感觉因素对路径整合的影响, 而近期研究则揭示了人类路径整合也受到非感觉因素的影响。首先, Philbeck和O’Leary (2005)发现如果让被试在进行非视觉路径整合前预览并记忆路标的位置, 被试在其后进行路径整合时的反应一致性会显著提高。Zhao和Warren (2015)的研究也表明, 被试可以通过整合路标和路径整合提供的信息提高自己行为反应中的一致性。因此, 预览路标帮助被试更加准确地估计距离, 而对路标的记忆影响了被试其后进行的非视觉路径整合。第二, 过继成思和宛小昂(2015)让被试在具有同样空间结构的外出路径上反复地进行路径完成任务, 结果发现被试的路径整合随着重复的次数增加而变得更快、更准确, 表明了经验对路径整合的影响。第三, 过继成思等人(2019)通过指导语操纵了被试对于返回地点的预知, 结果表明预先知道返回地点使被试能够采取更具有适应性的策略, 忽略路标出现或数量增加导致的干扰, 有效地减少工作记忆负荷, 改善路径整合的表现。Guo, Huang和Wan (2019)探讨了对外出路径的选择权如何影响路径整合, 结果表明能够自己选择外出路径会改善被试的路径整合表现, 而先前的路径整合经验也会影响他们在选择外出路径时采用的策略。
这些研究均体现了非感觉因素对人类路径整合的促进。路径整合也可能受到了预期的影响。被试可能存在一种直觉的判断, 认为如果外出路径中包含路段个数越多, 则终点和起点之间的距离也就有可能更远(Wan, Wang, & Crowell, 2012)。但是, 一些研究先后检验了外出路径中的路段个数对路径完成任务成绩的影响, 却获得了不尽一致的结果。Klatzky等人(1990)请被试进行非视觉路径完成任务, 结果表明被试在外出路径的路段个数从一个上升到三个时对起点方向估计变得更不准确, 反应时也随之增加。但是, Wiener和Mallot (2006)采用虚拟现实工具请被试进行基于光流的视觉路径完成任务, 发现被试在外出路径包含4或5个路段时的指出起点方向比外出路径包含2或3个路段时更快、更准确。Wan等人(2013)采用虚拟现实工具让被试完成基于混合的光流信息和身体感觉信息的路径完成任务, 结果发现当外出路径包含的路段从少变多时, 被试返回起点的误差增加了, 而反应时没有发生相应的变化。一种可能性是, 研究者为了获得严格的实验控制而对外出路径进行的设置影响了实验结果。Wiener和Mallot (2006)在控制外出路径的总长度和旋转的总角度的条件下将路段的个数从2个逐渐增加至5个。而Wan等(2013)在他们的实验二中通过正交的实验设计使包含4个或8个路段的外出路径的终点和起点之间的直线距离(即正确返航距离)为3、6或9米, 使正确返航距离与路段的个数无关。这些设置与人们的日常生活经验不符。如果被试根据日常生活经验而产生“经过的路段越多则距离起点也越远”的预期(expectation), 而实验的情形又反复违背这种预期(violation of expectation), 就有可能对被试返回起点的行为产生影响。
预期指人们对未来的事件、情感或结果的信念与预测。对预期违背事件的认知加工与纹状体结构有关(D’Astolfo & Rief, 2017; Garrison,Erdeniz, & Done, 2013), 尤其是右侧壳核(Huang, Wang, Sui, & Wan, 2019)。但是, 目前尚未有实验研究系统探索过预期对人类路径整合的影响, 也没有检验过预期违背对返回起点行为的影响。因此, 本研究以虚拟现实为工具, 操纵被试对正确返航距离的预期, 分别设置符合和违背预期的实验条件, 检验期望如何影响基于混合的光流信息和体感信息的路径整合。在实验开始前, 本研究分别给予三组被试不同的指导语, 即告知他们实验中外出路径包含的路段个数与正确返航距离存在正相关、负相关、或无相关的关系。而实际情况是, 实验采用正交设计, 将包含4个或8个路段的外出路径的正确返航距离设置为不同的水平(5、10、或15米), 即实验中出现的路段个数与正确返航距离之间实际是无相关的。对于正相关信念和负相关信念这两组被试, 实验中会分别出现明显的符合违背与违背预期的情况。具体而言, 对于正相关信念组, 4个路段的外出路径的正确返航距离很短(5米)与8个路段的外出路径的正确返航距离很长(15米)最符合预期; 而4个路段的外出路径的正确返航距离很长(15米)与8个路段的外出路径的正确返航距离很短(5米)是最明显的违背预期。相反, 对于负相关信念组, 4个路段的外出路径的正确返航距离很长(15米)与8个路段的外出路径的正确返航距离很短(5米)最符合预期; 而4个路段的外出路径的正确返航距离很短(5米)与8个路段的外出路径的正确返航距离很长(15米)是最明显的预期违背。
因此, 本研究的实验设计允许我们比较符合预期和违背预期条件下被试的路径整合成绩。本研究的假设主要有4个。首先, 我们假设被试在预期违背条件下的路径整合准确性低于预期符合条件下。第二, 当被试预期经过的路段越多则与距离起点的距离也越远(即持有正相关信念)时, 则他们在外出路径包含8个路段时会比不具有这种预期的被试(即负相关信念组和无相关信念组)更加明显地高估返航距离, 导致路径整合的错误增加。第三, 当被试预期经过的路段越多则与距离起点的距离也越近(即持有负相关信念)时, 则他们在外出路径包含4个路段时会比不具有这种预期的被试(即正相关信念组和无相关信念组)更加明显地高估返航距离, 导致路径整合的错误增加。第四, 当被试预期路段和返航距离之间没有关系(即持有无相关信念)时, 由于实际情况符合他们的预期, 他们的任务成绩会优于两外两组被试(即正相关信念组和负相关信念组)。
2 方法
2.1 被试
48名清华大学的学生参与了本实验, 男女各半。他们的年龄在18至25岁之间, 平均19.8岁, 标准差为1.5岁。每位被试在完成实验后会获得心理学入门课程的实验学分或40元人民币作为实验报酬。我们采用Gpower软件对实验样本量进行估计, 预期效应量为0.25, 而统计效力1−β为0.95, 则预计总样本为45人。实际样本量与计划样本量基本一致。
2.2 仪器和材料
实验在清华大学心理学系的虚拟现实实验室进行, 实验采用的设备是nVisor SX60头盔式虚拟现实。头盔内的显示器的刷新频率为60 Hz, 分辨率为1280×1024像素, 视野为44°(水平) × 34°(竖直)。被试在实验中手持罗技F710无线游戏手柄, 与虚拟场景进行交互。本实验采用的外出路径参数通过Matlab进行计算, 实验进程通过Vizard软件来控制并记录数据, 而虚拟场景则通过3D Studio Max软件创建并渲染。
本研究参考了Wan等(2013)和过继成思等(2015, 2019)对于虚拟场景的设置, 采用分段式迷宫作为路径完成任务中的外出路径。每个外出路径包括4或8个路段, 每个路段长3或5米, 宽1米, 高2.2米, 两端为半圆形。前后两个路段的夹角在30到150度之间, 而外出路径的起点和终点之间的直线距离(正确返航距离)为5、10或15米。如图1所示, 被试从外出路径的起点(H)出发, 经过包含4个或8个路段分别到达终点E4或E8, 而不同外出路径的正确返航距离C4和C8是相同的。

图1 外出路径的平面俯瞰图示例。H代表外出路径的起点, E4和E8分别代表包含4个和8个路段的外出路径的终点, 而这两个外出路径的正确返航距离是相同的, 即C4 = C8。
计算机按照实验设置为每个试次随机生成符合上述条件的外出路径, 包括路段个数(4或8个)、正确返航距离(5、10或15米)、路段长度(3或5米), 以及两个路段的夹角(30到150度之间, 顺时针或逆时针均可)。实验进行过程中, 每次只向被试呈现一个路段。每个试次中呈现的外出路径均不相同, 且被试在前一个试次实际返回的地点则为下一个试次的起点。当被试到达外出路径的终点之后, 在被试选择的方向会出现100米长的走廊, 供被试返回起点。外出路径和返航路径分别通过灰色和土黄色的墙纸进行区别。
与过继成思等(2015)和(2019)的研究类似, 本实验由于头盔式虚拟现实设备与空间的限制, 使得被试在本实验中的直线前进是靠按键完成虚拟的运动, 因此对于直线运动的估计主要依赖于光流。但是, 被试身体的旋转则是通过真实地旋转身体而完成的, 使被试能结合光流和身体信息两种信息来估计转向。
2.3 设计和流程
本研究采用相关性信念(正相关、负相关、或无相关) × 2(路段个数:4或8) × 3(正确返航距离:5、10、或15米)的混合设计。相关性信念为组间变量, 路段个数和正确返航距离为组内变量。被试被随机分为三组, 每组男女各半, 在实验前接受不同的指导语。第一组被试接受的指导语中指出, 路段个数与正确返航距离之间存在正相关, 这组被试被称为正相关信念组; 第二组被试接受的指导语中指出, 路段个数与正确返航距离之间存在负相关, 这组被试被称为负相关信念组; 第三组被试接受的指导语中指出, 路段个数与正确返航距离之间无相关, 这组被试被称为无相关信念组。每位被试完成24个试次, 且所有试次以随机顺序呈现。被试在正式实验开始前会进行练习, 但实验的任何阶段不对被试的反应正确与否提供反馈。
如图2所示, 每个试次开始时, 被试位于外出路径第一个路段的起点(见图2A)。被试通过按键在该路段中以每秒1.5米的速度虚拟前进而身体保持不动, 并在到达该路段终点后按照面前出现的红色箭头指向转动身体至面向下一个路段(见图2B)。如此反复进行, 直至被试到达外出路径的终点, 迷宫墙纸的颜色由灰色变为土黄色(见图2C)。接下来, 任务要求被试转动身体面向外出路径的起点并按键确认。一条100米长的返回路径会出现在被试选择的方向(见图2D), 然后被试通过按键在该路径中虚拟地前进, 直至到达他所认为的起点位置并按键确认。因此, 被试通过光流信息感知运动的距离, 而通过光流信息和体感信息感知旋转, 并以这些自身运动信息为基础进行路径整合。
2.4 数据编码
一方面, 本实验主要通过位置误差来衡量路径整合的准确性, 并同时分析反应时以探明准确率——速度权衡的影响。位置误差指被试实际回到的位置和外出路径起点位置之间的直线距离, 这个距离越小则表明被试实际到达的地点越接近起点, 即路径完成的成绩越好。另一方面, 本实验也通过符号距离误差和符号角度误差来衡量路径整合的系统误差。其中, 符号距离误差是被试的反应距离(返航时实际行进的距离)和正确返航距离之间的差值, 正值说明被试高估了距离, 而负值说明低估了距离。而符号角度误差则是被试的实际转向(到达外出路径终点后旋转身体以面向起点的转向角度)与正确转向(要准确返回起点应该转向的角度)之间的差值, 正值说明高估了转向, 而负值说明低估了转向。
3 结果
本实验中所有被试均完成了全部实验, 但有一位被试在某一实验条件下的试次全部无效, 因此其数据没有纳入分析; 其他被试在个别试次中因提前误按反应键(距离或方向反应为0)而导致数据无效, 这些无效试次没有纳入数据分析, 占总数据量的6.3%。

图2 虚拟场景与路径完成任务流程示意图。(A)试次开始时被试面向第一个路段; (B)被试到达第一个路段的末端并按照提示箭头向左旋转; (C)被试行经所有路段后到达外出路径的终点, 此时迷宫墙纸改变颜色; (D)被试做出方向反应后, 一条长走廊出现在其所选方向供被试做出距离反应。
3.1 路径完成准确性的基本结果
各种实验条件下的平均位置误差和反应时如图3所示, 误差线表示标准误。首先, 我们对平均误差数据和反应时数据进行了相关性信念(路段个数与正确返航距离之间正相关、负相关、或无相关) × 2(路段个数:4或8) × 3(正确返航距离:5、10、或15米)的混合方差分析, 其中相关性信念为组间变量, 路段数和正确返航距离为组内变量。路段个数在位置误差上的主效应显著,(1, 44) = 84.96,< 0.001, η= 0.66, 但是路段个数与相关性信念之间的交互作用也在位置误差上显著,(2, 44) = 3.57,= 0.04, η= 0.14。正确返航距离的主效应也在位置误差上显著,(2, 88) = 25.56,< 0.001, η= 0.37。经Bonferroni校正后的成对比较表明, 被试的位置误差在正确距离为5米时最小(12.1 m),s > 6.03,s < 0.001, Cohen’ss > 0.87, 差异的95% CI分别为 [1.3, 3.2]和[1.8, 4.3] ; 而后两种条件下的位置误差(14.4 m和15.2 m)之间没有显著差异,(46) = 1.64,= 0.11。其他主效应或交互作用在位置误差数据上均未达到显著水平,s < 2.69,s > 0.08, 且任何主效应或交互作用在反应时数据上均不显著,s < 2.51,s > 0.08。

图3 不同路段个数和正确返航距离的外出路径的平均位置误差和反应时
为了解释路段个数与相关性信念在位置误差数据上的交互作用, 我们合并了不同正确返航距离条件下的数据, 然后对每种路段个数进行相关性信念的简单效应分析。当外出路径包含4个路段时, 相关性信念的主效应不显著,(2, 44) = 1.32,= 0.28。当外出路径包括8个路段时, 相关性信念的主效应显著,(2, 44) = 3.49,= 0.04, η= 014。经Bonferroni校正后的成对比较表明, 正相关信念组的位置误差(20.7 m)显著大于负相关信念组(14.1 m),(29) = 2.19,= 0.05, Cohen’s= 0.59, 差异的95% CI为 [0.0, 13.3], 而无相关信念组的位置误差(15.4 m)与另外两组之间的差异均不显著,s < 1.12,s > 0.14。
3.2 预期对路径完成准确性的影响
如前文所述, 4个路段的外出路径的正确返航距离很短(5米)与8个路段的外出路径的正确返航距离很长(15米)最符合正相关信念组的预期, 却最为明显地违背负相关信念组的预期; 4个路段的外出路径的正确返航距离很长(15米)与8个路段的外出路径的正确返航距离很短(5米)明显违背预期正相关信念组的预期, 却最符合负相关信念组的预期。因此, 我们对正相关信念组和负相关信念组在正确返航距离为5米和15米时的位置误差和反应时数据进行了重新编码、合并, 结果如图4所示, 误差线表示标准误。我们对这些数据进行2(路段个数:4或8) × 2(预期:符合或违背)的重复测量方差分析。预期的主效应在位置误差上显著,(1, 30) = 5.51,= 0.026, η= 0.16, 表明位置误差在预期违背时(14.9 m)显著大于符合预期时(13.4 m), 差异的95% CI为 [0.2, 2.8] 。路段个数的主效应在位置误差上也显著,(1, 30) = 41.29,< 0.001, η= 0.58, 表明位置误差在经8个路段后(17.2 m)显著大于经4个路段后(11.2 m), 差异的95% CI为 [4.1, 7.9] 。但是, 预期与路段个数的交互作用在位置误差上不显著,(1, 30) = 0.02,= 0.89。任何主效应或交互作用在反应时数据上也均不显著,s < 0.17,s > 0.68。
3.3 路径完成系统误差的基本结果
各种实验条件下的平均符号距离误差和符号角度误差如图5所示, 误差线表示标准误。
我们对符号距离误差和符号角度误差的数据进行了相关性信念 × 路段个数 × 正确返航距离的混合方差分析。对于符号距离误差而言, 路段个数的主效应显著,(1, 44) = 35.84,< 0.001, η= 0.45, 正确返航距离的主效应显著,(2, 88) = 187.79,< 0.001, η= 0.81, 路段个数与正确返航距离之间的交互作用显著,(2, 88) = 9.17,< 0.001, η= 0.17, 而且路段个数与相关性信念之间的交互作用也显著,(2, 44) = 10.67,< 0.001, η= 0.33。对于符号角度误差而言, 路段个数的主效应显著,(1, 44) = 18.04,< 0.001, η= 0.29。被试在外出路径包括4个路段(18 deg)和8个路段(43 deg)时均高估了转向(符号误差显著大于0),s > 4.69,s < 0.001, Cohen’ss > 1.38, 而这种高估倾向在外出路径包含8个路段更大,(46) = 4.31,< 0.001, Cohen’s= 1.27, 差异的95% CI为[13, 36]。正确返航距离的主效应在符号角度误差上也显著,(2, 88) = 13.65,< 0.001, η= 0.24。被试在正确返航为5米(40 deg)、10米(39 deg)、15米(13 deg)时均高估了转向,s > 3.35,s < 0.01, Cohen’ss > 0.99。这种高估转向的倾向在正确距离为5米或10米时比15米时更大,s > 4.81,s < 0.001, Cohen’ss > 1.41, 差异的95% CI分别为 [13, 41]和[13, 39], 而正确距离为5米和10米时这种高估的趋势差异不显著,(46) = 0.15,> 0.99。其他主效应或交互作用均不显著,s < 0.97,s > 0.43。

图4 正相关信念组和负相关信念组在符合和违背预期条件下的平均位置误差和反应时

图5 不同路段个数和正确返航距离的外出路径的平均符号距离误差和符号角度误差。
为了解释路段个数与相关性信念在符号距离误差数据上的交互作用, 我们合并了不同正确返航距离的数据, 然后对每种路段个数进行了相关性信念的简单效应分析。当外出路径包含4个路段时, 相关性信念的主效应不显著,(2, 44) = 2.29,= 0.11。当外出路径包括8个路段时, 相关性信念的主效应显著,(2, 44) = 6.22,= 0.004, η= 022。正相关信念组(10.2 m)和无相关信念组(3.0 m)均高估返回距离,s > 3.70,s < 0.01, Cohen’ss > 1.91, 而且前者的高估倾向更略为明显,(30) = 2.13,= 0.06, Cohen’s= 0.80, 差异的95% CI为 [0.3, 12.5]。负相关信念组则没有表现出显著的高估倾向,(14) = 0.78,= 0.45。
为了解释路段个数与正确返航距离在符号距离误差数据上的交互作用, 我们合并了三组被试的数据, 然后对每种路段个数进行了正确返航距离的简单效应分析。当外出路径包括4个路段时, 正确返航距离的主效应显著,(2, 92) = 75.26,< 0.001, η= 0.62。被试在正确返航距离为5米时高估距离(4.4 m),(46) = 6.25,< 0.001, Cohen’s= 1.84; 在正确返航距离为15米时低估距离(−2.3 m),(46) = 2.67,= 0.01, Cohen’s= 0.79; 而在正确返航距离为10米时(1.3 m)表现出高估的趋势但没有达到显著水平,(46) = 1.78,= 0.08。当外出路径包括8个路段时, 正确返航距离的主效应显著,(2, 92) = 154.49,< 0.001, η= 0.77。被试在正确返航距离为5米(9.8 m)和10米(5.3 m)时高估距离,s > 4.25,s < 0.001, Cohen’ss > 1.25, 而且在正确返航距离为5米时这种高估的趋势更大,(46) = 6.99,< 0.001, Cohen’s= 1.02, 差异的95% CI为 [3.2, 5.7]; 被试在正确距离为15米(0.0 m)时则没有表现出显著的高估,(46) = 0.02,> 0.99.
3.4 预期对路径完成系统误差的影响
和前文中对于路径完成准确性的分析一样, 我们也对正相关信念组和负相关信念组在正确返航距离为5米和15米时的符号距离误差和符号角度误差数据进行了重新编码、合并。结果如图6所示, 误差线表示标准误。我们对这些数据进行2(路段个数:4或8) × 2(预期:符合或违背)的重复测量方差分析。路段个数的主效应在符号距离误差上显著,(1, 30) = 9.58,= 0.004, η= 0.24, 表明被试在外出路径包括8个路段(5.6 m)时比4个路段(1.9 m)时更显著地高估距离。对于符号角度误差而言, 路段个数的主效应显著,(1, 30) = 6.45,= 0.017, η= 0.18, 但预期与路段个数的交互作用也显著,(1, 30) = 22.06,< 0.001, η= 0.42。其他主效应或交互作用均不显著,s < 0.34,s > 0.56。
为了解释路段个数与预期在符号角度误差上的交互作用, 我们对预期情况进行了路段个数的简单效应分析。被试在符合预期时对包括4个路段(27 deg)和8个路段(19 deg)的外出路径均高估了转向,s > 2.37,s < 0.03, Cohen’ss > 0.86, 但是高估的程度彼此相当,(1, 30) = 0.46,= 0.50。在预期违背时, 路段个数的主效应显著,(1, 30) = 24.85,< 0.001, η= 0.45。被试在外出路径包括8个路段时高估转向(53 deg),(30) = 6.73,< 0.001, Cohen’s= 2.46, 而在外出路径包括4个路段时则不存在这种倾向 (−1 deg),(30) = 0.09,= 0.93。
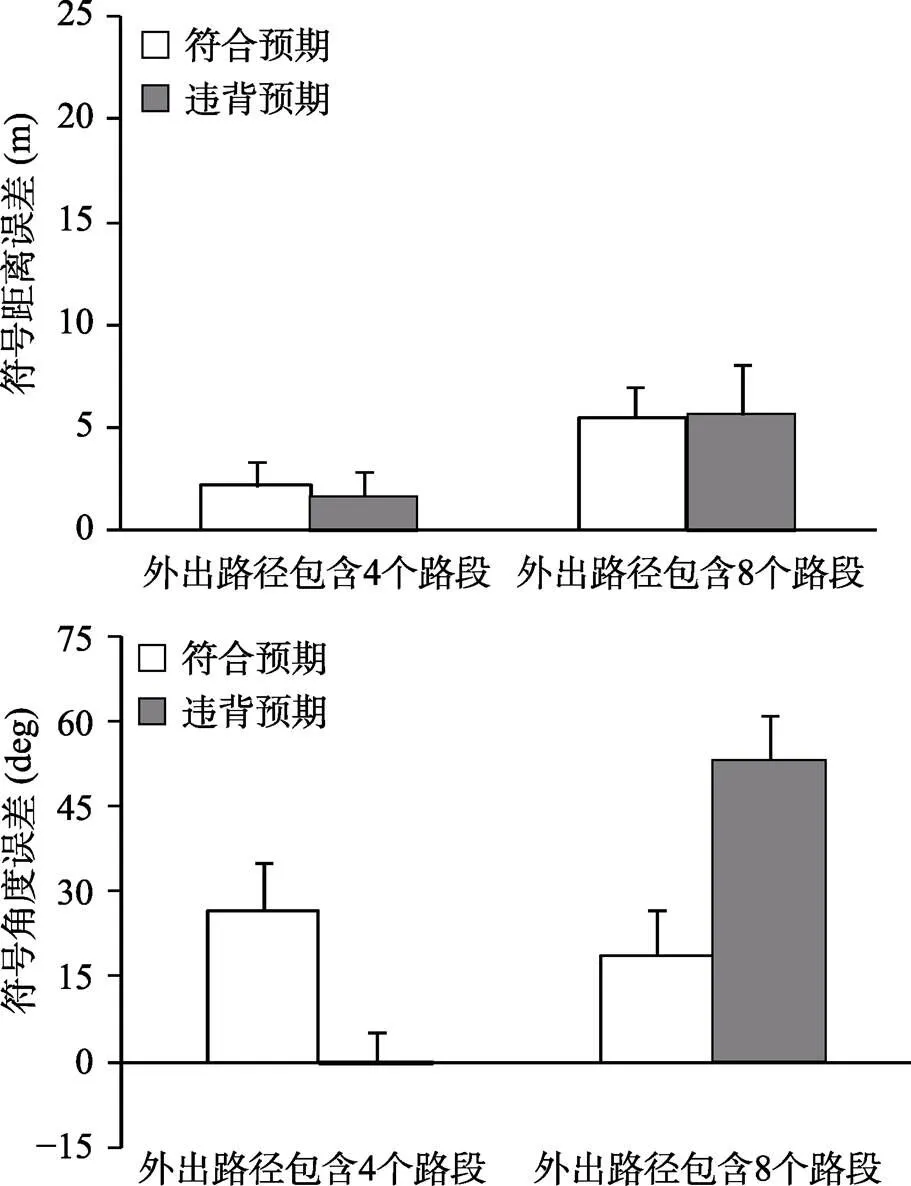
图6 正相关信念组和负相关信念组在符合和违背预期条件下的平均符号距离误差和符号角度误差
4 讨论
4.1 预期对路径整合的影响
本研究通过在实验开始前给予关于路段个数与正确返航距离之间相关性的指导语, 操纵了被试对正确返航距离的预期。组内比较的结果表明, 被试返回起点的准确性在实际情形违背预期时比符合预期时更低, 支持本研究的假设一。组间比较的结果表明, 正相关信念组在经过8个路段后比负相关信念组表现出更大的位置误差, 部分支持本研究的假设二。将组间比较和组内比较的结果结合起来看, 如果个体预期经过的路段越多则与距离起点的距离也越远(即持有正相关信念), 则个体面对复杂的外出路径时会高估的路径整合的错误就会增加。本研究分析系统误差的结果表明, 被试在正确返航距离较小时容易高估返航距离, 而在正确返航距离较大时有可能会低估返航距离, 这与前人的研究结果是一致的(Loomis et al., 1993)。但是, 正相关信念组在面对正确返航距离很大的复杂外出路径时, 仍会表现出显著的高估距离倾向, 这可能是他们路径整合错误增加的主要原因。
这一研究结果体现了非感知觉因素对于人类路径整合的影响, 而这些非感知觉因素不仅包括本研究探讨的预期, 也包括文献中已涉及的记忆(Philbeck & O’Leary, 2005)、先前经验(过继成思, 宛小昂, 2015)、对目标的预知(过继成思等, 2019)、选路策略(Guo et al., 2019)等因素。关于空间巡航中贝叶斯知觉(Bayesian perception)的研究也表明, 巡航者可以把不同来源的信息进行整合并给予不同的权重, 当不同的线索之间差异较小时将结合这些线索做出空间判断, 而在不同的线索之间差异较大时则只依赖其中一种线索(Cheng, Shettleworth, Huttenlocher, & Rieser, 2007)。个体对于未来将要发生的情况的预期并不一定得到现实的验证(Loewenstein & Schkade, 1999), 而且个体对预期与实际情况之间差异的认识影响了人们的认知加工(Hovland, Harvey, & Sherif, 1957), 当实际体验与预期差异较小时个体有可能会将体验向预期进行同化(assimilation), 而在二者差异较大时个体才有可能意识到自己的预期已经被打破了, 并且预期与实际情况并不相符合。因此, 本实验中存在的一种可能性是, 当外出路径包含的路段较少时(即4个路段), 个体可能会通过一定的试次, 例如正相关信念组在体验了几次包含4个外出路段但是正确返航距离特别长(15米)或负相关信念组在体验了包含4个外出路段但是正确返航距离特别短(5米)之后, 而意识到自己对于正确返航距离的预期已经被反复打破, 并因此就不再依赖预期作出行为反应。相较而言, 当外出路径包含的路段较多时, 如此复杂的任务带来的工作记忆负载可能使个体很难意识到预期已被反复打破, 而返回起点的行为也因此更多地受到预期的影响。
另一方面, 如果个体预期经过的路段越多则与距离起点的距离反而越近(即持有负相关信念), 则个体在面对包括8个路段的复杂外出路径时没有表现出对于距离的高估倾向, 表现出比正相关信念组更好的路径整合成绩; 但是这种组间差异在外出路径包含4个路段时并不显著, 这样的结果并不支持我们的研究假设三。一种可能性是, 这种由实验指导语操纵而产生的预期与负相关信念组基于日常生活经验而产生的预期背道而驰, 相互抵消; 而另一种可能性是, 在任务开始前给予负相关的指导语就可能已经打破了他们基于日常生活经验而产生的预期, 使他们在实验中较少依赖预期做出反应。而无相关信念组的被试在实验前就已经被明确告知实验中的路段个数与正确返航距离无关, 这是最符合实验的真实情况的。但是, 无相关信念组在路径完成任务中的表现并没有显著优于另外两组被试, 而且和另两组被试一样受到路段个数和正确返回距离等外出路径特点的影响。这样的结果与我们的研究假设四并不一致, 说明感知觉因素和非感知觉因素均会对路径整合产生影响, 即使持有符合事实的预期也无法消除感知觉因素对路径整合的影响。
4.2 路段个数对路径整合的影响
本研究的结果也表明, 外出路径所包括的路段个数的增加会损害被试返回起点的准确性, 但不影响被试的反应时。当外出路径包含的路段从4个增加至8个时, 被试返回起点的位置误差增加, 符号距离误差减小, 符号角度误差增加, 而反应时没有发生显著的变化。值得注意的是, Wan等(2013)的实验二采用包含4或8个路段的外出路径并将正确返航距离设置为3、6或9米, 结果表明路段个数增加时, 位置误差随之增加, 符号距离误差减小, 而反应时和符号角度误差不受影响。两个研究关于位置误差、符号距离误差、反应时的结果一致, 而符号角度误差上的结果则不一致。本研究与该实验中, 被试均依赖于光流来估计自身的直线前进, 而结合光流和身体感觉信息来估计自身的转动, 但是该实验采用的是视角更大、沉浸感更高的虚拟立方体(virtual reality cube), 而本实验采用的是头盔式虚拟现实, 这种差异也许是符号角度误差结果上有差异的根源之一。两个研究的结果一致表明了外出路径的路段个数对基于内外部自身运动信息的路径整合的影响。
路段个数的增加而反应时并不增加, 表明被试可能在途径外出路径的同时就以在线加工的方式连续地更新了自身与起点之间的空间关系, 而不是等最后到达外出终点时再计算起点的方向及距离自己终点的距离。这里需要指出的是, 为了进行路径完成任务, 个体可以建立以自身为参照系的空间表征并以此为基础进行非结构式的空间更新(nonconfigural updating), 也可能建立以环境为参照系的空间表征并以此为基础进行结构式的空间更新(configural updating), 而这两种类型的空间更新都可以支持路径整合的进行(He & McNamara, 2018; Wiener, Berthoz, & Wolbers, 2011)。在非结构式的空间更新中, 人们在运动的过程中一直跟踪记录自身与外出路径起点之间的空间关系, 而这一过程并不一定需要对外出路径建立详细的内部表征(Wan, Wang, & Crowell, 2012)。相较而言, 结构式的空间更新则需要个体对外出路径进行详细的内部表征(Klatzky, Loomis, & Golledge, 1997)。
但是, 对于复杂的外出路径建立并保持内部表征非常困难, 对工作记忆的要求也非常高。从图1所示的外出路径例图可见, 本研究中空间环境的复杂多变性导致整个外出路径的路型(configuration)可能是巡回曲折的, 行经这样的路径就好像是在“兜圈子”, 而且经过的路段个数多并不一定意味着距离起点的距离就会更远。对于复杂的外出路径, 连续地进行非结构式的空间更新可能是一种更为经济的方式(宛小昂, 2016)。采用这种非构型式的空间更新, 允许人们可以不对行经的路线进行内部表征、不必确认当前的具体位置, 而仍然好似“迷途知返”一般从当前的位置返回整个行程的起点。
当然, 本研究也存在一些值得探讨的问题。首先, 本研究通过指导语而操纵被试对于正确返航距离的预期, 但是无法排除被试因需求特征等因素而不一定被指导语所左右。未来研究也可探讨被试基于时间的预期(如“出发的时间越长而距离起点的距离就越远”)对路径整合的影响。第二, 当Wan等(2013)要求被试在虚拟立方体中进行路径整合时, 即使外出路径包含12个路段, 被试仍然可以更新自身与起点之间的空间关系; 而过继成思等(2015, 2019)采用头盔式虚拟现实的研究表明被试在包含5个路段的外出路径上也可以进行路径整合。相比之下, 本研究将外出路径的复杂程序进一步提高到8个路段, 任务难度较大, 导致被试返回起点时的位置误差也比较大, 尤其是当正确返航距离为5米时非常明显地高估了该距离。但是, 本实验的结果表明被试仍然可以在一定程度上对空间关系进行更新。第三, 本实验中被试依赖于光流来估计自身的直线前进而结合光流和身体感觉信息来估计自身的转动, 因此将本研究的结果推论至其他类型的路径整合则需要谨慎, 其他空间巡航任务中的预期效应也需要进一步的研究来验证。
总而言之, 本研究的结果表明了期望对路径整合的影响, 揭示了人类路径整合的高度适应性和策略性。未来研究可进一步探索预期等非感知觉因素影响视觉路径整合的神经机制, 尤其是空间巡航任务中个体对预期违背事件的认知加工是否仍与纹状体结构有关(D’Astolfo & Rief, 2017; Garrison et al., 2013; Huang et al., 2019)。未来研究亦可探讨预期如何影响空间巡航任务中认知资源的分配, 检验工作记忆对这类预期效应的影响并探讨个体差异(Arnold, Burles, Bray, Levy, & Iaria, 2014)。
Arnold, A. E. G. F., Burles, F., Bray, S., Levy, R. M., & Iaria, G. (2014). Differential neural network configuration during human path integration.,, 263.
Cheng, K., Shettleworth, S. J., Huttenlocher, J., & Rieser, J. (2007). Bayesian integration of spatial information.(4), 625−637.
Chrastil, E. R., Sherrill, K. R., Hasselmo, M. E., & Stern, C. E. (2016). Which way and how far? Tracking of translation and rotation information for human path integration.(10)3636–3655.
D’Astolfo, L., & Rief, W. (2017). Learning about expectation violation from prediction error paradigms: A meta-analysis on brain processes following a prediction error.,, 1253.
Ellmore, T. M., & Mcnaughton, B. L. (2004). Human path integration by optic flow.(3), 255−272.
Garrison, J., Erdeniz, B., & Done, J. (2013). Prediction error in reinforcement learning: A meta-analysis of neuroimaging studies.,(7), 1297–1310.
Guo, J. C. S., Huang, J. P., & Wan, X. A. (2019). Influence of route decision-making and experience on human path integration., 66–72.
Guo, J. C. S., Huang, J. P., & Wan, X. A. (2019). The influence of target knowledge on path integration.,(2), 188–195.
[过继成思, 黄建平, 宛小昂. (2019). 目标预知对路径整合的影响.(2), 188–195。]
Guo, J. C. S., & Wan, X. A. (2014). Psychological and neural mechanisms of human path integration.494–498.
[过继成思, 宛小昂. (2014). 人类路径整合的心理机制与神经基础.(2)494–498。]
Guo, J. C. S., & Wan, X. A. (2015). The effect of learning in virtual path integration.(6)711–720.
[过继成思, 宛小昂. (2015). 虚拟路径整合的学习效应.(6)711–720。]
He, Q., & McNamara, T. P. (2018). Spatial updating strategy affects the reference frame in path integration.,(3), 1073–1079.
Hovland, C. I., Harvey, O. J., & Sherif, M. (1957). Assimilationand contrast effects in reactions to communication and attitude change.(2), 244–252.
Huang, J., Wang, F., Sui, J., & Wan, X. (2019). Functional and structural basis of the color-flavor incongruency effect in visual search.,, 66−74.
Kearns, M. J., Warren, W. H., Duchon, A. P., & Tarr, M. J. (2002). Path integration from optic flow and body senses in a homing task.(3), 349–374.
Klatzky, R. L., Loomis, J. M., & Golledge, R. G. (1997). Encoding spatial representations through nonvisually guided locomotion: Tests of human path integration., 41–84.
Klatzky, R. L., Loomis, J. M., Golledge, R. G., Cicinelli, J. G., Doherty, S., & Pellegrino, J. W. (1990). Acquisition of route and survey knowledge in the absence of vision.(1), 19–43.
Li, D., & Yang, Z. N. (2015). Spatial navigation: The relationship between landmark learning and path integration.(10)1755−1762.
[李丹, 杨昭宁 (2015). 空间导航: 路标学习和路径整合的关系.,(10), 1755−1762.]
Loewenstein, G., & Schkade, D. (1999). Wouldn’t it be nice? Predicting future feelings. In D. Kahneman, E. Diener E, & N. Schwarz (Eds.),(pp. 85−105). New York, NY, US: Russell Sage Foundation.
Loomis, J. M., Klatzky, R. L., Golledge, R. G., Cicinelli, J. G., Pellegrino, J. W., & Fry, P. A. (1993). Nonvisual navigation by blind and sighted: assessment of path integration ability.,(1), 73–91.
Philbeck, J. W., & O’Leary, S. (2005). Remembered landmarks enhance the precision of path integration.,(1), 7–24.
Riecke, B. E., van Veen, H. A. H. C., & Bülthoff, H. H. (2002). Visual homing is possible without landmarks: A path integration study in Virtual Reality.(5), 443–473.
Sholl, M. J. (1989). The relation between horizontality, and rod-and-frame, and vestibular navigational performance.(1), 110−125.
Wan, X. (2016).Hangzhou: Zhejiang University Press.
[宛小昂. (2016).. 杭州:浙江大学出版社.]
Wan, X., Wang, R. F., & Crowell, J. A. (2010). The effect of active selection in human path integration.(11), 25.
Wan, X., Wang, R. F., & Crowell, J. A. (2012). The effect of landmarks in human path integration.,(1), 7–12.
Wan, X., Wang, R. F., & Crowell, J. A. (2013). Effects of basic path properties on human path integration.(1)79–101.
Wang, R. F. (2016). Building a cognitive map by assembling multiple path integration.(3)692–702.
Wiener, J. M., Berthoz, A., & Wolbers, T. (2011). Dissociable cognitive mechanisms underlying human path integration.(1)61–71.
Wiener, J. M., & Mallot, H. A. (2006). Path complexity does not impair visual path integration.(4), 333–346.
Wolbers, T., Wiener, J. M., Mallot, H. A., & Büchel, C. (2007). Differential recruitment of the hippocampus, medial prefrontal cortex, and the human motion complex during path integration in humans.(35), 9408−9416.
Worsley, C. L., Recce, M., Spiers, H. J., Marley, J., Polkey, C. E., & Morris, R. G. (2001). Path integration following temporal lobectomy in humans.(5), 452−464.
Zhang, T., & Li, S. G. (2011). Neural mechanism of self-motion perception.(10), 1405−1416.
[张弢, 李胜光. (2011). 自身运动认知的神经机制.(10), 1405−1416.]
Zhao, M., & Warren, W. H. (2015). How you get there from here: Interaction of visual landmarks and path integration in human navigation.(6), 915−924.
Zhou, J. S., & Zhang, K. (2005). Kinestheic, irrelevant motion and path integration.(6), 1306–1308.
[周佳树, 张侃. (2005). 运动觉、布局无关运动与路径整合.,(6), 1306–1308.]
Influence of expectations on human path integration
ZHANG Weiwei; HUANG, Jianping; WAN Xiaoang
(Department of Psychology, Tsinghua University, Beijing 100084, China)
Path integration refers to a type of navigation in which navigators integrate information regarding self-motion in order to update the spatial relationship between themselves and the starting point of their journey. Human path integration has been often assessed via a path completion task in which the participants travel along several segments and then attempt to directly return to the origin of an outbound path. Previous research has revealed the influence of non-sensory factors on human path integration, such as memory, previous experience, target knowledge, and route decision-making. It remains unclear, however, how individuals’ expectations regarding the outbound paths influence their return-to-origin behavior.
In the present study, we used head-mounted display virtual reality to present hallway mazes and provided different instructions to 3 groups of participants in order to manipulate their expectations concerning the correct homing distance (i.e., the Euclidean distance between the starting and ending points of an outbound path) before they performed the path completion task. Specifically, the 3 groups were informed that the number of segments of each outbound path was positively correlated, negatively correlated, or uncorrelated with the correct homing distance. In actuality, we used an orthogonal design to make the correct homing distance uncorrelated to the number of segments.
The results revealed that the participants exhibited less accurate return-to-origin responses when their expectations concerning the correct homing distance were violated, compared to when these expectations were confirmed by the actual experiences. When the participants expected the correct homing distance to be positively correlated with the number of segments, they showed even greater errors for more complex outbound paths than those who expected a negative correlation. That being said, it should also be noted that all participants’ return-to-origin responses were subject to the influence of the number of segments and correct homing distance, even though only one group of participants was instructed to have valid expectations.
Taken together, these results demonstrate the influence of expectation on human path integration, although only having valid expectations cannot eliminate the influence of path properties on path integration. Moreover, individuals may rely more on expectation for more complex outbound paths. These findings therefore highlight the important roles that non-perceptual factors play in human path integration, and demonstrate that human path integration is an adaptive and strategic process.
expectation; path integration; spatial navigation; virtual reality
2019-02-25
* 国家自然科学基金项目(31200758)资助。
宛小昂, E-mail: wanxa@tsinghua.edu.cn
B842
10.3724/SP.J.1041.2019.01219
