四点简支等弯矩梁装置对应变计标定精度影响
2019-11-16晏志鹏邓足斌
晏志鹏 邓足斌
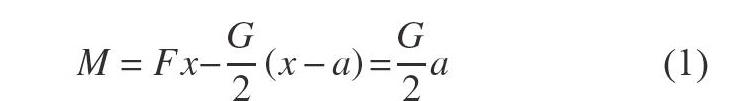

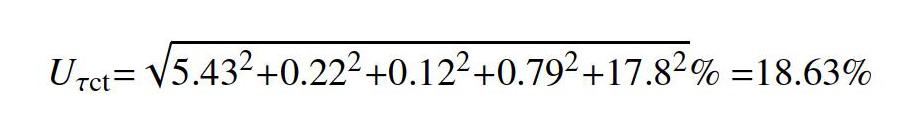
摘要:通过理论分析,分别从加载摩擦力、试验梁尺寸变化和温度变化着手,进行误差计算,四点式简支等弯梁标准应变的不确定度达到18.63%,严重影响应变计性能的标定精度,不符合电阻应变计国家标准和OIML国际RNo.62号建议要求。通过对比分析,高精度SK-IA钢架梁结构可以将误差降低,实现标准应变相对误差仅0.054%,高温下也只有1.2%,有效解决应变计标定精度,实际测试结果也进一步验证该结论。
关键词:等弯矩梁;高温;应变计参数标定;应变标准发生装置;高温灵敏系数;蠕变;漂移
中图分类号:V416 文献标志码:A 文章编号:1674-5124(2019)10-0101-08
0 引言
近70年来,国内外多采用四点简支等弯矩梁和悬臂梁原理制成的应变发生装置,这是受美国宇航标准NAS942的影响所致。等弯矩梁实现起来结构简单,应用广泛,但无人深究工程应用中四点简支等弯矩梁和悬臂梁原理存在较大误差。
收稿日期:2019-01-03;收到修改稿日期:2019-03-11
作者简介:晏志鹏(1974-),男,陕西汉中市人,高级工程师,主要从事应变电测技术和传感器研究。
通信作者:邓足斌(1939-),男,湖南邵阳市人,教授级高级工程师,主要从事应力应变和传感器测试设备及测试方法的研究。
应变计是结构强度测试、疲劳测试、应力分析和寿命评估等的主要测量传感器[1],广泛应用于航空航天、化工、能源等领域。利用应变计可以实现多点和大面积应变测量,应变计的精准测量是研究结构力学性能影响的问题必要手段[1-2]。应变计的特性参数随温度变化,由于环境温度的影响,应变计的指示应变往往与实际相差甚远,甚至不能确定指示应变曲线的真实性[3-4]。灵敏系数、蠕变、零漂等应变计特性参数的准确性,会对真实应变修正带来影响,甚至引入较大误差。究其原因,是应变计的参数标定问题尚未完全解决,应变计标定装置的误差未能明确,从而影响应变测试的精度[5-6]。
结构简单的四点简支等弯矩梁、等强度梁等应变计参数标定测试装置虽然在很多单位得到应用,但应用中存在的问题和误差并没有得到分析和研究。当前,美国NAS942、英国DD6、德国HBM、瑞典FFA、国内清华大学、建筑研究总院、国发606所等国内外单位采用9种不同结构的测量标定装置,可归纳为3种原理4种结构,其中等强度梁等腰三角形对称要求高,制造困难,测量误差大;四点简支等弯矩梁影响因素多,带来较大误差[7]。本文利用砝码加载的四点式弯矩简支梁检定装置和SK-1钢架梁结构装置,分别从原理和实际测试数据对比,对不同温度下的灵敏系数标定误差影响因素进行分析,对应变计的标定有一定的参考意义。
1 四点简支等弯矩梁模型原理
砝码加载的四点式简支梁结构采用两端支点支撑,中间两点加载[2,6],中心点采用百分表或挠度计测量位移挠度,其受力简图见图1。
根据图1,加载砝码重量为G时,支点反作用力F=1/2G,属于绝对挠度弯矩测量法,梁上任一点的弯矩为:
M=Fx-G/2(x-a)=G/2a(1)
根据胡克定律得:
其中:ε——试验梁理论应变量;
δ——试验梁弯曲应力;
E——试验梁弹性模量;
W——试验梁抗弯截面系数,试验梁为矩形截
面,W=Bh2/6。
根據材料力学挠度曲线公式可知弯矩梁中心位置挠度为:
由式(2)、式(3)可得应变与挠度的近似关系:
其中:h——试验梁的厚度;
f——试验梁中间点的挠度值;
L1——试验梁有效长度。
由式(4)得知,试验梁表面应变与试验梁尺寸、加载点位置、支点之间的试验梁有效长度、挠度值有关,但如果是砝码加载,无法做到挠度控制加载,挠度还与弹性模量、砝码重量有关,即弹性模量、珐码重量也会影响试验梁表面应变。
2 四点简支等弯矩梁误差分析
从国外的资料看,多数应变计标定设备都是悬臂梁和砝码加载式四点简支等弯矩梁原理两种结构,国内主要也是砝码加载式四点简支等弯矩梁。所有标准应变的计算均按简图进行理论计算,这与实际情况有较大的出人。为了解决这类问题,想通过实验的方法对实际构件或其模型进行应力应变分析测试,求取其最大应力作为强度计算的依据。实际上花了很大的精力,获得数据的准确度仍然很差,这是因为实验方法得到指示应变修正后,数据仍不准确,这就是四点简支等弯矩梁装置不能准确标定出应变计蠕变、温度蠕变和灵敏系数随温度变化等参数的原因。
2.1 摩擦力系数影响误差分析
四点简支等弯矩梁装置结构上由于两力点与两支承都属于刀口或滚柱支座,只能限制一个方向的运动,加载时或加热时,它们与试验梁表面都存在相对位移和外延,对梁变形有补偿作用,产生摩擦力。常用装置的结构设置如下:试验梁加载点和邻支撑点之间的距离a=85mm,2c=216mm,L=420mm,L1=386mm,B=30mm,梁厚度h=6mm,砝码质量=800kg,梁表面的应变可以根据式(4)计算得出,得到标准应变,以下误差计算均以上述尺寸为参考值。
这里相对运动产生的摩擦力形成标定梁上的轴向力,已构成四点等弯矩梁不可分割的组成部份,摩擦系数极不稳定,随着温度和砝码的变化而变化,无法构成刚性封闭的平面静态力学平衡系统,无法获得准确结果。摩擦力也会随温度不断变大,标定梁表面氧化起皮,氧化层由片状过度到条状,标定梁表面变为凹凸粗糙表面,使摩擦系数都呈现先降后升高的趋势,当温度达到600~1000℃,材料晶体组织结构也会不断变化,塑性变形加剧,使阻力不断加大,高温状态下的复杂变化,很难说清高温状态摩擦系数变化有多大,只能假设数值代人计算,据参考文献[8-9],在1000℃摩擦系数fm最大可达4,所以带来不能允许的相对偶然误差δZT,可由下式求得:
假设常温fm=0.2,高温1000℃时fm=4,标准机械应变1000με,通过下式计算可求得相对标准应变的不确定度UrZT:
从计算结果来看,高温1000℃下标准机械应变的不确定度可以达到5.43%,严重影响灵敏系数随温度变化测量准确度。
四支点的摩擦力形成的轴向力对试验梁表面的应变作用,使一面应变变大,另一面应变变小,这种力在式(4)中无法反映,一般会忽略,这是工程实践中无法真正实现四点等弯矩矩梁原理的原因。摩擦力对试验梁变形理论的干扰作用,使梁表面应变始终处于随时变化的状态,造成电阻应变计的温度灵敏系数、温度系数和蠕变无法测准。从理论上讲,这种有精度要求的标定装置,加载后必须要求成为一元刚性封闭的平面静态力学平衡系统,一个能量守恒系统,其变化能量按式(4)都应反映在试验梁的应变ε上,其实它反映小很多,这就产生了误差,再加上梁表面应变ε的不均匀性造成应变计测试数据的分散。
2.2 四点简支纯弯矩梁尺寸影响误差分析
四点简支等弯矩梁装置,加载机构和支撑点都置于加热炉中,为保证加载方便,受结构限制,试验梁尺寸为420mm×30mmx6mm,做得小而薄,梁的均匀性和精度很差。宽与厚之比值越大,梁表面的应变精度、均匀性按几何级数下降,只就梁宽B和梁厚h之比而言,相对尺寸变化δs引起的相对标准不确定度Urs也比较大。
其中s为梁宽度与厚度之比;μ为试验梁材料的泊松比,一般为0.3;ε为标准应变,一般为1000μm/m。
从计算结果来看,由于试验梁宽度较宽,厚度较薄,其宽厚比对试验梁标准机械应变的不确定度影响达到0.22%。
四点简支等弯矩梁横截面为矩形,理论上是根据矩形梁受等弯矩后,试验梁中轴变形后为一条理想的圆弧线,但实际情况下为一条抛物线[2],因此梁表面的应变值各点只能处于轴对称的相等,并不能保证整个曲面上的应变相等,实际的中性轴抛物线[2]就会带来应变不均匀性δp,由不均匀引起的相对标准不确定度Urp也就相对较大,也对试验梁的标准应变产生影响。
其中z为两个加力点之间距离,标准距离为108mm。
从结果来看,由于试验梁在施加标准应变时,其矩形截面中轴线形成抛物线曲线,在整个弧面应变不均匀,引起的不确定度为0.12%。
标定梁与加载部件构成系统的同一平面,该系统的两个加载力点,两个支撑点理论上相互之间平行,实际上并不能保证其平行性,造成试验梁在加载产生自身扭曲,形成力点结构之间平行性扭矩,会带来形状误差δθ,按扭杆中的纵向应变公式计算,引起的相对标准不确定度Urθ也会有较大数值误差。
其中θ为标定梁上单位长度的扭转角,因梁薄而长,设θ=0.1°。
从计算结果来看,试验梁在施加标准应变时,受加载力点和支撑点不平行,带来的扭曲变形,当单位长度扭转角变化1°时,引起的不确定度为0.79%。
综合以上三项误差,可以得出尺寸方面的相对不确定度为:
2.3 温度对四点简支纯弯矩梁尺寸影响误差分析
高溫炉为追求炉膛的温度均匀性,四点简支纯弯矩梁和加载装置含炉内、炉外两部分,应变计粘贴在试验梁上,试验梁表面温度应均匀,受结构限制,试验梁的温度均匀性很难保证[10]。1000℃时,经过实测,试验梁25mm范围内温度误差△t=15~30℃,就会在试验梁表面形成温度应力和尺寸误差。其引起的相对标准不确定度Urt也是均匀分布在实验梁表面。假设试验梁表面的的温度为1000℃±25℃,则温度差值δ(△t)=25℃。
从结果来看,由于试验梁温度不均匀性,在同一温度下的温度阶梯引起的不确定度可达1.44%。
最大的误差源由弹性模量的变化引起,占总误差的99%以上,高温下标准载荷应变的不确定度为Uεt沿标准梁表面均匀分布。
2.3.1 高温下试验梁载荷应变对灵敏系数测试的影响
高温下,采用砝码加载的四点式简支弯矩梁对灵敏系数测试时,试验梁的应变与弹性模量E和试验梁外形尺寸变化相关。根据简支梁力学模型式(2),试验梁形状和弹性模量引起的误差相当于对式(20)进行全微分,即
式中:Va——高温下砝码加载点和支点之间距离的变化量;
VB——高温下试验梁宽度的变化量;
Vh——高温下试验梁厚度的变化量;
VE——试验梁弹性模量高温下的变化量;
VG——砝码加载力的变化量。
将高温应变计用自研高温陶瓷胶G-1000粘贴到GH128高温合金简支试验梁上测试灵敏系数,试验梁的弹性模量、外形尺寸会发生变化,对应变计的输出产生较大影响。当温度为1000℃时,通过表1、表2可知,试验梁的线膨胀系数从11.3×10-6/℃变化到16.3×10-6/℃,变化量为5.0×10-6/℃;弹性模量从208GPa变化到144GPa,变化量为-64GPa;试验梁泊松μ=0.3;砝码不变化,温度带来加载杆与试验梁之间微小的角度误差很小,不考虑此影响。因此其综合误差为:
2.3.2 温度带来的其他影响误差
四点式简支等弯矩梁装置采用绝对测量法,挠度测量仪表通过绝热杆接触试验梁上测其变形挠度,时间长一点,梁上热量就会通过绝热杆传到测挠度的仪表上,影响仪表的读值的真实性,带来较大读数误差,影响实际载荷应变量。
四点式简支等弯矩梁原理装置采用砝码单向加载,高温下试验梁回弹性较差,无法回到原始状态,这是试验梁弹性后效及徐滑效应(即高温下塑性变形)带来的影响,实际上无法进行计算。
四点式简支等弯矩梁原理装置采用砝码单向加载,是一种恒力向下长时间吊挂加载,在恒力的作用下必然产生正蠕变,其作用会消除应变计的负蠕变,使被测应变计蠕变测不准确。且不能实现正反两个方向加载,方向性误差不能自动消除,该误差大于0.2%,高温下影响更大。
每次贴片前都必须打磨标定梁,使梁变薄,珐码是恒定的,则应变就会慢慢变大。标定梁更换材料,弹性模量会发生变化,在砝码恒定加载下,梁上产生的应变又会变化。在高温条件下,弹性模量是一个温度段中的平均值,也会带来误差。还有线膨胀系数等都需要修正,这样的变化状态无法确定测试的不确定度。
除了上述误差源以外,还有参考资料[3,11]中的10多项具体误差无法计算核实,会对整个测试带来巨大影响。综合摩擦力影响、试验梁尺寸误差影响和温度的影响,可以得出四点简支弯矩梁装置的相对不确定度约为:
3 解决方案
四点式简支等弯矩梁原理装置误差大,从结构上无法消除前述很多影响因素,與电阻应变计国家标准[12]和OIML R No.62建议规定的精度0.2%要求相差甚远,不可能准确测量中高温应变计的灵敏系数随温度变化、蠕变。据资料,欧洲DD6标准和德国H公司的位移加载的四点简支弯矩梁装置,其试验梁是25.4mm×25.4mm正方形,长约1000mm,采用8个滚珠轴承,实现正反位移加载,在常温下可以将应变计性能准确标定[6],而中高温下也还存在摩擦力,尺寸误差等影响,会对温度下的性能标定产生影响,具体影响度应该小于目前国内砝码加载的薄梁四点简支弯矩梁装置,本文不做分析。
3.1 SK-1纯弯矩钢架梁优缺点
解决四点简支弯矩梁装置较大的误差影响,可以采用高精度SK-1A钢架梁式应变计参数测定装置实现。根据文献[3,11],SK-1常温下的相对误差约为0.054%,高温下约为1.2%,相对于四点简支弯矩梁装置误差很小,具体对比详见表3。
DZB-SKIA应变计参数测定装置是位移加载后形成刚性封闭的静态力学平衡系统,避开了标定梁材料弹性模量随温度变化而变的影响,采用新的相对测量法,能够准确测量高温下灵敏系数、灵敏系数随温度变化、蠕变等应变计参数。
3.2 SK-1纯弯矩钢架梁装置原理
纯弯矩钢架梁采用两端高刚度(刚性)力臂开合带动试验梁弯曲变形,中心点采用高精度三点挠度计(拉线)测量位移挠度,并控制力臂开合度,以保证试验梁中心点挠度达到准确值[3,6]。其受力简图见图2。
根据图2,刚性力臂端头施加δ力值(δ+、δ-),试验梁两端的弯矩属于纯弯矩,梁上任一点的弯矩为:
M =σa(6)
根据胡克定律,可得纯弯矩梁表面的应变为:
其中,ε±为试验梁应变量;σ为试验梁弯曲应力;E为试验梁弹性模量;W为试验梁抗弯截面系数,试验梁为矩形截面,W=Bh2/6。试验梁还受一对非常小的轴向力的影响,在实际应用中应考虑,因此,试验梁表面的凸、凹应变为:
根据三点式挠度法测得的纯弯梁凸、凹应变与试验梁中心位置的挠度f之间的关系为:
式中:h——试验梁的厚度;
f——试验梁中间点的挠度值;
a——力臂长度;
c——三点挠度计安装支点距离的一半;
μ——试验梁的泊松系数。
采用三点挠度计挠度值控制试验梁的加载,试验梁的表面挠度只与试验梁的厚度、三点挠度计安装支点的距离、泊松系数和应变量有关,当应变量、试验梁厚度,三点挠度计支点距离确定,也就确定了其挠度值,与试验梁的弹性模量无关,与加载力大小无关。纯弯矩钢架梁可以产生凸凹交变加载,可以连续迅速加载,加载到位可以迅速读取数据,测量值中不会引入蠕变,加载也不存在任何冲击。
高精度DZB-SK1A装置上实现配置中温炉、高温炉,试验梁在炉中加热,只需考虑试验梁的误差即可。为保证炉内的温度均匀,设置隔热保温,在温度20~1000℃时,中央120mm范围内,温度均匀性优于±0.8%。高温炉内,三点挠度计测挠度控制应变的方式会存在问题,以钢架梁两力臂刀座上作用力中心点,安装拉线位移传感器测量刀座之间的相对位移,与三点挠度计作比对,测出两刚性铰夹持试验组合梁的实时理论值和相对变化,这样可以克服引入误差,准确比对出位移与三点挠度计的对应关系,实现等效精度的机械应变值,分辨率提高18~20倍,达到同一精度级,解决高温精确应变加载的目的。
3.3 SK-1纯弯矩钢架梁装置灵敏系数随温度变化标定结果
为了验证SK-1标定的准确定,利用SKI钢架梁装置对中航电测(ZEMIC)和美国V公司生产的应变计测试了灵敏系数随温度变化dk性能,具体结果见表4。
由表可知,美国V公司的常温电阻应变计J2A-13-S227K-350(BATCH NUMBER:E416344)和J2A-13-S047C-350(BATCH NUMBER:E416348)包装标注的灵敏系数随温度变化均为:1.30±0.2%/100℃,采用SK-1钢架梁装置重新将它们与中航电测对应型号的应变计进行对比测试标定,J2A-13-S227K-350测定结果为dk=1.331±0.206%/100℃,两者近似相同,但J2A-13-S047C-350测定结果为dk=0.86±0.206%/100℃,与包装标注指标相差较远。为了保证测试准确性,又采用不同机械应变量和不同输出仪表测试,每天测试一次,共测试4次,测出的结果都是dk=0.86±0.208%,其他应变计测试数据也相同,结果稳定,其实测dk值与包装标示值不一致。
为了使测试结果更加准确,又同时测试了热输出和灵敏系数在不同温度下的相对变化,如图3、图4所示,从结果来看也能验证其dk值的准确和可靠。
从曲线来看,V公司的热输出曲线和灵敏系数在不同温度下的变化曲线基本趋势与中航电测一致,只是J2A-13-S047C-350的相对Kt/K5在80℃的数值相对小一点(也全部超过100%,与康铜敏感栅的灵敏系数趋势一致),导致dk值偏小,但确实与包装标示相差较大,由于不清楚V公司采用何种标定装置进行测试,是测试装置带来误差还是其他原因,无法确定。
3.4 高温下不同试验梁结构标定灵敏系数随温度变化的实际数据
根据前述分析,采用高温应变计TG350-3AA900-YF50框架式裸栅应变计(如图5所示),和G-900高溫陶瓷胶粘贴,试验梁采用GH128高温合金,分别测试砝码加载的四点式简支梁结构和SK-1纯弯矩钢架梁结构随温度变化的灵敏系数(即温度灵敏系数Kt和常温灵敏系数Kr的比值Kt/Kr),具体数据如表5所示和曲线示意图如图6所示。
通过以上数据和曲线,结合前述分析,高温应变计灵敏系数随温度变化测试均会存在测试误差,虽然数据和曲线趋势相似,但相对而言,纯弯矩钢架梁结构测量误差最小,也最接近于真实数据。
4 结束语
通过理论分析和实际测试,确定了四点简支等弯矩梁装置标定应变计灵敏系数主要误差源,对误差源进行了分析。对于有精度要求的应变计参数标定设备,不能采用砝码加载四点简支弯矩梁原理装置,其误差源太多,不确定度高达18.63%。
对于有精度要求的应变计参数标定设备,加载后一定要成为一元刚性封闭的平面静态力学平衡系统。对于高温下的应变计灵敏系数、蠕变、线性和灵敏系数随温度变化的测试标定,应采用配置的专用加温炉SK-1A钢架梁式应变计参数测定装置。
参考文献
[1]尹福炎.瞬态加热条件下高温应变计测量误差的修成方法[J].强度与环境,2005(1):32-36.
[2]王文瑞,张佳明,聂帅.高温应变接触式测量精度影响因素研究[J].固体火箭技术,2015,38(3):439-444.
[3]邓足斌,郑振洲.高精度钢架梁式SK-1应变计参数测定装置的结构和精度评定田.仪表技术与传感器,2001(1):38-41.
[4]王文瑞,张佳明,闫晓强,等.高温应变片关键参数标定方法[J].工程科学学报,2015,37(12):1645-1650.
[5]邓足斌.应变计灵敏系数测定装置中标定梁的优化设计[J].仪表技术与传感器,1998(1):11-14,1998(2):11-13
[6]邓足斌.SK-1应变计灵敏系数测定装置的方案及主要机构的选择[J].传感器技术,1987(1):56-61.
[7]叶迎西,孙天贺,艾延延.温度对电阻应变片测量精度影响的仿真研究[J].沈阳航空航天大学学报,2013,30(2):27-30.
[8]RECHARDS W L.A new correction techniques for straingauge measurements acquired in transient-temperatureenvironments[R],1996.
[9]MA L C,WU T T,ZHAO L B.Development of tempera-turecompensated resistance strain gages for use to 800℃[C]//Inproceedings of the international conference on experimentalmechanics,1985.
[10]邓足斌.电阻应变计灵敏系数Ki及其应变值εi计算公式的分析[J].传感器技术,1986(1):49-54.
[11]邓足斌.纯弯矩梁型应变计灵敏系数测定装置的误差分析和精度评定方法[J].传感器技术,1999(7):10-12.
[12]金属粘贴式电阻应变计:GB/T13992-2010[S].北京:中国质检出版社,2010.
(编辑:商丹丹)
