超声纵横波螺栓载荷在线检测方法研究
2019-11-16李栋朱晓磊陆晓峰
李栋 朱晓磊 陆晓峰


摘要:针对传统扭矩法控制螺栓载荷误差过大的问题,提出使用超声纵横波法来进行螺栓载荷的检测方法。基于声弹性定理,建立螺栓应力与超声纵横波声时关系的螺栓载荷预测理论模型,避免螺栓原始长度的测量,真正实现无损检测。通过制定实验表征方法,设计磁力探头夹具,建立超声横纵波测螺栓载荷的实验平台,保证每次测量数据的稳定性与测量位置的一致性。对8.8级高强度双头螺栓轴向力进行实验验证,并结合理论模型获得声弹性系数。结果表明:螺栓的轴向应力与超声纵横波声时为线性关系,实验值与理论计算值在100~600MPa的最大误差小于5.61%,误差绝对值的平均值在2%左右。
关键词:螺栓载荷;纵横波法;测试理论;声时
中图分类号:TH131.3;TB559 文献标志码:A 文章编号:1674-5124(2019)10-0040-05
收稿日期:2018-08-27;收到修改稿日期:2018-09-29
基金項目:国家自然科学基金(11772147);江苏省高校自然科学基金(16KJB130003)
作者简介:李栋(1994-),男,山东济宁市人,硕士研究生,专业方向为超声波测螺栓载荷技术。
0 引言
螺栓松动失效是螺纹联接常见的失效形式。接触表面的材料相互嵌入、材料蠕变、预紧力不够、摩擦系数的变化等因素,都会导致螺栓的夹紧力下降,尤其是在振动冲击或高温环境下,更容易发生松动。同时,设备的高参数化、紧凑化、轻量化使得螺栓载荷检测方法必须满足占用空间小、快速、精确等优点。现有的扭矩扳手法、光弹法等已无法满足现场的需要,亟需一种新的测试方法。
超声检测以其快速、直观、准确等优点,被广泛应用于壁厚检测、内部缺陷检测、螺栓载荷检测以及残余应力检测。S.OKA[1]首个发现了超声波的双折射现象,开辟了超声波测应力的先河。日本学者德冈辰熊[2]从有限弹性理论出发,求解出超声横波沿主应力方向传播速度差与主应力差的关系,为现代超声波测量螺栓载荷奠定了理论基础。之后冉启芳等[3-4]基于声弹性理论,在实验室条件下,利用纵波两次回波的时间间隔测定螺栓载荷,并对形状因子进行了试验研究。刘镇清等[5]研究了碳钢的纵横波声时与应力、温度的关系,并初步研制了螺栓载荷测量仪。江泽涛等[6-7]创立一种纵横波相结合测螺栓应力的方法,虽然对温度补偿也做了实验并总结了规律,但是未给出详细的应力系数,仅限于实验室研究方法。张俊[8]贾雪等[9]详细论述了基于声弹性理论的超声螺栓应力测量原理,同时研究了温度对波速的影响。徐春广等[10]针对螺栓在低载荷与高载荷不同情况下对测量系数进行了分类讨论。国外学者SUDA M等[11]基于声弹性理论,研制了用于控制火力发电厂涡轮机外壳螺栓的检测系统,将超声波测螺栓载荷的方法应用到了实际工业生产中。综上所述,国内外学者针对超声波螺栓载荷测试方法做了相应的研究,其测试精度均在5%以内,但是,单波测试方法需要了解螺栓零应力下,精确的初始长度才能达到上述精度。同时关于双波法的研究也仅仅局限为规律探讨。
本文就超声波螺栓载荷测量方法存在的不足,探索超声纵、横波与螺栓应力之间的关系,建立基于超声纵横波的螺栓载荷测试方法,并通过实验对该方法进行了验证,得出螺栓材质的应力系数。
1 螺栓轴向力检测理论模型
1.1 初始声速计算模型
根据声弹性力学可知,零应力状态下超声波在金属中传播的声速与金属材料的二阶拉曼常数(λ、μ)和螺栓材料密度(ρ)有关,超声纵波声速VL0和横波声速VS0可由以下公式计算:
1.2 理论模型
当螺栓处在某应力状态下时,超声波在其中传播的速度会受到影响,不同的波受影响程度不同,即有应力时,超声纵波声速VL和横波声速VS可由下式计算:
VL=VL0(1+k'Lσ)(1-α△t)(3)
VS =VS0(1+k'Sσ)(1-α△t)(4)
式中:k'L、k'S——超声纵波与横波在介质中的声弹性系数;
α——超声波速温度系数;
△t——温度改变量。
超声波测试螺栓载荷的原理是基于螺栓应力对超声波声速的影响,测量载荷作用下螺栓伸长量所对应的声时差,建立声时差与螺栓应力之间的关系,获得螺栓载荷的计算方法。因此,为了提高超声波螺栓载荷测试方法的准确性,需要建立螺栓在服役过程中各部分伸长量与应力和温度之间的关系。螺栓预紧示意图如图1所示。图中L1为螺栓预紧的有效作用范围,与螺栓的直径、螺纹规格等有关,该部分的伸长量受到应力和温度的作用;剩余长度L2=L-L1,该部分的伸长量与温度有关。
当螺栓受到载荷作用时由应力引起的螺栓有效长度段伸长量为:
Lσ=L1σ/E(5)
式中:L1——L1=r+D,r为两螺母间距离(mm),D为螺栓的公称直径(mm);
σ——应力,MPa;
E——弹性模量,MPa。
温度引起的螺栓伸长为:
Lt=Lβ△t(6)其中,β为材料的热膨胀系数。
根据螺栓在预紧工况下各部分伸长量关系,将式(5)和式(6)代入式(3)中,获得超声纵波声时计算公式:
同理,将式(5)和式(6)代入式(4)中,获得超声横波声时计算公式:
对式(7)和式(8),化简可得:
在零应力条件下,超声波声速只受到温度影响,则超声纵、横波声时计算公式为
将式(11)、式(12)分别代入式(9)和式(10),并将两公式相除得:
在测量间隔较短的情况下,温度变化将比较小,基本可以忽略,即△t=0,则式(13)可简化为:k's,则有:
y=1/a-bx(15)
通过式(15)可以发现应力与超声波声时、初始声速和螺栓有效长度之间满足Farazdaghi-Harris曲线形式[12]对式(15)取倒数变换可得线性关系式:
y-1=a-bx(16)
因此,对于不同的螺栓只需要知道其k'L、k'S与L1即可通过测试求得其应力。由于模型中消除了螺栓初始长度对计算结果的影响,该模型同样可以用于已安装或不方便测量原始长度螺栓的载荷检测与计算。
2 试验方法
试验选用3根经过调质处理的8.8级35CrMoA高强度螺栓作为试样,两端面经过线切割保证平行度公差在7~8级,经打磨保证粗糙度优于Ra3.2。螺栓材质成分检测结果如表1所示,符合35CrMoA的主要成分组成。
使用MTS 311.32试验机,设计螺栓拉伸工装夹具,模拟螺栓预紧工况[13]如图2所示。超声波测试装置使用OLYMPUS 38DL PLUS超声波测厚仪,纵、横波探头中心频率为5MHz,探头直径6mm,准确度可达0.001mm,如图3(a)所示(探头为两个,分别是横波探头与纵波探头)。为了保证每次测定的位置以及探头压紧力保持一致,设计如图3(b)所示的磁力与弹簧组合的夹具。探头与夹具安装在螺栓头端部,通过磁铁与螺栓形成良好的贴合。
试验施加的载荷控制在螺栓材料的弹性范围内,对于8.8级的螺栓屈服强度可达640MPa。本次试验加载区间为100~600MPa,加载步长50MPa,加载速度1MPa/s。
3 结果讨论
超声纵、横波测试的声时与应力之间的关系如图4所示。可以看出,声时与应力成直线关系,满足材料线弹性力学行为。
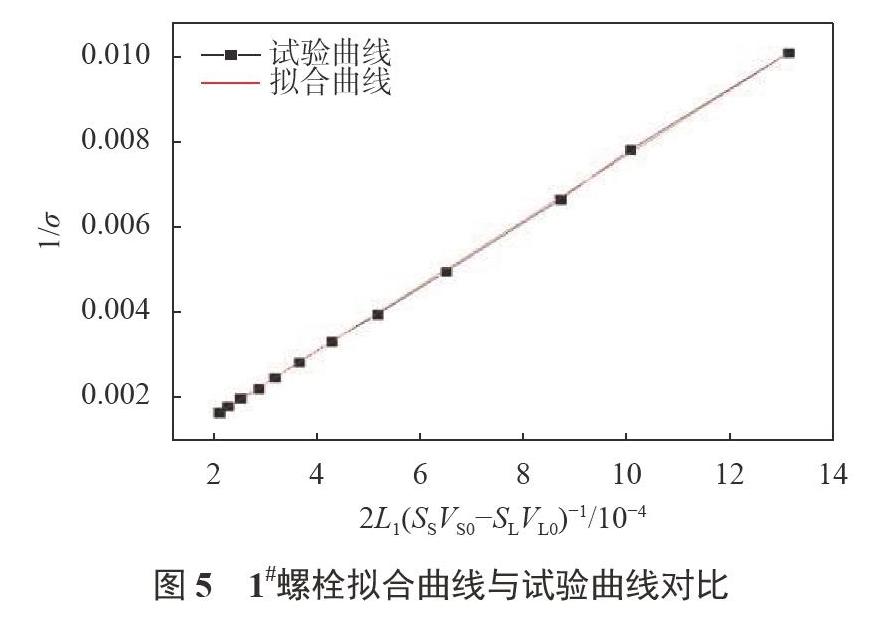
根据式(16),将L1=169.3774mm的实验数据进行拟合,获得超声纵、横波声弹性系数,k'L、k'S,拟合结果与试验结果对比如图5所示,拟合参数如表2所示。从图5可以看出,拟合结果与试验结果曲线趋势一致,结合表2可知,其拟合度达到r2=0.99991。根据表2所示声弹性系数,将L1=162.113mm和L1=136.0018mm的测量数据代入式(16),计算得到应力值与实测值对比,如图6所示,误差见表3和表4。
从表3与表4可以看出,L1=162.113mm和L1=136.0018mm两根螺栓在100600MPa应力下的误差大都集中在5%以内,L1=162.113mm的螺栓最大误差为4.08%,L1=136.0018mm的螺栓最大误差为5.61%。两根螺栓校核误差绝对值的平均值分别为1.99%和1.%%,证明模型是正确的。
4 结束语
本文建立了超声纵、横波螺栓载荷计算模型,在此基础上对8.8级高强度螺栓进行了试验验证。结果表明,材质为35CrMoA的螺栓经调制后,超声纵波声弹性系数为-833×10-5,超声横波声弹性系数为-3.597×10-5;经过实验验证,在100~600MPa,两组应力预测结果的最大误差为5.61%。两组验证结果误差绝对值的平均值分别为1.99%与1.96%,远远小于传统扭矩法的误差,可应用于航空航天、石油化工、船舶汽车等领域的紧固件预紧与检测,同时也能解决已经安装的紧固件载荷检测问题。
参考文献
[1]CRECRAFT D I.Ultrasonic measurement of stress[J].Ultrasonics,1968,6(2):117.
[2]陈毅.20CrMnMo齿轮齿根残余应力理论及试验研究[D].重庆:重庆大学,2013.
[3]冉启芳,费星如,邓朝栋,等.用超声波方法测量螺栓应力[J].固体力学学报,1982(1):64-70.
[4]杜刚民,李东风,曹树林,等.螺栓轴向应力超声测量技术[J].无损检测,2006(1):20-22.
[5]刘镇清,王路.一种以超声纵横波声时及温度为参量的螺栓轴向应力测量仪[J].仪器仪表学报,1996(6):662-665.
[6]江泽涛,朱士明.纵横波测已紧固螺栓轴向应力[J].应用声学,2000,19(1):16-21.
[7]江泽涛,张少钦,胡景春,等.微机化的纵横波螺栓轴向应力检测仪研制[J].固体力学学报,2001(4):415-420.
[8]张俊.基于声弹性原理的超声波螺栓紧固力测量技术研究[D].杭州:浙江大学,2005.
[9]贾雪,王雪梅,甘文成,等.声弹性效应螺栓轴向力标定试验研究[J].中國测试,2018,44(3):23-27.
[10]徐春广,李骁,潘勤学,等.螺栓拉应力超声无损检测方法[J].应用声学,2014,33(2):102-106.
[11]SUDA M,HASUO Y.Development of ultrasonic axial boltingforce inspection system for turbine bolts in thermal powerplants[J].JSME International Journal,1992,35(2):216-219.
[12]高辉.几类常用非线性回归分析中最优模型的构建与SAS智能化实现[D].北京:中国人民解放军军事医学科学院,2012.
[13]CHAKI S,CORNELOUP G,LILLAMAND I,et al.Combination of longitudinal and transverse ultrasonic wavesfor in situ control of the tightening of bolts[J].PhysicalReview C,2007,31(1):94-110.
(编辑:谭玉龙)\
