反比例函数期末复习

张珉

【重点知识点】

1.反比例函数的定义：一般地，形如y=kx（k是常数，k≠0）的函数，其中k叫做比例系数.

2.反比例函数的形式：y=kx;y=kx-1;xy=k.（k≠0）.

3.反比例函数的图像和性质：

①当k>0时，图像在第一、三象限内，且y随x的增大而减小（x、y的变化趋势相反）（图1）;当k<0时，图像在第二、四象限内，且y随x的增大而增大（x、y的变化趋势相同）（图2）.

②|k|越大，图像离原点越远.

WingdingsCB@

反比例函数具有轴对称性（对称轴为y=x和y=-x）和中心对称性（对称中心为原点）.

4.反比例函数中k的几何意义：反比例函数图像上的任意一点的横纵坐标之积等于比例系数k.

如图3.

S 矩形A 1P 1B 1O=S 矩形A 2P 2B 2O=S 矩形A 3P 3B 3O=|k|

如图4.

S △P 1A 1O=S △P 2A 2O=S △P 3A 3O=|k|2

如图5.

∵S △AOM=S △BON

∴S △AOB=S 四边形AONB-S △BON=S 四边形AONB-S △AOM

∴S △AOB=S 梯形ABNM

如图6.

①点A与C，点B与D分别关于原点对称，所以四边形ABCD为平行四边形，所以S 四边形ABCD=4S △AOB.

②当OA=OB时，四边形ABCD为矩形ABCD.

③∠AOB=90°，四边形ABCD不能成为菱形.

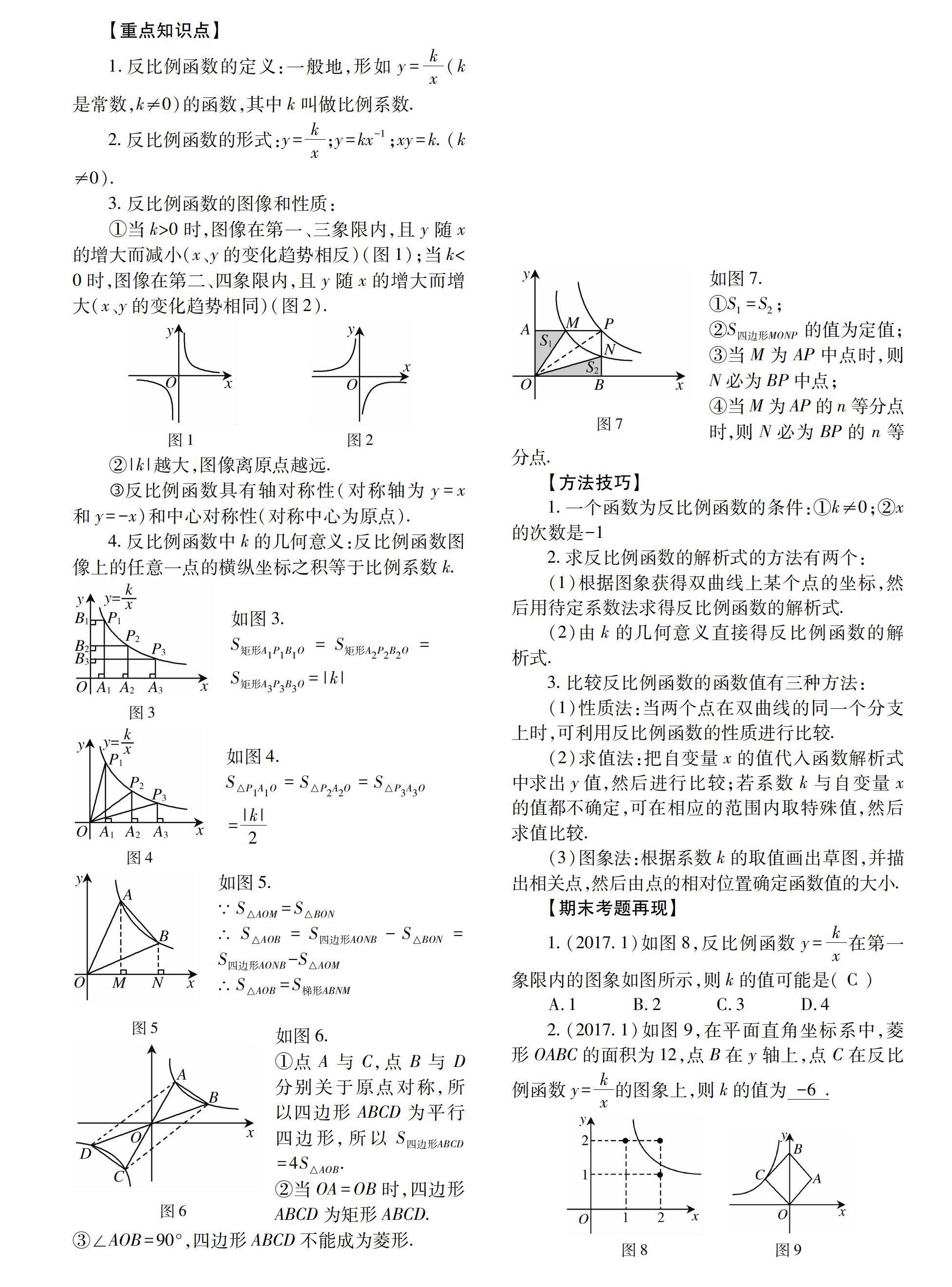
如图7.

①S 1=S 2;

②S 四边形MONP的值为定值;

③当M为AP中点时，则N必为BP中点;

④当M为AP的n等分点时，则N必为BP的n等分点.

【方法技巧】

1.一个函数为反比例函数的条件：①k≠0;②x的次数是-1

2.求反比例函数的解析式的方法有两个：

（1）根据图象获得双曲线上某个点的坐标，然后用待定系数法求得反比例函数的解析式.

（2）由k的几何意义直接得反比例函数的解析式.

3.比较反比例函数的函数值有三种方法：

（1）性质法：当两个点在双曲线的同一个分支上时，可利用反比例函数的性质进行比较.

（2）求值法：把自变量x的值代入函数解析式中求出y值，然后进行比较;若系数k与自变量x的值都不确定，可在相應的范围内取特殊值，然后求值比较.

（3）图象法：根据系数k的取值画出草图，并描出相关点，然后由点的相对位置确定函数值的大小.

【期末考题再现】

1.（2017.1）如图8，反比例函数y=kx在第一象限内的图象如图所示，则k的值可能是（ C ）

A.1B.2C.3D.4

2.（2017.1）如图9，在平面直角坐标系中，菱形OABC的面积为12，点B在y轴上，点C在反比例函数y=kx的图象上，则k的值为-6.