一类Wiener系统的动态环节的阶次辨识算法

祁国芳 景绍学 范梦松

摘  要：Wiener系统的结构特点，使得其线性动态环节的输出不可测量，导致现有方法无法直接用于Wiener非线性系统的线性环节的定阶。为了准确确定一类Wiener系统包含的FIR函数的阶次，提出了一种残差曲线斜率法。该方法基于残差曲线的斜率来获得FIR的阶次。并且，该方法在不进行参数辨识的基础上，仅利用测量到的输入输出输出数据，来获得FIR的阶次。该算法既减小了计算量，也提高了定阶准确度。数值仿真验证了算法的有效性。

关键词：Wiener系统;阶次辨识;残差分析

中图分类号：TP391.9     文献标识码：A

Abstract：Because the output of linear dynamic part is not measurable，the existing methods cannot be directly used to determine the order of linear part in a Wiener system.In order to determine the order of the FIR in a Wiener system accurately，a method based on the slope of the residual is proposed.This method obtains FIR order based on the slope of residual curve.This method only uses the measured input-output data to obtain the order of FIR，and need not estimate the parameters of the system.Thus，the proposed method not only reduces the computational burden，but also improves the accuracy of order determination.Numerical simulation validated the proposed algorithm.

Keywords：Wiener system;order identification;residual analysis

1   引言（Introduction）

近年来，非线性系统的辨识和控制引起了研究人员的广泛关注[1，2]。模块化非线性系统是一种结构化非线性系统，由线性动态模块和非线性静态模块组合而成。由于结构简单、实用性强，模块化非线性系统模型在非线性系统建模中获得了广泛应用，并引起了研究人员的广泛关注[3，4]。Wiener系统是一种典型的模块化非线性系统，由一个线性动态模块后面串联一个非线性静态模块组成的。目前，Wiener系统已经被广泛应用于工业系统的建模过程中。

现有的Wiener系统的辨识文献多集中于参数辨识领域：如文献[5]—文献[8]都是在系统结构已知的情况下对Wiener系统进行参数辨识，并且假设线性模块的结构形式和阶次、非线性静态函数的表达形式和阶次都是已知的。然而，在很多情况下系统的结构和阶次等先验信息并未被研究人员所掌握，导致辨识无法进行。另外，在模型结构已知的情况下，大多数传统算法都是先辨识含有参数乘积项的过参数系统，随后再进行参数的分离工作以得到待辨识的单个参数向量，算法的计算量很大，辨识代价很高，实时性较差。

基于上述难点，本文将研究一类Wiener系统的线性模块的阶次辨识问题。该系统的线性动态模块用阶次未知的有限脉冲响应函数（FIR）表示，非线性反函数为一个阶次已知的多项式函数。

2   问题描述（Problem description）

考虑如图1所示的离散非线性Wiener系统。图1中，和分别为系统的输入、输出信号。为线性动态子模块的传递函数，为非线性静态函数。为不可测中间变量。

5   结论（Conclusion）

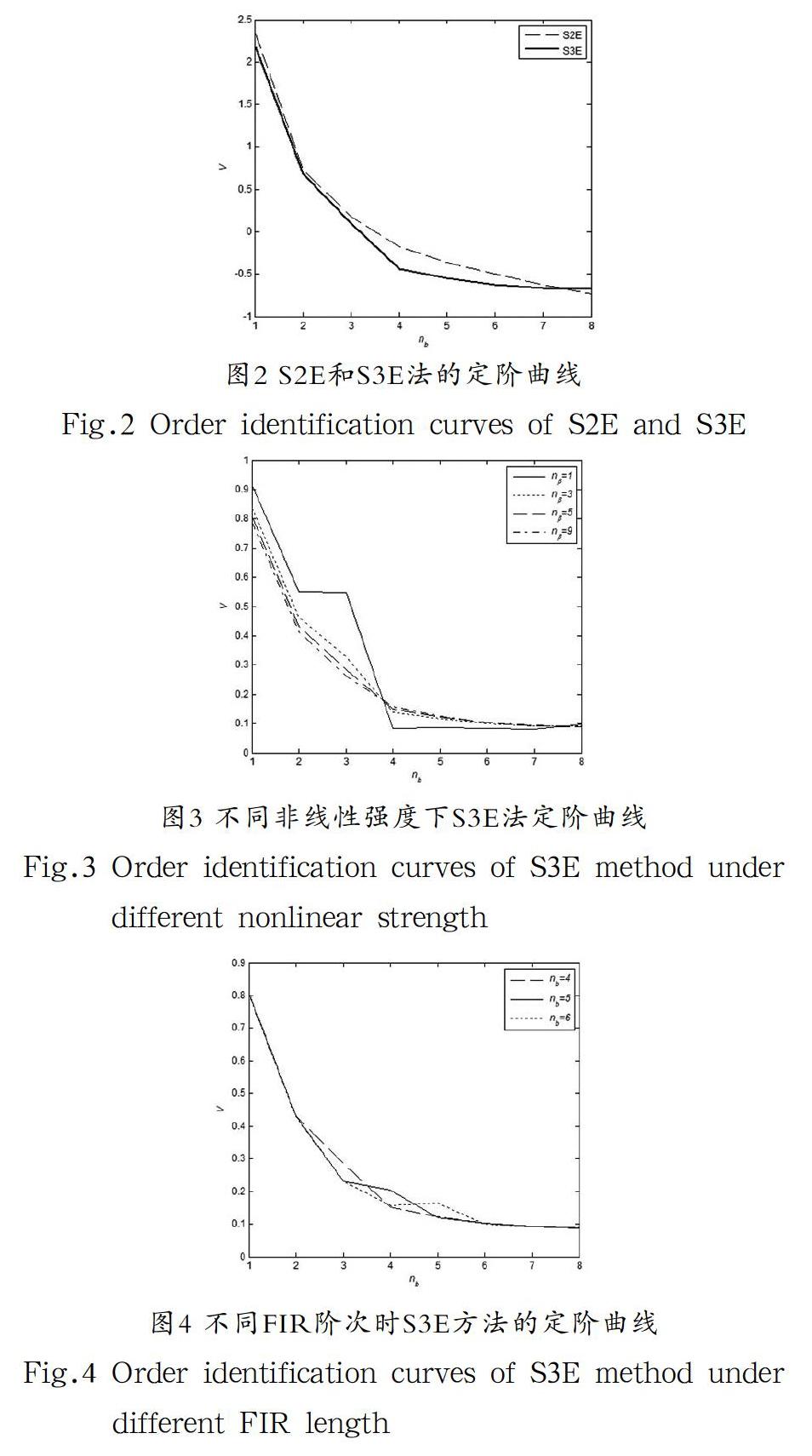
为了辨识一类Wiener系统的FIR函数的阶次，在传统残差方法的基础上，提出了一种残差曲线斜率法。该法首先直接利用系统的输入输出数据计算残差平方和，然后绘制残差曲线，再计算残差曲线斜率以用于FIR阶次的确定。数值仿真表明，所提的S3E定阶算法针对不同非线性强度和不同FIR阶次的Wiener系统，均能给出正确的FIR阶次估计。

参考文献（References）

[1] Jing S，Pan T，Li Z.Variable Knot-Based Spline Approximation Recursive Bayesian Algorithm for the Identification of Wiener Systems with Process Noise[J].Nonlinear Dynamics，2017，90（4）：2293-2303.

[2] Li J，Zheng W X，Gu J，et al.A Recursive Identification Algorithm for Wiener Nonlinear Systems with linear State-Space Subsystem[J].Circuits，Systems，and Signal Processing，2018，37（6）：2374-2393.

[3] Ahmed-Ali T，Tiels K，Schoukens M，et al.Sampled-Data Based State and Parameter Estimation for State-Affine Systems with Uncertain Output Equation[J].IFAC-PapersOnLine，2018，51（15）：491-496.

[4] 景紹学，李正明.Hammerstein-Wiener系统的递推贝叶斯参数辨识算法[J].计算机应用研究，2017（02）：105-107.

[5] 陈山，宋樱，房胜男，等.基于头脑风暴优化算法的Wiener模型参数辨识[J].控制与决策，2017，32（12）：2291-2295.

[6] Wang D，Ding F.Least squares based and gradient based iterative identification for Wiener nonlinear systems[J].Signal Processing，2011，91（5）：1182-1189.

[7] 景绍学，李正明.Wiener 系统的变聚点样条逼近递推贝叶斯算法[J].控制理论与应用，2017，34（1）：13-21.

[8] Li G，Wen C.Identification of wiener systems with clipped observations[J].IEEE Transactions on Signal Processing，2012，60（60）：3845-3852.

[9] 方崇智，萧德云.过程辨识[M].北京：清华大学出版社，1988.

作者简介：

祁国芳（1998-），男，本科生.研究领域：系统辨识.

景绍学（1976-），男，博士，副教授.研究领域：系统辨识，参数估计.本文通讯作者.

范梦松（1997-），女，本科生.研究领域：系统辨识.