高压电缆局部放电小波自适应阈值降噪方法

文/葛少伟 侯建峰 邝涛 王家斌 周金宝

1 引言

局部放电检测技术的难点之一是电力设备的运行环境复杂，并且局部放电属于瞬态微弱信号，局部放电监测设备常处于强电磁环境中，检测的原始信号一般包含多种干扰信号和不同类型的局部放电信号，不同类型的局部放电信号叠加同样也会给局部放电的诊断造成困难，因此要对局部放电进行准确测量前，必须对各种干扰信号进行排除，从而准确地进行电气设备故障诊断和故障处理。

本文提出了一种小波自适应阈值降噪方法，不但能够较好的保证信号的局部化特征，而且能够从复杂干扰中有效提取局部放电信号，可用于高压电缆局部放电降噪。

2 小波阈值降噪方法

用于局放信号的小波去噪方法主要有：模极大值法和阈值法两类。模极大值法实现过程比较复杂，重构信号误差较大。阈值法算法简捷，在局部放电信号去噪中应用较多。

一般来讲，小波阈值去噪主要由以下3个步骤组成：

（1）小波分解；

（2）小波分解系数阈值量化；

（3）信号重构。

2.1 小波分解

选定小波母函数和分解层数后，可以对信号进行多尺度小波分解。典型的3层分解见图1所示。

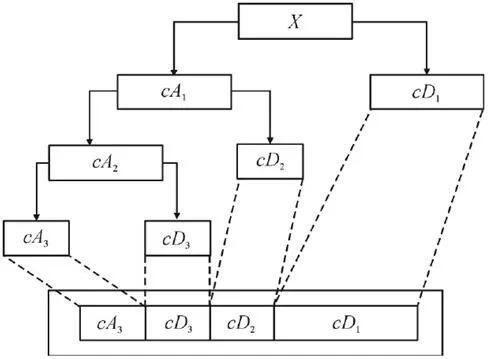
图1：3层小波分解结构

2.2 小波分解系数阈值量化

小波分解能够使有用的局放信号集中在小波域数值大的系数上，而噪声是分布在整个小波域上，对应的小波系数也较小，因此通过在不同尺度上选取恰当的阈值，将小于阈值部分的系数作为干扰噪声去除，从而实现降噪。阈值选取方法较多，主要有Sqtwolog通用阈值式、Heursure混合阈值式、Minmax最大最小准则阈值式等。

图2：局放信号与干扰信号模拟装置

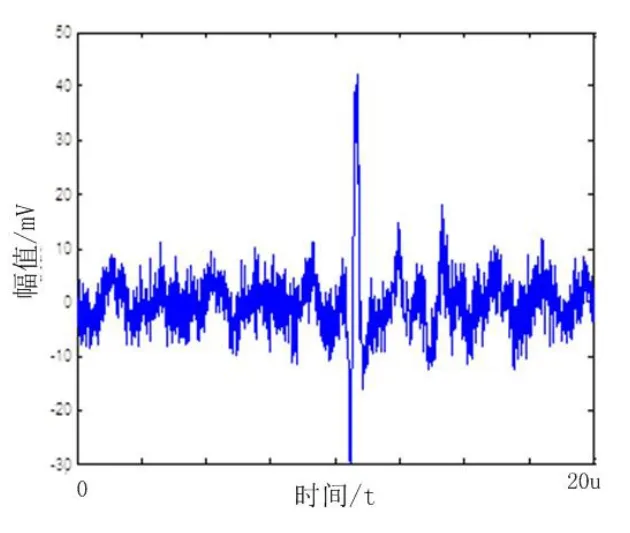
图3：原始波形

2.3 信号重构

根据小波分解底层得到的低频系数及阈值处理得到的各层高频系数，通过小波逆变换进行信号重构，最终实现去噪。

3 试验验证

为了验证局部放电中小波自适应降噪的效果，如图2所示，使用局放信号与干扰信号模拟装置在试验中将不同类型的局部放电信号与干扰信号相互叠加，对生成的数据进行小波降噪。

对图3中检测的原始信号波形经db4小波8层分解后分别选取：sqtwolog、regrsure、heursure和minimaxi四种阈值处理后的波形如图4所示。

从图4中可以看出，db4小波的8层分解对原波形的降噪效果比较理想，但是不同滤波阈值的选取对最终滤波后波形影响较大。从图4可以看出，minimaxi和sqtwolog阈值规则对高频脉冲的过滤效果最好，但是本试验注入的脉冲为单脉冲，滤波波形中实际的脉冲应为幅值最大的那个，然而在这两种阈值规则下，波形中的起始脉冲并不是实际注入的脉冲，即这两种阈值规则无法过滤实际脉冲前的一小段周期性的噪声信号。而在rigrsure和heursure阈值规则下，虽然这两种阈值规则对周期性噪声干扰的过滤效果一般，但是经过这两种规则的滤波后，波形中脉冲起始位置的信息仍被保留下来。在后续分析时使用的脉冲起始时刻判断算法中考虑到信号的噪声因素，需要对脉冲的噪声功率进行估计，因此不宜对原始信号进行过度的滤波处理。

综上因素，本章选择使用db4小波对检测点采集的信号进行8层分解，并用heursure阈值规则对分解后的高频系数进行滤波。

4 结论

本篇提出了一种小波自适应阈值降噪方法，不但能够较好的保证信号的局部化特征，而且能够从复杂干扰中有效提取局部放电信号，可用于高压电缆局部放电降噪。

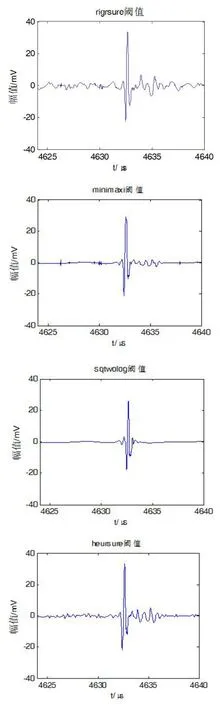
图4：滤波后波形