基于AHP-ADC模型的某型发烟车效能评估
2019-11-16蒋金利顾进李廷
文/蒋金利 顾进 李廷
科学技术日益发展,武器装备的性能逐步改善,并不断朝着复杂化、信息化、现代化发展。但是寿命短、效能低、效费比不高等一系列问题也随之凸显。实践证明,科学合理的进行武器装备效能评估对武器装备后续的再研发,作战试验的开展及配套保障体系的形成具有一定的指导意义。
本文研究了武器装备系统效能分析与评估的理论方法:首先介绍了 ADC评估模型,进而选择并综合分析了效能指标,进行了基于AHP-ADC的评估建模,然后选取某型发烟车,进行了实例分析。
1 ADC效能评估模型介绍
目前比较流行的有层次分析法(AHP),ADC效能评估模型,SEA分析法、模糊综合评判法等。本文提出一种基于AHP-ADC的效能评估方法,并结合常用的装备RMS参数进行计算,确保计算方法的可行性以及结果的真实性。
ADC效能评估模型是于20世纪60年代中期美国工业界武器武器系统效能咨询委员会(WSEIAC)提出的面向武器系统效能进行评估的方法。它的基本原理是基于可用度(A-Availability)、可信度(D-Dependability)和固有能力(C-Capacity)三大要素评价系统,将三大要素统一为标准的量度,给所装备一个数字化的评价。装备系统效能的表达式为:
E=A×D×C
其中:E-系统效能值,A-可用性向量,D-可信性矩阵,C-固有能力矩阵。
1.1 可用性向量A
可用度是在开始执行任务时系统状态的量度。
可用性向量A的一般表达式为:
该式中ai的含义是开始执行任务是武器装备系统处于i状态的概率,n表示的含义为系统可能出现的状态总量。
由此可见,n个可能出现的系统状态构成了武器装备系统的状态样本空间,显然
由于本文用此方法对于防化装备进行评估。根据防化装备的特殊性,其遭受敌方打击后一般不再具有作业能力,故本文中将可用性状态进行简化,分为可用与不可用两种。将可用状态记为1,不可用状态记为2,则

式中a1为开始执行任务时武器装备的可用度;
a2为开始执行任务时武器装备的不可用度。
根据装备保障工作中的可靠性理论可知:

表1:RMS权重专家打分表

表2:可靠性指标权重打分表

表3:故障性指标权重打分表

表4:保障性指标权重打分表
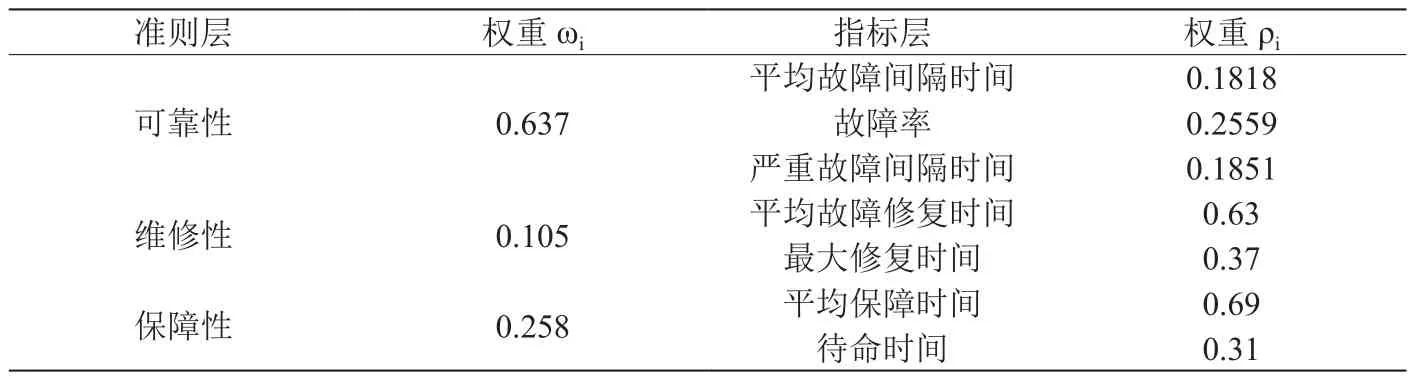
表5:综合权重表
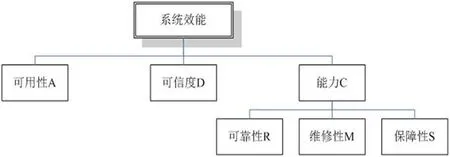
图1:效能评估结构图
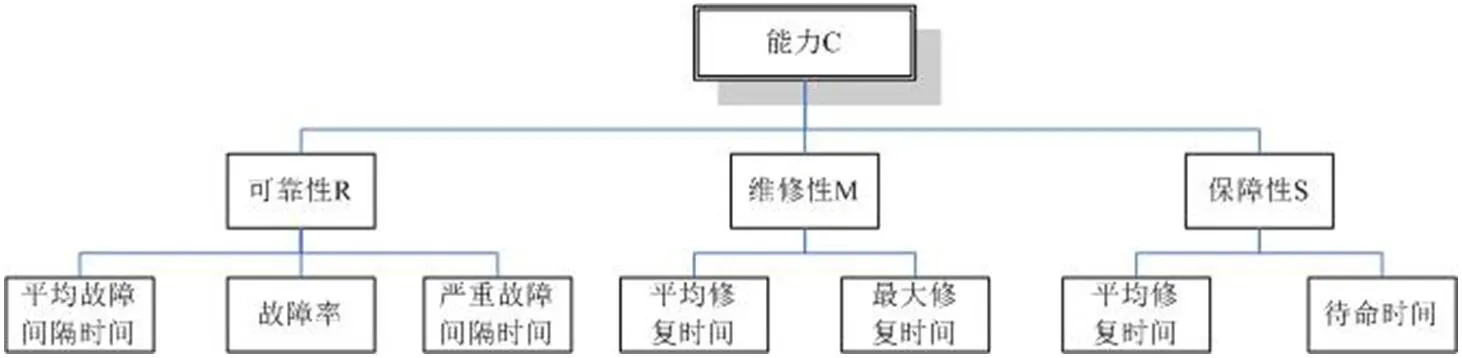
图2:能力C的指标划分图

式中MTBF-平均故障间隔时间;MTTR-平均故障修复时间。
1.2 可信度矩阵D
可信度是指已知当前的工作状态,在任务过程中某个时刻状态的度量。其表达式为:
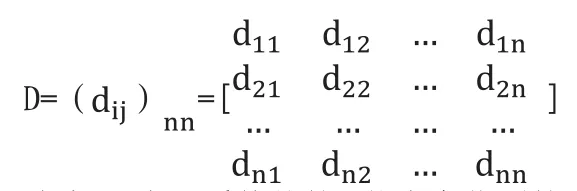
式中dij表示系统从第i状态变化到第j状态的概率。
如果系统在运行期间不可修复,且不能带故障工作,则系统可信度指标就是可信度;如果运行期间系统可以修复,则当系统有n个故障状态时,可信度指标是n阶方阵式,而可信度指标是可信度方阵的对角元素。
评估系统的可信度首先是要明确系统故障,确定系统运行和维护条件,并且仔细考虑每个任务剖面的部件数,故障情况,最后,综合各组合和全系统的可信度。
1.3 能力C
C是指在系统执行任务的当前状态下,武器装备完成规定任务的度量。显然,能力C与系统状态有很大关系。
C是ADC效能评估模型中最重要的因素,也是最难确定的因素。一般情况下,这一因素与武器装备系统中的多个指标相关,不同的指标,权重不同,影响方式也不同,在C中所发挥的作用也有很大差异。为了同一这些指标的量纲,引入效能值的概念,效能值是一个实数,其大小应属于区间[0,1]。
如果直接将C带入效能评估方程中去计算系统的效能,那么,对于单项效能评估来说,C就是一个向量:

对于评估多项效能来说,C就是一个矩阵:
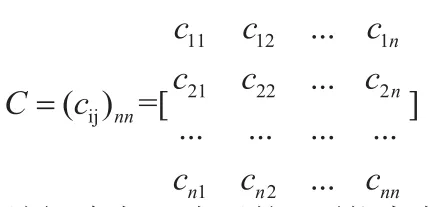
该矩阵中cij表示第j项能力在状态i下完成任务的度量。
2 基于ADC与AHP的效能评估方法应用
针对ADC效能评估模型中能力向量C不容易确定的问题,本文中提出用层次分析法来确定能力向量C。
为了使判断分析定量化,形成判断矩阵,引入了9标度法。
效能评估结构图如图1所示。
2.1 确立以RMS为基础的指标体系
可靠性、维修性、保障性(简称为R&M&S)是衡量武器装备质量的重要特性,它在设计讨论和生产制造过程中形成,在使用阶段得以体现,贯穿于武器系统全寿命管理的过程中,是当今武器装备论证、设计时必须重点关注的特性。
防化装备是军队装备的重要组成部分,是核化生防护的物质基础,在未来作战和装备建设中处于不可或缺的重要地位。对防化装备R&M&S进行研究,为提高防化装备的质量效能提供理论指导,对提高防化装备的作战保障能力,充分利用维修资源和降低保障费用等都将产生直接的影响。
所以,对其进行效能评估,以RMS指标为基础。先由AHP方法确定C的效能值,将指标分为比较成熟的影响装备效能的RMS参数,进行以可靠性,维修性和保障性为指标基础的层次分析,得出权重向量。最后再由ADC评估模型,得出最终效能。
在RMS的基础上,将RMS的指标再次细分,如图2所示。
2.2 AHP-ADC方法建模
2.2.1 可用性向量A的计算
对于某型发烟车来说,前文已经假定只有可用与故障两种状态,可用MTBF和MTTR来计算:
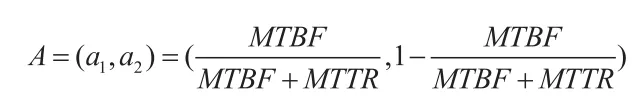
2.2.2 可信度矩阵D的计算
一般来说,某型发烟车只有可用与故障两种状态,故可信度矩阵为:
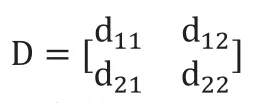
一般情况下,装备出现故障概率的时间服从指数分布,则:
d11=e-λt,d12=1-e-λt
其中:λ 为系统故障系数,t为一次执行任务的时间,为简单起见,本文假定任务过程中遭受故障不可修复,故障状态无法向完好状态转变。所以,d21=0,d22=1。则可信度矩阵为:
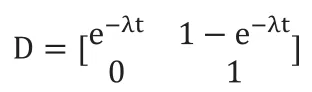
2.2.3 能力向量C的计算
能力向量C采用AHP流程进行计算,由于系统状态前文假定只有两种。并且故障状态下,没有完成任务的可能性,故能力向量C为:
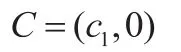
(1)用层次分析法确定权重向量。
设准则层权重向量为

应用 1-9的比例标度方法对同层因素进行两两比较量化,形成判断矩阵。由于矩阵是由Delphi法得到的,所以必须进行一致性检验。
(2)求出能力C。
其中,ωi为相对权重,ρi为效能值。
3 某型发烟车效能评估实例
本节对某型发烟车进行效能评估,验证模型的可行性与准确性。
进行评估时,可用性 A和可信度 D采用客观计算,能力 C则采用 AHP 方法。并且,在天气条件良好的外界环境进行试验,尽量能发挥某型发烟车的真实效能。
(1)某型发烟车发烟系统为串联系统,任一部件发生故障,则整体故障,故系统的MTBF应该由部件的最小MTBF决定。一般情况下整个系统的平均故障时间大于1000 小时,基层级修复时间小于1小时,故
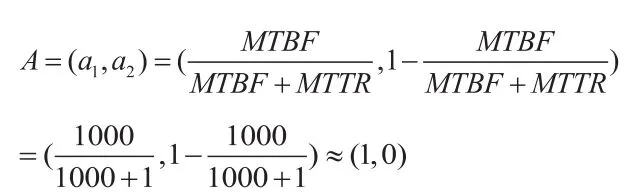
(2)由于某型发烟车的平均故障时间为1000 小时,则平均故障率为:

执行任务的时间这里为装备展开时间,启动时间,烟幕形成时间,连续发烟时间和装备撤收时间的总和,即:
t=3+3+3+30+3=42分钟=0.7小时
那么,可用度矩阵D 为:
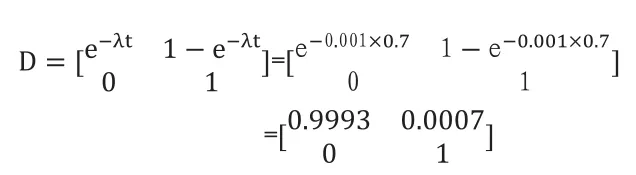
(3)首先Delphi法得到指标权重表,并将其按照指标结构分别评判准则层和指标层,再基于AHP得出判断矩阵。如表1所示。
由此,可以得出准则层对目标层的判断矩阵为

同理,得到专家打分表2,3,4,并得出相应判断矩阵。
故,可得判断矩阵

故,可得判断矩阵

故,可得判断矩阵
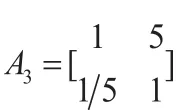
(4)计算权重。
由所得矩阵,根据和法求出λmax和特征向量,并进行一致性检验。
对于矩阵G:λmax=3.04,对应特征向量为:
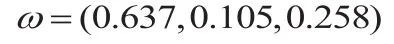
进行一致性检验,C.I=0.02<0.1,经修正后,C.R=0.034<0.1,一致性良好。
对于矩阵A1:λmax=3.09,对应特征向量为:
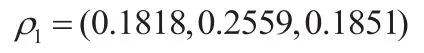
进行一致性检验,C.I=0.045<0.1,经修正后,C.R=0.077<0.1,一致性良好。
对于矩阵A2:为λmax=2.03,对应特征向量为:
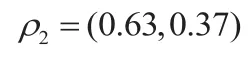
进行一致性检验,C.I=0.015<0.1,二阶无需修正,一致性良好。
对于矩阵A3:为λmax=2.08,对应特征向量为:

进行一致性检验,C.I=0.04<0.1,二阶无需修正,一致性良好。
(5)计算能力向量C。
根据步骤(4),可得综合权重表(表5):

(6)计算综合效能
根据ADC评估模型,系统的效能E的计算公式为:

4 结论与不足
本文设计了以RMS性能指标为基础的基于AHP-ADC方法的效能评估模型,并应用该模型对某型发烟车进行了效能评估,并计算得到了最终的效能值。通过对模型的应用,证明该方法可行。
虽然模型可行,但仍存在一些不足之处。
(1)对于RMS指标权重的选取客观性不够。
(2)战场环境因素更加复杂多变,武器装备效能不止两种状态。
(3)如何更好的解析能力向量C,还有待进一步加强。
