基于计算机模拟的救助中心问题
2019-11-16周思忆肖晰翟宏强
文/周思忆 肖晰 翟宏强
1 问题的重述
1.1 背景知识
1.1.1 背景介绍
城市生活的大型中心设施通常管理着多个移动服务点,当城市某地点产生需求的时候,将从中心设施派出移动服务点赶往需求地点进行服务。需求是否以最快的速度得到响应,与诸多因素有关。例如,从中心设施赶往现场所要的时间、接受服务的时间、等待的时间等。在服务力量有限情况下,如何根据以往需求产生的情况、道路状况,将中心设施建在合适的位置显得尤为重要。
1.1.2 提出问题
根据城市地理简图以及各地区呼叫救助队的时刻,通过改变紧急医疗中心设施位置,降低平均响应时间,求出其最小值,以及此时中心设施所处位置。
2 模型的假设
(1)假设救助中心到每个救助区域的所有路径道路状况相同,不能存在堵车。
(2)假设各救援队的行驶速度为1km/min。
3 名词解释与符号说明
3.1 名词解释
平均响应时间:从一个呼叫产生到救助队赶到该呼叫地点所用的平均时长。
3.2 符号说明
如表1所示。

表1

图1:区域图网络
4 模型的建立与求解
4.1 问题的分析与求解
4.1.1 对问题的分析
经分析,平均响应时间与救助队到救助区域的距离有关,因为为了能尽快到达救助地,必须求得救助中心到各救助区域的最短距离。因此首先根据迪杰斯特拉算法建立最短救助路径模型,得到救助中心到达救援区域的最短距离。再分析,发现呼叫地点、呼叫时间间隔不服从常见的均匀分布、正态分布、泊松分布、指数分布,故呼叫地点、呼叫时间间隔为一般分布,故用累积分布列的方式表诉它们的分布规律;并假设救援时间服从均值为15、方差为1的正态分布。最后在前两步的基础上,建立基于计算机模拟的平均响应时间模型,求得平均响应时间。
模型Ⅰ——基于计算机模拟的平均时间响应模型:
4.1.2 模型的准备
4.1.2.1 确定救助中心到各区域距离
(1)分析。紧急医疗中心派出的车辆到救助地点之间的路径不是唯一,如果时间稍微延误,将造成不可挽回的损失。因此,车辆必然会选择到救助地的最短路径,如何求解从紧急医疗中心到救助地点的最短路径成了解决问题一的前提。本文使用迪杰斯特拉(Dijkstra)算法计算一个节点到其他节点的最短路径。
(2)分步求解。
步骤一:确定救援位置。
如图1所示,45个救助区域分别占据的面积是一块小矩形。矩形边为公路,每条边均长1.5公里。救援时,无法得知具体救助位置处于小矩形区域哪一块。为方便计算,把45个区域的位置看成一个一个的节点,将节点之间的连接关系转化为图论里面的“图”。故建立“图”网络。
步骤二:建立图网络。
如图1所示,其中的一个小圆代表一个区域节点,小圆中的数字代表区域号。节点与节点之间的公路用一条线段表示,连接节点与节点之间的每条线段均为1.5公里。
步骤三:确定算法思路-迪杰斯特拉算法。
a.指定一个节点,计算该点到其他点的最短路径。
b.引入两个集合(S、U),S集合包含已求出的最短路径的点(以及相应的最短长度),U集合包含未求出最短路径的点(以及A到该点的路径及长度,若两点间没有连通,则距离记为无穷)。
c.初始化两个集合,S集合初始时 只有当前的源节点以及路径长度0。
d.从U集合中找出路径最短的点,加入S集合。
e.若源点到步骤d加入集合S的点的距离加上该点到集合U中某点的距离小于源点到集合U中某点的距离,则更新U集合路径,更新为前者。
f.循环进行d、e步骤,直至集合U中所有节点都加入集合S。
步骤四:基于迪杰斯特拉算法建立最短救助路径模型。
a、创建一个距离的矩阵W,Wij表示第i个节点到第j个节点(距离)。
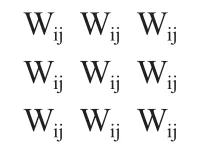
b、本题救助中心在节点16,故建立第16个节点到其他节点的距离矩阵W,初始化为无穷。
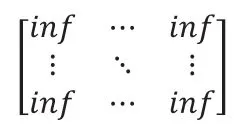
c、录入节点之间的距离,如区域2到区域3的距离为1.5公里,则W23为1.5。
d、visited用于记录节点是否已经放入集合S。
e、建立目标变量,即最短路径长度,用shortPath记录。
步骤五:最短救助路径求解
将12个区域分别作为救援中心距离其他地区的分别求解结果。
步骤六:最短救助路径结果分析。
由上述可知,将每个区域都看成一个一个的节点,各区域到其他区域的最短距离是为了求解本题平均响应时间所做的提前准备。
4.1.2.2 确定分布
(1)呼叫地点的分布。对8天的呼叫地点进行统计,用matlab画出频数分布直方图。得到呼叫地点和均匀分布、正态分布、指数分布、泊松分布的符合情况,然后使用spss软件对这些数据进行Kolmogorov-Smirnov检验。从图中找出数据四种分布的渐进显著性水平,若大于0.05,为对应分布,否则不服从这四种分布,认为它服从一般分布。本题四种分布的渐进显著性水平为0,呼地点服从一般分布。
(2)呼叫时间间隔的分布。将呼叫地点转换成的频数分布直方图,用同样方法确定呼叫时间间隔属于一般分布。
(3)救援时间的分布。已知一次救援的时间服从均值为15,方差为1的分布,假设它服从均值为15,方差为1的正态分布:

其中μ=15,σ=1。
根据[0,1]区间上服从均匀分布的随机数确定随机变量的值:
如每次呼叫时间间隔、呼叫地点、每次的救援时这些随机变量的分布为:
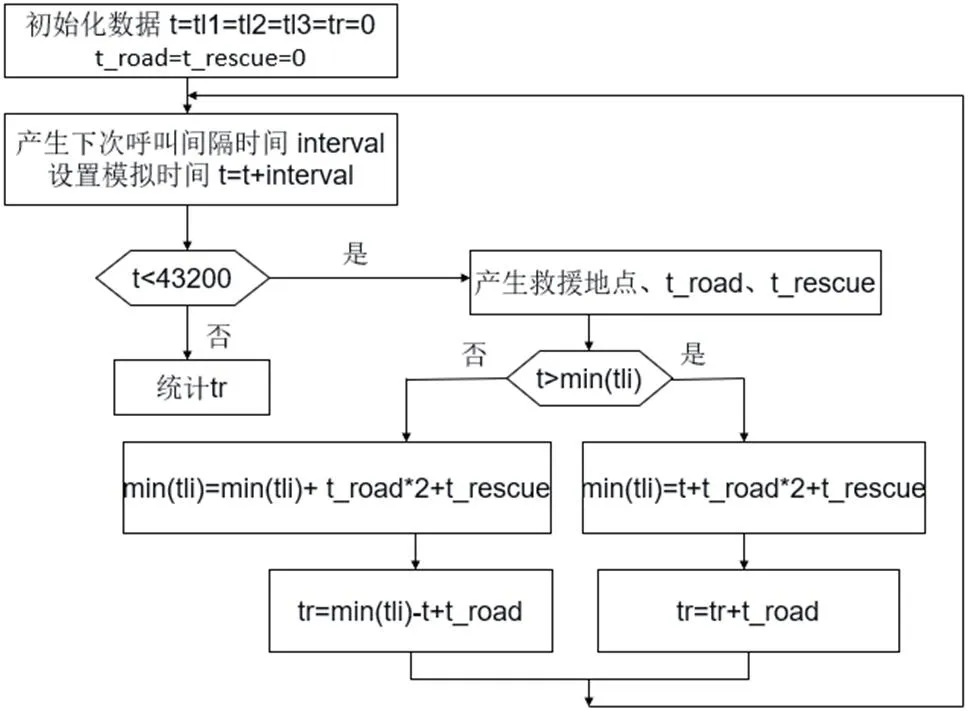
P{X=xi}=pi,i=0,1… 其中0 将概率分布转化为累计分布,令: 对于[0,1]区间上服从均匀分布的随机数ζ,取满足 式子的xi为本次随机变量的值。 4.2.1 模型说明 图2:计算机模拟流程图 通过计算机模拟程序,生成每次呼叫时间间隔以及地点的分布规律,生成每次呼叫产生的时间间隔和相应的地点,按照某种确定的派出救援队的算法对一天或若干天救助队的救助情况进行模拟,最后通过模拟,可以算出救助中心在不同地点的时候所对应的平均响应时间。t为当前时刻,tl1为第一个救援队返回的时刻,tl2为第二个救援队返回的时刻,tl3为第三个救援队返回的时刻,interval为下次呼叫的间隔时间,tr为总的响应时间、t_road为救援中心到救助点单程时间、t_rescue为本次救援所用时间。 具体模拟过程如图2所示。 模型——基于计算机模拟的最优救助中心选择模型: 4.2.2 模型的建立 (1)模型说明。 先求出各区域的平均响应时间,找出使平均响应时间最短的区域即要选择的救助中心。将第n次模拟的总平均响应时间控制到最小,作为约束条件,加上min trn。在此条件下求得目标变量,则中心区域为第j个区域pj。 (2)建立模型。 4.2.3 模型的求解 求解结果: 问题求解结果为:将救助中心设置在区域36,此时最短平均响应时间为18.6238分钟。
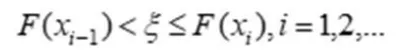
4.2 模型的建立