随机系统中粒子滤波算法

文/周英 李凯 周宇媚

1 引言

滤波是系统的状态估计问题。经典的卡尔滤波算法提供了线性高斯问题的最优解决方法。然而现实生活中存在大量非线性特性的实际问题。粒子滤波算法在非线性、非高斯系统中表现出噪声模型和系统模型不受限制，精度高等优点。因此，它的应用十分广泛，如：目标跟踪、目标定位及导航、通信领域、军事领域等。

标准粒子滤波算法中，退化现象无法避免。经过若干次迭代，少数有效粒子占据粒子集的大部分权值，而大部分粒子的权值很小。随着迭代的继续进行，甚至会出现一个或几个粒子权值非常大，而其他粒子权值基本为零的情况，这就是粒子集的退化分布。若迭代次数越多，大量的计算资源就会消耗在处理那些微不足道的粒子上。

2 粒子滤波及其仿真

粒子滤波以贝叶斯推理和重要性采样为基本框架。它源于蒙特卡罗思想，即以某事件出现的频率来指代该事件的概率。在滤波过程中，需要用到概率的地方，我们只需对变量进行采样，以大量采样及其相应的权值来近似表示该概率。基于此，粒子滤波算法可以在滤波过程中处理任意形式的概率。这也正是粒子滤波的一大优势。

粒子滤波过程分为初始状态阶段、预测阶段、校正阶段、重采样阶段、滤波阶段，由此循环往复。粒子滤波算法与卡尔曼滤波算法类似，需要知道系统的模型。如果系统模型未知，必须构建一个模型来进行模拟。通常构建模型是通过数学表达式来进行，其中包括系统状态方程和测量方程。

本文中采用一个应用广泛的标量模型对粒子滤波算法应用进行仿真分析。假定在任意状态下，系统的数学方程式如下：

状态方程：

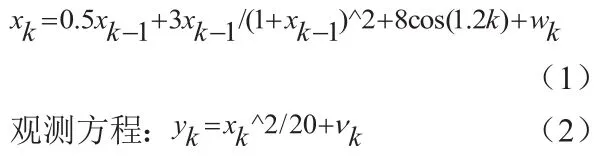
在公式（1）中，xk表示系统在k时刻状态值，xk-1表示系统在k-1时刻状态值，wk表示过程噪声，xk和xk-1是非线性关系。

在公式（2）中，yk表示系统在k时刻的测量值，vk表示测量噪声，yk和xk也是非线性关系。

当k=0时，表示系统处于初始状态。由于系统开始对x(0)一无所知，所有我们认为x(0)在全状态空间内平均分布。然后将所有采样输入状态转移方程，得到预测粒子。仿真过程基于（1）和（2）式，采用SIR粒子滤波算法，每次迭代都用系统重采样机制，得出仿真图如图1、图2。

从图1可以看出测量噪声值V、过程噪声值W、状态值X、观测值Y的变化情况；从图2可以看出，系统在wk、vk均值为0；Qk=10，过程噪声方差，Rk=1，测量噪声方差的噪声情况下，得出滤波器估计值和系统真实值。该滤波器估计输出采用了最大后验概率和后验均值两种方式，这两种方式均能反应出滤波估计的状态能很好地跟随真实状态。

3 粒子滤波算法的改进及仿真分析

上述基本粒子滤波算法中，因为Q和R的值获取比较困难，同时考虑到粒子退化现象等问题，做出改进。改进的方法有如下几种：

（1）增加粒子数；

（2）提高重采样技术；

（3）选择合适的建议密度。

本文从选择合适的建议密度方法着手，改进粒子滤波算法。因在产生建议分布方法中，局部线性化是一种较好的方法。UKF（无迹卡尔曼滤波）就是局部线性化方法的一种，它要求系统是近似的高斯后验分布模型，是一种递归的最小均方误差估计方法。将UKF方法引入到粒子滤波算法中，就是本文改进策略。

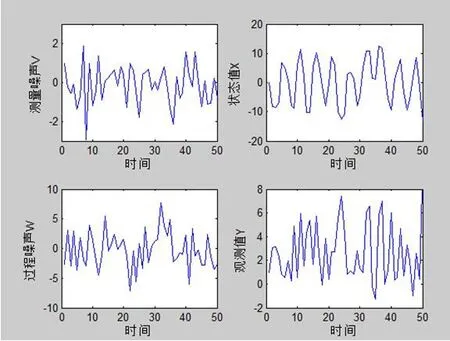
图1：各参数值变化情况

图2：非线性条件下粒子滤波仿真图

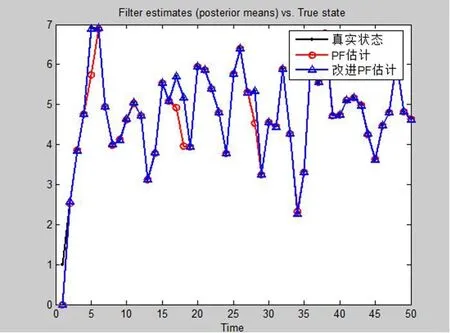
图3：系统状态图

该算法非常重要的环节就是：在采样期间，用UKF算法给每个粒子计算其均值和方差，然后“指导”系统的采样。也就是在粒子滤波算法的框架下，采用UKF算法得到最新的观测信息，给每个粒子产生合理的高斯建议密度分布。其算法流程如下：

（1）初始化；

（2）重要性采样；

（3）重采样；

（4）输出。

现在选用一维系统来仿真基本粒子滤波和改进粒子滤波算法。假定在任意状态下，系统的数学方程式如下：

从图3的仿真结果得出，PF(基本粒子滤波)算法和改进的PF算法都较好地跟随了系统的真实值；从图4的仿真结果可以看出，改进的PF算法偏差能在较短时间内达到极低水平，后续基本维持该水平，而PF算法的偏差值存在不小的波动；从图5的仿真结果看出改进的PF算法所耗去的计算时间较PF算法长，因此实时性较差。

4 结论

本文从改善建议密度分布角度改进粒子滤波算法，在跟随真实系统的可靠性方面得到改善，但其计算量较大，响应速度不快，同时系统还局限于高斯模型。因此，PF算法的改进还可与其他算法进行组合，如神经网络等结合改进，使其不受线性高斯模型限制，性能更强。

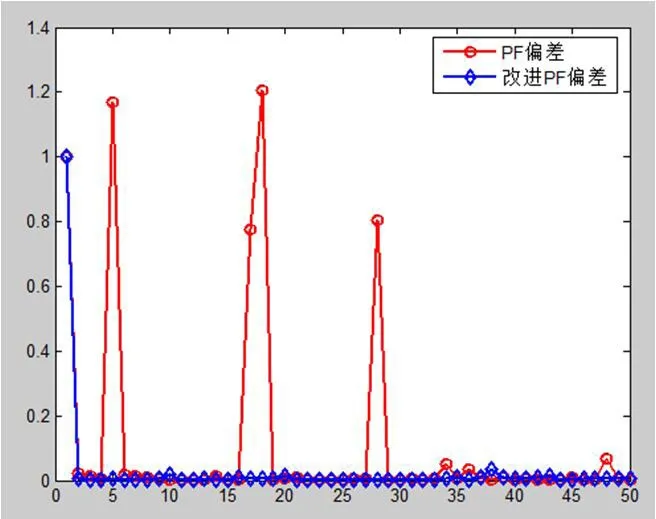
图4：系统状态偏差图

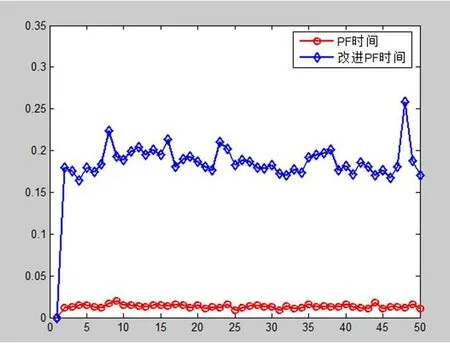
图5：系统实时性比较