基于边缘信息图像条件的盲去模糊算法

文/孙艳娜 吴海游

图像盲去模糊问题属于图像处理以及计算机视觉领域中的经典研究问题，它的技术应用内容丰富且技术应用难度较大，专门针对实际模糊图像的退化相关内容进行研究，并可实现相对复杂的技术应用。不过当前由于国内外针对该技术的研究还依然处于理论研究与仿真研究阶段，所以在实践操作中对图像模糊处理的应用效果依然还表现并不到位，所以基于多点要素展开对图像盲去模糊算法的研究还是非常有必要的。

1 图像盲去问题的不适定性研究

图像盲去问题中是存在不适定性的，它可以被理解为不失一般新，结合给定退化模型对图像去模糊内容进行分析，主要讲就是根据模糊图像g求解清晰图像u，基于这一点需要从数学意义层面上解读相关内容，即将其图像退化视为是一种正交换过程，并深度研究图像盲去模糊问题背景下的逆变换稳定性问题、存在性问题与唯一性问题等等。而在该过程中，还必须解释微小误差与少量噪声问题，因为它们会导致图像出现大幅偏差，必须加以修正。可考虑从数值分析角度分析由病态造成的图像去模糊问题不适定性问题，并构建退化模型，利用最小二乘法对图像去模糊过程进行计算，如下：

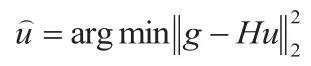
首先需要假设模糊核矩阵H中的已知条件，利用图像去模糊问题转化求解欧拉—拉格朗日方程得到：

如果矩阵HTH出现非奇异情况，则它的大小应该为M×M非负定矩阵，通过矩阵H可计算出M个非负定矩阵。这里必须考虑到矩阵H可能存在的高度病态，它的较小奇异值应该无限接近于0，且它所对应的奇异向量也会存在一定的高度震荡性，此时需要对它的H、g值进行计算，计算其非稳定性变化。

总体来说，正因为图像盲去模糊问题中所存在的不适定性要素，导致它其中的模糊核信息未知，应该基于问题的解释空间与非盲去模糊问题进行分析，看二者哪一点表现更突出明显，并着力对它的病态性表现内容进行分析，为此需要思考如何减弱其奇异值，基于基本思想配合对问题结构内容与附加约束条件进行验证，将其中可能存在的不适定问题转化为适定问题，以便于更好基于边缘信息图像条件运用盲去模糊算法，优化算法应用过程。

2 基于梯度稀疏性的图像非盲去模糊算法应用

为了解决存在于非盲去模糊算法中的不适定性问题，提高图像提取质量，应该考虑基于梯度稀疏性的图像非盲区模糊算法循序渐进复原图像，具体来讲图像的复原方法包括两点：估计模糊核以及估计清晰图像，基本流程应该先估计模糊了，然后再利用非盲去模糊算法恢复获得清晰图像，所以可将其视为是专门用于解决不适定问题的反问题类型。在具体的运算过程中应该首先引入一定的先验技术内容，结合约束未知图像对降低空间位置图像，计算图像自由度，或者基于变换域稀疏性先验对非盲去模糊算法内容进行计算调整，最后对模糊结果进行分析，进一步提高图像去模糊效果。基于此，本文提出了一种基于梯度稀疏性的二阶段图像非盲去模糊算法。

2.1 二阶段图像非盲去模糊算法流程分析

在首个阶段，要结合图像变换域中的稀疏性基础展开针对性计算分析，利用标准梯度作为分析算子基础，强调对稀疏性描述内容的有效增强，同时引入范数可作为增强稀疏性描述的一种方法，如此可有效恢复出图像中的边缘结构。在该基础之上，还需要进一步提升图像的去模糊质量；再进入下一阶段引入图像的非局部相似性作为是先验信息，提出边缘结构相似性约束项，确保算法在第一阶段就能恢复出锐利边缘。而针对两阶段还要建立图像非盲去模糊模型，采用数值算法求解，获得仿真实验结果，最终即可提出模型算法，复原清晰图像，同时还能保证图像细节把握到位，从而实现对Gibbs效应图像边界位置的科学合理抑制。

2.2 图像的非局部结构相似性研究分析

要在研究中提出梯度稀疏性回归模型，要结合两阶段图像的非盲去模糊算法对图像进行非局部结构相似性的分析，实现图像全局的滤波处理，满足去噪均值处理条件。基于实验结果分析图像非局部中可能存在的冗余性特征内容，始终确保图像的边缘结构与噪声能够得到合理抑制。去噪算法的关键在于建立盲去模糊算法的稀疏矩阵，基于实际计算相关非局部模型模块内容，由此可推导出基于梯度稀疏性的图像非盲去模糊模型算法。

2.3 基于梯度稀疏性的非盲去模糊模型算法应用研究

基于梯度稀疏性的非盲去模糊模型算法应该结合两个阶段展开：首先第一阶段尝试恢复图像中的显著边缘，它的显著边缘是模糊的，且存在大面积的纹理结构内容，需要构建回归模型基本约束，并对复原图像质量进行提升优化调整。下文主要结合这两个阶段进行深入分析：

首先在第一阶段，主要是基于梯度稀疏性进行图像非盲去模糊计算。利用现有的一类经典图像去模糊算法，可对图像中的非盲去模糊问题进行建模，并给出稀疏性正则化优化问题，最终求解获得结果，如下：

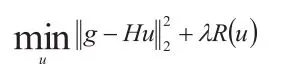
在该算式中，有R(u)表示稀疏正则化函数，λ表示正则化参数，二者具有不适定性属性，可以进一步将R(u)转换为如下形式：

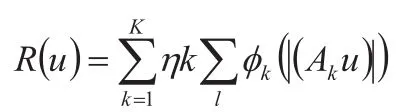
这其中的Ak表示第k个变换分析算子，主要结合Aku中的不同元素进行分析，基于多尺度几何分析理论分析算子Ak中的多种选择，如此可有效恢复所提取图像中的显著边缘结构模糊部分。在该过程中，还要尝试选取相应的图像非盲去模糊模型也会最终转化为带有耦合梯度算子的有约束优化模型（从无约束优化模型转换），并提出相应的拉格朗日函数。在该阶段可假设模糊矩阵H空间不变，可基于周期边界条件建立块循环卷积矩阵，再采用FFT进行快速求解。

在进入第二阶段后，要基于非局部自回归模型图像质量提升进行计算。采用梯度稀疏性作为先验约束，确保图像显著边缘与大尺度纹理结构能够明晰化，结合细节部分进行二次恢复，提升其图像质量。在该过程中，需要基于非局部自相似正则化约束项进行具体分析，建立NxN大小的单位矩阵，并通过自回归权值矩阵计算相关内容。另一方面，要保持图像中边缘结构，提出新绝缘结构相似性约束项，获域内像素的平均灰度值，基于边缘结构相似性约束项进行再次计算，获得非局部自相似性与边缘结构相似的图像模型，并实现模型优化调整。在解决优化问题过程中，需要建立3个二次目标函数，其中设置两个正则项，并对数据保真项进行分析。虽然在直观感受上其形象较为复杂，但通过适当改写可给出等价形式转化，基于梯度下降法求得全局最优解。最后通过最优解就可获得两阶段的图像非盲区模糊算法。

2.4 基于梯度稀疏性的非盲去模糊模型算法应用结果分析

基于梯度稀疏性的非盲去模糊新算法应用结果明显，主要是对于图像质量的提升效果良好，这也说明了该算法的应用有效性。首先从视觉上应该直观感受各种算法的去模糊效果。例如可选择一个图像算法尝试进行计算，选取一个大小为28x28的运动模糊核，利用清晰图像卷积算法计算获取仿真模糊图像。如果从视觉效果上看，目的是为了较好抑制图像边界位置的Gibbs效应，保证图像细节设计到位。

而在进入第二阶段后需要对图像质量进行进一步的提升调整，利用图像细节内容对图像质量效果进行改善，并在改善后验证存在于模型中的非局部结构内容，优化其结构相似性问题，实现对图像内容的有效计算，恢复图像的边缘结构部分，并结合客观指标评价两种对比算法，获得最终计算结果。

3 总结

总而言之，基于图像盲去模糊问题实现图像复原是当前非常热点的研究课题，它为天文观测、遥感成像、公共安全等领域提供了必要的技术支持，提高了这些领域中的图像提取效果，并结合图像盲去模糊中的模糊核估计算法对图像显著边缘结构进行了有效提取，并设计了相应的模糊核盲估计模型算法和梯度域下的稀疏性内容，进而在两阶段的原酸中有效抑制了存在于图像边界的Gibbs效应在图像视觉观感效果方面取得了良好效果。