基于移动质量-频率曲线的结构损伤识别方法

张青霞

摘要：针对土木工程中结构实测得到的模态信息少，结构损伤识别方法对噪声敏感且依赖高精确度有限元模型等问题，提出利用移动质量-频率曲线识别结构损伤的方法。首先，在结构上附加移动质量块，获得结构频率关于附加质量位置的关系曲线;然后，建立结构近似有限元模型，通过计算实际模型与近似有限元模型之间的质量-频率曲线的相关性，建立目标函数进行优化;最后，利用变截面简支梁结构进行数值模拟。结果表明：在模型存在较大误差情况下，该方法仍能够准确识别损伤位置，验证其具有较高的适用性。

关键词：结构健康监测;损伤识别;目标函数;频率

中图分类号：TU318

文献标志码：A

文章编号：1674–5124（2019）03–0001–06

Structure damage identification based on the curve of moveing mass and frequency

ZHANG Qingxia1， ?UKASZ Jankowski2

（1. School of Civil Engineering， Dalian Minzu University， Dalian 116600， China; 2. Smart-Tech Centre， Institute of Fundamental Technological Research， Polish Academy of Sciences， Warsaw 02-106， Poland）

Abstract： In civil engineering， the measured modal information in practice is less， and damage identification methods usually are sensitive to noise and require high accurate finite element models. Considering those problems， this paper proposes a structural damage identification method based on the correlation curves of moving masses and structural frequencies. Firstly， the mobile mass block is added on structure to obtain the relationship curves between its positions and the structural frequencies. Secondly， the approximate finite element model of the structure is established， and then the objective function is established to optimize the structural damages by calculating the correlation of the frequencies curve of the actual model and the approximate finite element model. Finally， The validity of the method is verified by numerical simulation of a simply supported beam with variable cross-sections. The results show that damage locations can be identified accurately even with large model errors， and the method has high applicability.

Keywords： structural health monitoring; damage identification; objective function; frequency

0 引言

結构损伤识别是健康监测系统的重要理论组成部分，为结构的预警、安全评定提供可靠的理论方法。结构动态响应中含有丰富的结构动力特性信息，是结构损伤识别的重要依据。

目前基于结构动态响应的损伤识别方法按照是否基于有限元模型分类，包括无模型和有模型两种方法。无模型的方法主要是基于动力指纹[1]和信号处理[2]的方法。无模型的方法不依赖于结构有限元模型，根据模态曲率或者响应信号分析能够快速判断或定位结构损伤的位置或者发生的时刻。但是这类方法由于没有有限元模型作为参考，一般较难对结构进行损伤定量的分析。

如果已知准确的未损伤结构的有限元模型，就可以结合结构实测模态信息，通过优化结构物理参数实现结构损伤的定位、定性和定量的分析。目前基于结构模态的损伤识别方法的研究有很多，但仍存在以下主要问题：1）工程实测中得到的模态数据信息量少，使损伤识别成为一个欠定问题;2）试验测量的模态信息往往对结构的局部损伤不够敏感[3]。为了解决上述问题，李大军等[4]提出在桥梁上附加质量测得结构的频率识别损伤的新方法。Zhong等[5]通过在原结构上移动附加质量得到系统的频率曲线，采用平稳小波分析判断梁裂纹位置。杨秋伟等[6]在原结构上附加已知的质量，形成新的结构形式，并测量出新结构的低阶频率值，结合原结构的频率信息进行损伤识别。周卫东等[7]通过在结构的某些部位附加已知的集中质量块，建立广义柔度灵敏度方程识别损伤参数。路平等[8]通过改变附加质量的大小、数目、位置来提高损伤识别精度。因此，在原结构上附加质量可提高测试数据量和提高结构损伤识别精度，是一种有效的方法。然而在实际工程中，往往很难建立准确的有限元模型，利用这样的有限元进行损伤识别，会出现损伤误判。

因此，针对无模型方法一般无法进行损伤定量分析，以及有模型方法往往对初始有限元模型精度要求较高的问题，本文借鉴附加质量方法的优点，提出一种基于质量-频率曲线相关性的目标函数，降低识别优化过程中对有限元模型精度的依赖，实现利用存在误差的有限元模型仍能较准确地识别结构损伤的位置和程度。

1 基于附加移动质量的损伤识别方法

1.1 附加移动质量

结构上附加质量后，结构的模态参数随之发生改变。如果质量附加在结构的不同位置，结构模态参数亦将不同。基于该思想，在结构不同位置上附加质量以获得充足的结构模态参数。如图1所示，首先在结构x1位置附加质量m，对结构进行模态测试，获得结构的n阶频率，分别记为ω1，1，ω2，1，···，ωn，1;然后将质量m移动附加到x2位置，测试结构模态，同样得到n階频率，分别记为ω1，2，ω2，2，···，ωn，2;以此类推，在梁上xk位置附加质量m时，获得对应的结构频率ω1，k，ω2，k，···，ωn，k。将试验获得的所有频率排列为矩阵ωm，如下式所示：

其中ωi，j表示在xj位置附加质量后的第i阶频率，则ωm可作为结构损伤识别的判别依据。

1.2 目标函数的建立

为了较准确地识别出结构的损伤位置和程度，往往需联合有限元模型进行优化识别。设所建立的有限元模型的质量矩阵和刚度矩阵分别为M和K。将结构划分为N个子结构，定义结构损伤因子为μ={μ1，μ2，···，μN}T，式中μi为第i个子结构损伤后与未损伤时的刚度的比值，即为第i个子结构的损伤因子。设第i个子结构的未损伤时扩展刚度矩阵为Ki，则损伤结构的刚度矩阵Kd（μ）可表示为

在理论有限元模型上的xj位置附加质量m，给定损伤因子为μ时，利用特征值分解可由附加质量后的结构刚度和质量矩阵计算出结构的频率，设第i阶频率为ωF（μ）。继而与实际中在结构x位置附加质量m后的实测频率进行比较，基于频率的相对误差建立目标函数，如下式所示：

通过优化损伤因子μ，使目标函数达到最小值的损伤因子即为识别的结构损伤。

利用式（3）优化识别损伤因子，一般需要准确的理论有限元模型。当实际工程中无法建立准确的有限元模型时，或者建立的有限元模型存在一定误差时，利用式（3）进行识别会影响损伤识别的精度。因此对式（3）进行改进，以降低目标函数对有限元模型精度的依赖性，如下式所示：

其中：

式（4）中ω?i为式（1）中矩阵ωm的第i列向量，物理意义为结构第i阶频率关于附加质量位置的曲线，ω?i（μ）为利用对应的有限元模型计算出来的第i阶频率关于附加质量的曲线。利用式（4）中的频率-质量曲线的相关性误差代替式（3）中的频率残差，有利于克服有限元模型不准确的问题。此外，结构未损伤时子结构损伤因子为1;当子结构发生损伤时，损伤因子小于1。式（4）中加入正则化项λ∥μ?1∥[9]，可限制优化过程中损伤因子在数值1附近。

2 数值模拟

2.1 简支梁模型

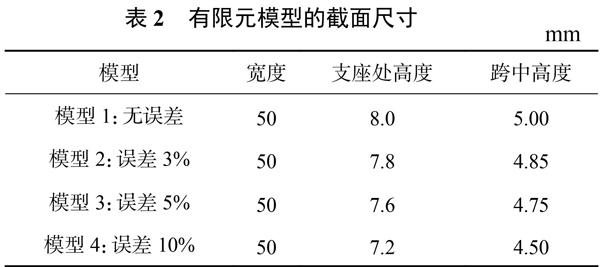
利用一变截面简支梁进行数值模拟，验证方法的有效性。如图2所示，简支梁长1m，截面下部成抛物线形式变化，支座处截面尺寸宽50mm、高8mm，跨中截面尺寸为宽50mm和高5mm，材料为钢材，其弹性模量为E=2.1×1011Pa，密度为ρ=7850kg/m3，泊松比为0.3。简支梁的有限元模型均匀划分为32个单元。横截面沿长度方向为变化的，因此每个单元的截面高度沿长度方向也是变化的，为简化计算，单元的截面高度取单元中点坐标位置的截面高度。

2.2 质量初选

结构上附加的质量若过小，则结构的频率改变较小，不能有效实现附加质量的目的;如果附加质量过大，实际工程操作中质量的移动和安装可能会比较费力，所以附加合适的质量是本文进行损伤识别的关键前提。首先初步选择在梁上分别附加质量块0.2，0.3，0.4kg;然后利用理论有限元模型计算结构上附加不同质量块时，结构前4阶固有频率随附加质量的变化曲线，如图3所示。由图可知结构的固有频率随着质量块质量的增大而减小;频率随着附加质量位置呈现类似周期变化规律，且阶数越高波数越大。通过观察图3，附加质量0.3kg后，频率的改变量约10%，频率改变量适中，所以附加质量选取0.3kg。

2.3 损伤工况

如图4所示，结构划分为8个子结构，其中每个子结构包含4个单元。采用刚度降低的方式模拟结构损伤，分析如下两种损伤工况：

1）工况1：单损伤情况，假设子结构3发生损伤，刚度降低30%，其损伤因子为0.7;其他子结构未损伤，损伤因子为1。

2）工况2：多损伤情况，子结构3和5的刚度分别降低30%、50%，即损伤因子分别为0.7和0.5;其他子结构未损伤，损伤因子为1。

利用有限元模型计算得到结构在未损伤以及两种损伤工况下的理论前4阶频率，如表1所示。

损伤工况1中，在相应的简支梁模型上附加0.3kg的质量块，质量块每次移动的间距为3.125cm（不包括支座处），故每阶频率可以获得31个关于附加质量位置的频率，如图5所示。图中“理论值”曲线为损伤工况1下利用有限元模型计算获得的频率关于附加质量位置的关系曲线;“考虑噪声”曲线为在“理论值”的基础上考虑1%随机误差，来模拟试验测试获得的频率曲线。由于利用结构响应识别频率的精度一般较高，本文频率只考虑到1%的误差已能满足实际情况。损伤工况2的频率曲线数据与工况1类似，这里不再一一列出。

2.4 目标函数的比较

本文考虑有误差的近似有限元模型进行结构损伤识别。设近似模型的几何尺寸误差分别取3%、5%和10%，根据设定误差，将变截面简支梁的支座处和跨中截面高度进行相应折减，具体建立的结构模型见表2，其中模型1为精确模型。

利用图5中的“考虑噪声”作为参考值，结合表2中的4个模型，分别利用两个目标函数（式（4）、式（3））进行损伤识别，MAC目标函数（式（4））和残差目标函数（式（3））识别的结构损伤结果如图6所示。

由图可知，对于模型1和模型2，即模型精准或模型误差较小时，利用MAC目标函数法和残差目标函数法都可以准确地判断3号子结构发生损伤;模型3和模型4情况下，随着模型误差的增大，利用MAC目标函数法（式（4））仍可以判断损伤位置，识别误差具有良好的稳定性和较高的容错率，而利用残差目标函数法（式（3））的识别误差较大。因此利用MAC目标函数可有效克服模型误差的影响，与实际工程相符，有利于损伤识别。

2.5 多损伤工况的损伤识别

考虑工况2中的多损伤工况，利用表2的4种有限元模型进行识别，识别结果如图7所示。从图中损伤识别结果可以看出，利用4种有限元模型均能准确地识别出子结构3和子结构5发生损伤，损伤程度与实际情况很接近。结果表明MAC目标函数法在模型误差较大时，仍然可以准确、有效地识别损伤位置和损伤程度，具有较高的

模型容错性。

3 结束语

本文通过在结构上附加移动质量获得频率-质量的关系曲线，并建立了关于曲线相关性的目标函数，最后利用变截面的简支梁模型验证了方法的有效性和鲁棒性，得到以下结论：

1）通过在结构上布置移动质量可以获取更多的结构频率信息，解决了试验中实测结构频率信息少的问题。

2）利用MAC目标函数法可以有效降低识别方法对有限元模型准确性的依赖，损伤识别精度高，具有较高的误差容错性。

参考文献

[1]尚鑫.基于动力测试的桥梁损伤识别研究[D].西安：长安大学，2014.

[2]罗裴，姜德生，郭丹.小波包多尺度分析在智能复合材料板损伤检测中的应用[J].中国测试技术，2006（3）：48-50.

[3]冯新，李国强，周晶.土木工程结构健康监测诊断中的损伤伤识别方法综述[J].地震工程与工程振动，2005，25（2）：105-113.

[4]李大军，霍达，韩强.桥梁损伤的移动质量多次测量检测法[J].华南理工大学学报（自然科学版），2005（4）：50-52.

[5] ZHONG S， OYADIJI S. Analytical predictions of natural frequencies of cracked simply supported beams with a stationary roving mass[J]. Journal of Vibration and Vibration， 2008， 311（1）： 328-352.

[6]楊秋伟，刘济科.结构损伤识别的附加质量方法[J].工程力学，2009，26（5）：159-163.

[7]周卫东，杨秋伟，赵卫.基于广义柔度和附加质量的结构损伤识别方法研究[J].机械强度，2016，38（1）：156-159.

[8]路平，王龙，段静波，等.基于附加质量的梁损伤识别影响因素分析[J].解放军理工大学学报（自然科学版），2017（3）：295-301.

[9] TITURUS B， FRISWELL M. Regularization in model updating[J]. International Journal for Numerical Methods in Engineering， 2008， 75（4）： 440-478.

（编辑：商丹丹）