基于改进共轭梯度的大规模多输入多输出预编码

白鹤 刘紫燕 张杰 万培佩 马珊珊

摘 要：针对大规模多输入多输出（Massive MIMO）系统下行链路预编码实现复杂、线性预编码矩阵求逆困难等问题，提出一种基于对称逐步超松弛预处理共轭梯度法（SSOR-PCG）的低复杂度预编码算法。该算法在共轭梯度（PCG）算法的基础上，采用对称逐步超松弛分裂（SSOR）算法对矩阵进行预处理以降低矩阵的条件数，达到提高预编码算法收敛速度、降低复杂度的目的。仿真结果表明：与PCG算法相比，所提出的SSOR-PCG预编码算法运行时间缩短约88.93%，在信噪比为26dB时已收敛;与迫零预编码算法相比，所提算法迭代2次即可获得与迫零预编码算法相近的系统容量性能，复杂度降低约一个数量级，误码率降低约49.94%。

关键词： 大规模多输入多输出;线性预编码;共轭梯度;对称逐步超松弛

中图分类号：TP391.9

文献标志码：A

Abstract：To solve the problems of high complexity of precoding and difficulty of linear matrix inversion in downlink Massive Multi-Input Multi-Output （Massive MIMO） system， a precoding algorithm based on low-complexity Symmetric Successive Over Relaxation Preconditioned Conjugate Gradient （SSOR-PCG） was proposed. Based on preconditioned Conjugate Gradient Precoding  （PCG） algorithm， a Symmetric Successive Over Relaxation （SSOR） algorithm was used to preprocess the matrix to reduce its condition number， accelerating the convergence speed and the decreasing the complexity. Simulation results demonstrate that compared with PCG algorithm， the proposed algorithm has running time of around 88.93% shortened and achieves convergence when the Signal-to-Noise Ratio （SNR） is 26dB. Furthermore， compared to zero-forcing precoding algorithm， the proposed algorithm requires only two iterations capacity-approaching performance，the overall complexity is reduced by one order of magnitude， and the bit error rate is decreased by about 49.94%.Key words： Massive Multi-Input Multi-Output （Massive MIMO）; linear precoding; conjugate gradient; Symmetric Successive Over Relaxation （SSOR）

0 引言

大规模多输入多输出（Massive Multi-Input Multi-Output， Massive MIMO）技术作为5G的关键技术之一，由于其具有容量大、频谱效率高等特点而受到学者广泛关注[1]。预编码技术不仅可以提高信道容量、降低誤码率和简化接收机，还能满足用户对高速率数据传输的需求，对提升5G系统性能起到重要作用。

线性预编码算法[2]因其算法复杂度低且容量性能接近非线性预编码算法而被广泛使用，其基本原理是发射端在已知信道状态信息（Channel State Information， CSI）的前提下对发送信号进行线性预处理，消除用户间干扰，便于接收端信号检测，提高系统容量。传统线性预编码算法主要包括迫零（Zero Forcing， ZF）预编码、最小均方误差（Minimum Mean Squared Error， MMSE）预编码以及匹配滤波器（Matched Filter， MF）预编码等[3]。随着天线数目的不断增加，线性预编码算法求逆困难，系统复杂度呈指数形式增长。

为了解决线性预编系统复杂度高等问题，研究者以ZF算法矩阵求逆重点研究如何降低预编码算法实现复杂度。文献[4]采用纽曼级数（Neumann Series， NS）方法对矩阵进行求逆，该方法从工程应用角度来说更易实现;但其复杂度高于直接对矩阵进行逆运算。文献[5]采用理查德森算法（Richardson Method， RM）来降低预编码实现的复杂度，该算法通过迭代运算代替矩阵求逆，可以有效降低系统复杂度;但是其收敛速度取决于松弛因子的选取。随着天线数目的不断增加，下行信道矩阵信道向量渐进正交，文献[6]利用正定Hermitian矩阵的特性，提出基于高斯赛德尔（Gauss-Seidel， GS）算法的预编码方案。该算法以迭代方式逐渐近似ZF预编码的系统容量性能，不需要矩阵求逆。

文献[7]采用对称逐次超松弛（Symmetric Successive Over Relaxation， SSOR）算法将正定Hermitian矩阵分解为对角阵、严格的上三角阵和严格的下三角阵，通过对称的方式计算逐步超松弛（Successive Over Relaxation，SOR）算法，有效提高了算法收敛速率，降低了系统复杂度。为了解决线性预编码矩阵求逆困难、算法复杂度高等问题，本文提出一种基于改进共轭梯度（Conjugate Gradient Precoding， PCG）算法的SSOR-PCG预编码算法，该算法在CG算法的基础上，采用SSOR分裂算法对矩阵进行预处理来降低矩阵运算的条件数，以达到提高预编码算法收敛速度、降低系统复杂度的目的。

1 大规模多输入多输出系统模型

搭建一个单小区多用户大规模多输入多输出下行链路系统模型，假设该模型工作在FDD模式，基站端配备M根天线，接收端配备K根天线，其中MK。假设接收端的用户均为单天线用户且满足等功率分配条件，基站端可以获得完全信道状态信息[8]。则下行链路接收信号y可以表示为：

其中： y∈RK*1为K个用户获得的总接收信号;hK∈RM*1为从基站端到用户K的信道矢量;n～CN（0，IK）为AWGN噪声。x～RM*1为基站端M根天线的发送信号，可以表示为：

由于信道矩阵具有渐进正交性，文献[10]已经证明当基站端天线数目接近于无穷时，ZF预编码的系统容量无限趋近脏纸预编码（Dirty Paper Precoding，DPC）的系统容量。ZF预编码算法通常需要对预编码矩阵W进行逆运算求解，由于大规模多输入多输出系统中基站端天线数目庞大，导致ZF预编码矩阵的求逆过程十分复杂，其计算复杂度描述为O（K3）。

2.2 共轭梯度预编码算法

共轭梯度法（Conjugate Gradient， CG）的基本思想是将共轭法与最速下降方法相结合，使用已知的梯度方向构建共轭方向，并沿方向搜素目标函数的最小值。共轭梯度算法具有二次终止性，不需要进行矩阵存储操作，既能改善最速下降法收敛速度慢的缺点，又能解决牛顿法需要计算Hesse矩阵逆的问题。

文献[11]指出大规模多输入多输出系统中信道矩阵H是满秩矩阵，当且仅当q是一个零向量时qH的值才为零。对于所有的非零向量q，都满足qPqH>0，因此矩阵P是Hermitian正定矩阵，在大规模多输入多输出系统中可以采用CG算法求解方程组Pt=s的解。

2.3 SSOR-PCG预编码算法

虽然CG算法相较于ZF算法复杂度更低，但是当Hermitian正定矩阵的条件数取值较大时，CG算法的迭代次数会增多，因此可以使用PCG算法以达到减小迭代次数的目的。PCG算法的基本思想为：通过对Hermitian正定矩阵P进行预处理来减少系数矩阵的条件数，从而提高CG算法的收敛速度[12]。

PCG算法的重点是如何选择合适的预处理矩阵C。通常预处理矩阵的选择需要满足以下几个条件：

1）预处理矩阵C应该为对称正定矩阵;

2）预处理矩阵C应该与Hermitian正定矩阵P具有相似性;

3）预处理Hermitian正定矩阵的特征值应该尽量集中，即cond（）≈1尽可能小;

4）预处理后的线性方程应易于求解。

利用SSOR分裂算法將Hermitian正定矩阵P分裂为以下三部分：

其中：BJ=D-1（L+LH）为雅克比（Jacobi）迭代算法的迭代矩阵; ρ（BJ）为Jacobi迭代矩阵的谱半径。由2.2节可知P=HHH，在快速变化的时变信道中P值不是恒定的，因此需要不断计算最优松弛因子ωopt的值。通常需要执行两次SOR算法才能获得最佳ωopt值，在大规模多输入多输出通信系统中计算其最优松弛因子十分困难，鉴于此，有学者提出通过简单数学变换来确定松弛因子的近似最优值。对于瑞利衰落信道矩阵H而言，P=HHH+ζIK的对角线元素pkk（k=1，2，…，K）服从2M自由度卡方分布[14]。 根据文献[15]，通过切比雪夫不等式变换，得到：

式（18）中当M的取值接近无穷大时，式（1-ε）M < pkk < （1+ε）M的值近似为1。大规模多输入多输出系统中基站配备的M根天线可以近似表示为pkk，因此对角矩阵D-1可以近似表示为I/M，式（17）可以变为：根据随机矩阵的相关理论，当M和K的值足够大且M/K的值接近固定时，矩阵P的最大谱半径，即其最大奇异值可以表示为：

由式（22）可知，最优松弛因子的近似最优值opt仅取决于大规模多输入多输出系统中基站的天线数M和移动端用户数K。由文献[16]可知只有当0<ω<2时，SSOR算法才具有收敛性，其中最优松弛因子范围满足1<ω<2，即用户数与天线数的比值位于[0.051，0.171]。由于SSOR算法较SOR算法而言对松弛因子变化不敏感，所以SSOR算法采用最优松弛因子的近似最优值就可以确保获得良好的系统性能。

3.2 复杂度分析

根据2.3节SSOR-PCG算法伪代码可知，获取αk需要1×K的rTk和K×1的rk相乘，以及1×K的mTk、K×K的C-1P和K×1的mk相乘，因此计算αk需要K2+2K次乘法;同理，计算tk+1需要K次乘法;计算rk需要K2+K次乘法;计算bk需要2K次乘法;计算mk+1需要K次乘法。综上所述，SSOR-PCG算法每迭代一次需要O（2K2+7K）的复杂度。

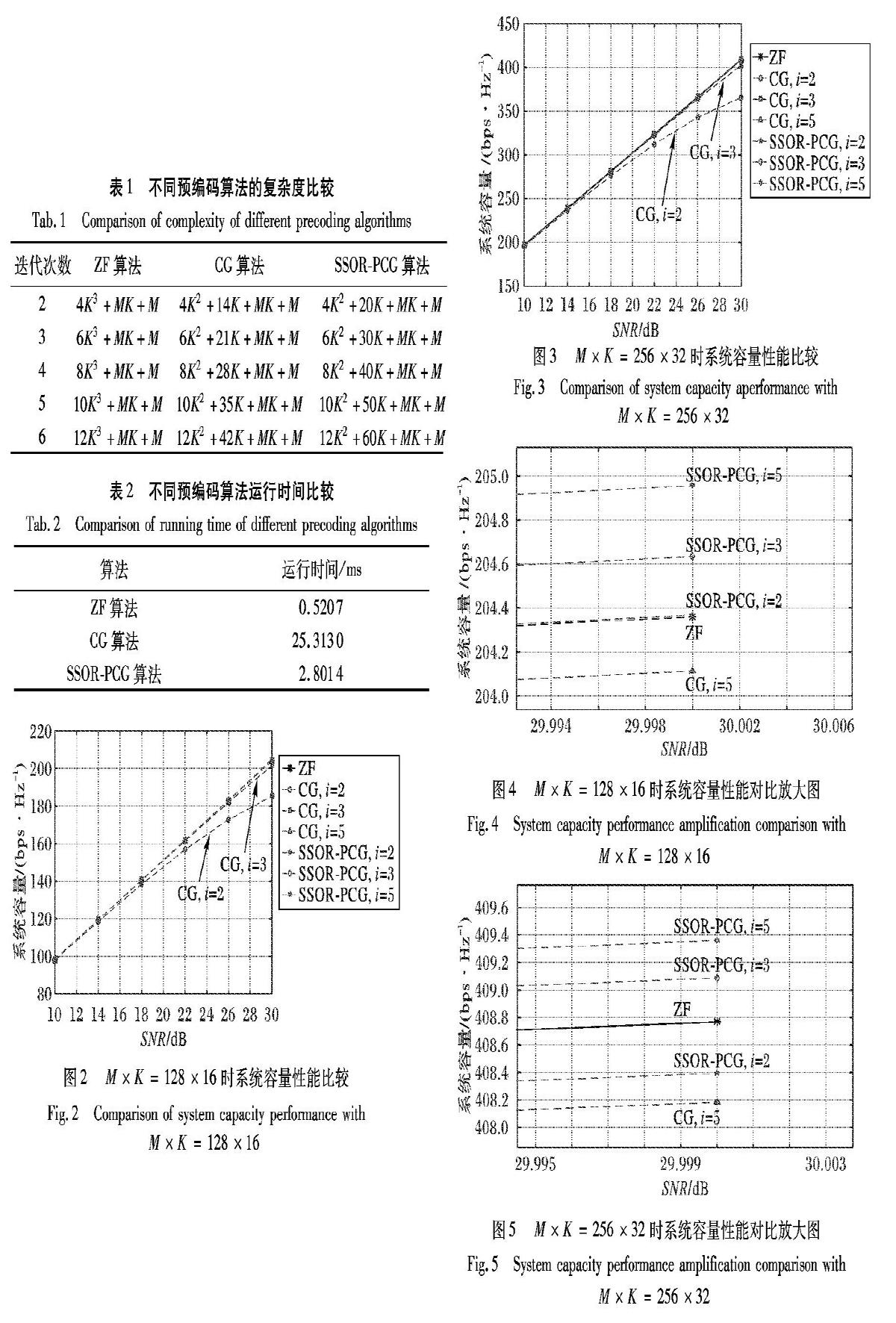
根据式（2）、（3）可知，大规模多输入多输出系统中x的获取需要M×K的H和K×1的s相乘，因此计算x需要MK次乘法;同理，x与归一化因子β相乘需要M次乘法。综上所述，SSOR-PCG算法复杂度为（2K2+7K）i+MK+M。文献[17]表明CG预编码算法每迭代1次需要执行2K2+10K次乘法，其算法复杂度为（2K2+10K）i+MK+M。表1为不同迭代次数下ZF算法、CG算法和SSOR-PCG算法的复杂度。表2是三种不同预编码算法的运行时间。实验结果表明，ZF预编码算法复杂度约为3个数量级，且算法运行时间最短。CG预编码算法和SSOR-PCG预编码算法复杂度约为2个数量级，同ZF预编码算法相比，复杂度降低约1个数量级。在算法复杂度数量级相同的情况下，本文所提SSOR-PCG预编码算法相较于CG算法运行时间缩短约88.93%。

4 仿真结果及分析

[5] TRIFAN R， ENESCU A. MU-MIMO precoding performance conditioned by inter-user angular separation[C]// Proceedings of the 2018 International Symposium on Electronics and Telecommunications. Piscataway： IEEE， 2018： 1-4.

[6] FENG M， XU Y. Low-complexity linear precoding for pilot contamination mitigation in multi-cell massive MIMO systems[C]// Proceedings of the 2017 International Symposium on Intelligent Signal Processing and Communication Systems. Piscataway： IEEE， 2017： 807-811.

[7] LU Z， NING J， ZHANG Y， et al. Richardson method based linear precoding with low complexity for massive MIMO systems[C]// Proceedings of the IEEE 81st Vehicular Technology Conference. Piscataway： IEEE， 2015： 1-4.

[8] NAM J， ADHIKARY A， AHN J， et al. Joint spatial division and multiplexing： opportunistic beamforming， user grouping and simplified downlink scheduling[J]. IEEE Journal of Selected Topics in Signal Processing， 2014， 8（5）： 876-890.

[9] JU M， QIAN J， LI Y， et al. Comparison of multiuser MIMO systems with MF， ZF and MMSE receivers[C]// Proceedings of the 2013 IEEE Third International Conference on Information Science and Technology. Piscataway： IEEE， 2013： 1260-1263.

[10] QIN X， YAN Z， HE G. A near-optimal detection scheme based on joint steepest descent and Jacobi method for uplink massive MIMO systems[J]. IEEE Communications Letters， 2016， 20（2）： 276-279.

[11] XIE T， HAN Q， XU H， et al. A low-complexity linear precoding scheme based on SOR method for massive MIMO systems[C]// Proceedings of the IEEE 81st Vehicular Technology Conference. Piscataway： IEEE， 2015： 1-5.

[12] 曲桦， 梁静， 赵季红， 等. 基于SOR-PCG的低复杂度信号检测算法研究[J]. 电视技术， 2016， 40（8）： 99-102， 117. （QU H， LIANG J， ZHAO J H， et al. Study on low-complexity signal detection based on successive over relaxation-preconditioned conjugate gradient method [J]. Video Engineering， 2016， 40（8）： 99-102， 117.）

[13] XIE T， DAI L， GAO X， et al. Low-complexity SSOR-based precoding for massive MIMO systems[J]. IEEE Communications Letters， 2016， 20（4）： 744-747.

[14] 杨伟茜. Massive MIMO系统中低复杂度预编码算法研究[D]. 赣州： 江西理工大学， 2018：41-48. （YANG W Q. Research on low-complexity precoding algorithm in Massive MIMO system[D]. Ganzhou： Jiangxi University of Science and Technology， 2018：41-48.）

[15] 朱庆浩. 大规模MIMO系统预编码算法的研究与优化[D]. 赣州： 江西理工大学， 2018：27-30. （ZHU Q H. Research and optimization of precoding algorithm for large-scale MIMO systems[D]. Ganzhou： Jiangxi University of Science and Technology， 2018：27-30.）

[16] 张弛. 大规模MIMO系统低复杂度预编码算法研究[D]. 南京： 東南大学， 2018：20-35. （ZHANG C. Research on low-complexity precoding algorithm of large-scale MIMO system[D]. Nanjing： Southeast University， 2018：20-35.）

[17] 任彦. 大规模MIMO预编码算法的研究[D]. 成都： 西南交通大学， 2017：30-42. （REN Y. Research on large-scale MIMO precoding algorithm[D]. Chengdu： Southwest Jiaotong University， 2017：30-42.）

[18] 李婉婉. 大规模天线系统中的预编码及相关技术研究[D]. 成都： 电子科技大学， 2018：14-16. （LI W W. Research on precoding and related technologies in large-scale antenna systems[D]. Chengdu： University of Electronic Science and Technology of China， 2018：14-16.）