基于异构多核平台低能耗周期任务调度算法

夏军 袁帅 杨逸

摘 要：针对异构多核平台存在的高能耗问题，提出一种运用优化理论求解周期任务最优能耗分配方案的算法。该算法对周期任务的最优能耗问题进行建模，并对模型添加限制条件。根据优化理论将二进制整数规划问题松弛化后得到凸优化问题，通过内点法求解优化问题并得到松弛化的分配矩阵，对分配矩阵进行判决处理后得到部分任务的分配方案。在此基础上，通过迭代的方式求得剩余任务的分配方案。实验结果表明，该分配方案产生的能耗与同类优化理论算法相比能耗降低约1.4%，

与能耗相当的优化理论算法相比执行时间减少86%，且仅比理论最优能耗值高2.6%。

关键词：多处理器;节能调度;周期任务;利用率;优化理论

中图分类号：TP316.2

文獻标志码：A

Abstract： Concerning at the high energy consumption of heterogeneous multi-core platforms， an algorithm for solving the optimal energy allocation scheme of periodic tasks by using optimization theory was proposed.The optimal energy consumption problem of periodic tasks was modeled and added constraints to the model.According to the optimization theory， the binary integer programming problem was relaxed to obtain the convex optimization problem. The interior point method was used to solve the optimization problem and the relaxed distribution matrix was obtained. The allocation scheme for partial tasks was obtained after the judgement processing of the decision matrix. On this basis， the iterative method was used to find the allocation scheme for the remaining tasks. Experimental results show that the energy consumption of this distribution scheme is reduced by about 1.4% compared with the similar optimization theory algorithm， and compared with the optimization theory algorithm with the similar energy consumption， the execution time of this scheme is reduced by 86%. At the same time， the energy consumption of the scheme is only 2.6% higher than the theoretically optimal energy consumption.Key words：  multiprocessor; energy saving scheduling; periodic task; utilization rate; optimization theory

0 引言

随着嵌入式系统复杂度和性能要求的提升，多处理器片上系统（System on Chip， SoC）得到了广泛的应用，同时，如何降低系统产生的高能耗成为社会关注的焦点。所以，在多处理器片上系统中能耗优化技术起到了重要的作用。在现有平台中，处理器核心大多嵌入动态电压频率调节（Dynamic Voltage Frequency Scaling， DVFS）技术和动态电源管理（Dynamic Power Management， DPM）技术。DPM负责管理系统产生的静态功耗，当处理器处于空闲状态时，该技术将处理器工作模式切换到低功耗状态。但是，DPM切换处理器状态需要时间并产生一定的能耗。对于周期性任务来说，频繁地切换处理器的工作状态所产生的能耗不可以忽略。

DVFS调度技术则负责管理系统产生的动态功耗，利用处理器工作频率和功耗之间的凸关系，降低处理器核心工作频率已达到减小能耗的目的，同时延长执行时间，减少处理器的空闲状态，从而可以减小处理器状态切换带来的能耗。

随着计算系统架构的发展，DVFS调度技术已经从单核处理器DVFS调度技术[1-3]，

发展到多核/多处理器DVFS调度技术[4-6]，而多核/多处理器DVFS调度技术从同构多核/多处理器DVFS调度技术发展到异构多核/多处理器DVFS调度技术[7-8]。根据应用于实时系统和非实时系统的差异进行分类，DVFS调度技术可以分为基于实时系统的DVFS调度技术[9-10]和基于非实时系统的DVFS调度技术。

在异构多核平台实时系统DVFS调度技术中，启发式算法使用较为广泛。文献[11]中针对帧任务提出了min-min启发式算法，该算法首先计算未分配任务的最小完成时间，然后选择预期完成时间最小的任务分配给对应的处理器;文献[12]中提出了max-min启发式算法，该算法与min-min区别在于计算完任务最小完成时间后，将预期完成时间最大的任务分配给相应的处理器，优点在于保证了平台的负载均衡。启发式算法能够快速地得到处理器的任务分配方案，但是算法产生的能耗较大。文献[13]中针对周期任务提出了最大本地剩余执行时间优先（Largest Local Remaining Execution Time First， LLREF）算法，根据任务剩余时间对各个处理器核心分配任务，但频繁的算法调用和任务迁移同样产生了巨大能耗。

近年来，基于优化理论的算法已经运用到DVFS任务调度技术中。文献[14]中将多处理器任务调度问题表示为无限维最优控制问题，建立了三种优化理论模型，但没有对模型进行详细的求解;同时还提出了可调度性算法的概念，如果算法产生的任务分配方案没有超过任务截止期限的情况出现，即满足可调度性条件。

文献[15]中提出了基于松弛简单取整算法（Relaxation-based Naive Rounding Algorithm， RNRA），并在此基础上提出了基于松弛的迭代取整算法（Relaxation-based Iterative Rounding Algorithm， RIRA），两种算法假设不同任务在不同处理器的执行效率不同，对最小处理器能耗问题建立凸优化模型，并运用优化理论求解最优能耗问题。这类算法虽然产生的能耗较低，但是算法复杂度较高，求解时间较长，而且没有考虑算法可调度性条件，使得算法求解结果可用价值不高。

本文针对周期任务调度算法存在的问题，提出了减少迭代算法（Decrease Iteration Algorithm， DIA）。该算法对周期任务最小能耗问题建立模型，通过限制处理器的利用率以提高算法的可调度性，对模型求解结果进行判决处理，得到部分任务的分配方案。剩余任务根据平均任务密度排序后，重新定义能耗模型，优先分配密度较大的任务，通过这种方式，算法产生的能耗接近理论最优值，不仅能够更快地得到所有任务的分配结果，而且能提高算法的可调度性。

1 系统模型

1.1 任务模型

1.2 平台模型

假设多处理器片上系统（SoC）有m个异构处理器，记为Ψ={Ψ1，Ψ2，…，Ψm}，所有的处理器均可利用DVFS技术动态调节电压/频率。定义sji∈（0，1]为任务Ti在处理器Ψ j上的执行速率，对应的WCET可表示为Ci/（sjif）。假定m个异构处理器核心为理想的处理器核心，其频率范围在（0， fmax）连续可变。

1.3 功耗模型

处理器采用互补金属氧化物半导体（Complementary Metal Oxide Semiconductor， CMOS）工艺制造的SoC，每个核心具有独立的DVFS功能，

其每个处理器核心的功耗由三个部分组成：1）动态功耗，记为Pdynamic;2）静态功耗，记为Pstatic;3）固有功耗，记为Pon。

假定在SoC中有m个异构处理器核心，其处理器核心的总功耗的表达式为：处理器的动态功耗可以近似表达为：

其中：  β j为与Ψ j设计和工艺相关的常量值。

文献[9]的研究表明，当功耗函数为凸函数时，恒定频率产生的能耗优于时变频率的，所以本文功耗模型只考虑恒定频率，不考虑时变频率。由于Pon在SoC中对于所有异构核心都是统一依赖的，只有当系统所有核心和外部电路都没有工作时，可以利用DPM技术进行关闭，Pon的最小化问题不属于本文研究范畴，故本文不讨论固有功耗。

另外，当Ψ j处于普通的激活模式时，P jstatic对于整个系统功耗贡献比例相对于动态功耗来说非常小，同时任务集的分配问题对P jstatic的影响也非常小，因此本文假定采用如下简化的功耗函数：

本文采用文献[16-17]中处理器核心功耗模型，假定所有异构处理器核心有两种工作模式：1）激活模式。在该模式下功耗函数符合式（2）定义。2）空闲模式。该模式下所有功耗为0。

某个处理器在激活模式下执行任务，当没有任务执行时，立即从激活模式进入空闲模式。

由于这种模式间转换的能耗开销与处理器上执行完成任务的功耗相比非常小，因此假定这部分的开销已经包含在任务执行的过程之中。

1.4 问题定义

给定一组实时周期任务集T={T1，T2，…，Tl}，将任务分配到m个异构处理器核心，使得任务不超过截止期限的条件下所有处理器产生的总能耗最小。设任务集Ti对应的最坏情况执行指令周期集合为C={C1，C2，…，Cl}，由于处理器核心的异构特性，同一任务在不同的处理器的执行效率不同，定义任务的执行速率矩阵：矩阵的元素值1表示任务已分配，0表示任务未被分配。假设xji=1，矩阵行向量表示任务Ti分配到处理器核心Ψ j。

由于系统产生的功耗和处理器工作频率的三次方成正比关系，当处理器的工作频率下降，任务的执行时间变长。系统的能耗可表示为处理器功耗与执行时间的乘积（E=Pt），因此，为了使系统产生尽可能小的能耗，系统的工作频率和时间需要达到一种平衡。同时为了满足任务实时性的条件，任务的完成时间不得超过截止期限Di。通过求解分配矩阵A和处理器工作频率fM，最后得到系统的最小能耗E。

2 任务分配算法

2.1 问题分析

任务集T={T1，T2，…，Tl}在0时刻同时释放，任务数大于处理器核心数（l>m），总存在处理器核心执行多个任务，为了确保其执行先后顺序，定义任务Ti在m个处理器以最大频率fjmax工作时的平均任务密度（Average Task Density， ATD）为：

式（6）对处理器的工作频率fj进行归一化处理（fj= fjreal/fjmax），此时的工作频率为1。对任务的平均执行时间进行降序排列ATDi1≥ATDi2≥…≥ATDil，排序后的任务集为T={Ti1，Ti2，…，Til}。平均任务密度的大小代表任务的执行需求不同，平均任务密度越大，系统执行任务产生的能耗越大。由满足负载均衡的任务分配方法得到启发，在分配时优先分配平均任务密度较大的任务。

为了使系统产生最小能耗并且滿足任务不超过截止期限的条件，由文献[18]可知，每个处理器核心中任务的利用率之和要无限接近1，如式（7）所示。从而，每个处理器核心中任务的利用率之和不大于1可作为算法可调度性标准。

对于式（13）描述的最优能耗的任务分配问题属于二进制整数规划问题，求解难度较大。在最优理论中，整数线性规划问题的可行域是其松弛问题的子集。所以，为了方便得出最优解，在这里需要重新定义分配矩阵。将分配矩阵A松弛化后得到：

2.2 求解算法

通过内点法求得松弛化的分配矩阵，分配矩阵中的元素值在[0，1]中连续，然而最终的分配结果有如下条件：

由于松弛问题的最优解不一定是整数规划问题的最优解，为了尽可能得到接近理论最优能耗的分配矩阵，RNRA对分配矩阵进行简单处理，将每行元素最大者判为1，其余元素判为0，由式（7）可知，此方法会变相放大分配元素x值而导致处理器核心利用率大于1。为了避免此问题出现，本文算法首先对矩阵中的元素进行门限判决，大于门限值Δ判为1，小于门限值则判为0。当k个任务完成分配，分配矩阵可以分解为已分配矩阵A*1和未分配矩阵A*2两个矩阵。

由此得出部分任务的分配方案，并通过式（19）计算每个处理器核心的利用率，在分配的过程中保证每个处理器核心的利用率Uj≤1是分配的前提，利用率超出1分配方案将不满足实时性的条件。

接下来求解分配矩阵A*2。对于未分配任务，在确定分配方案之前，先根据任务的ATD进行降序排列。这里采用文献[15]中RIRA的思路，先固定部分任务分配方案，得到每个处理器核心的利用率后，最优能耗模型更新为式（20），求解剩余的任务分配方案。

将A*2的首行元素值最大值判为1，剩余元素值判为0，剩余行元素判为0，将未分配矩阵首行元素增加到已分配矩阵中。已分配任务矩阵和未分配任务矩阵得到更新，优化能耗模型同样再次更新。运用同样的方式，进行多次迭代求解所有任务的分配方案。

3 仿真实验及结果分析

通过设置一系列仿真实验评估算法的调度能力，同时把本文算法与RIRA、RNRA的归一化能耗（即算法能耗值与理论最优值的比值）、利用率大于1次数（可调度性）和算法执行时间进行对比。所有的仿真实验在Matlab 2018a中实现，操作系统为Windows 10家庭中文版，版本为1803，处理器是lntel Core i5-8265U CPU @ 1.6GHz 1.8GHz。

仿真实验模拟24个周期任务分配到6个处理器核心中。任务的周期是一定范围内的随机值，24个任务周期的均值为100。为了验证不同的任务周期范围对算法调度能力的影响，在实验中设置5种周期范围，分别为[50，150]、[60，140]、[70，130]、[80，120]、[90，110]。根据参考文献[15]中生成帧任务集的方式，设置4组不同的WCEC范围，每种范围生成100组随机任务。门限值Δ设置为0.99。

通过控制变量的方式，设置2组实验评估任务元素变化对算法归一化能耗、利用率大于1次数和算法执行时间的影响。

实验1 同一任务集设置不同的周期范围。

为了验证DIA在不同任务周期下的调度能力，任务集设置以下参数：

1）随机生成5种范围的周期，每种100组，每组中有24个随机数对应到24个任务的周期，周期的均值为100。由于算法需要得出24个任务的最小公倍数即超周期，为了防止超周期过大而导致计算不准确，对超周期进行筛选，把每个任务的周期数值精确到个位，超周期最大不差过109。

2）WCEC范围选择[10，15]，生成一个24×6矩阵，矩阵中的元素值为[0.1，1]范围内的随机数，表示24个任务在不同处理器的执行速率，根据公式Ci/（sji f）得到任务在各个处理器的最坏情况执行时间WCET。

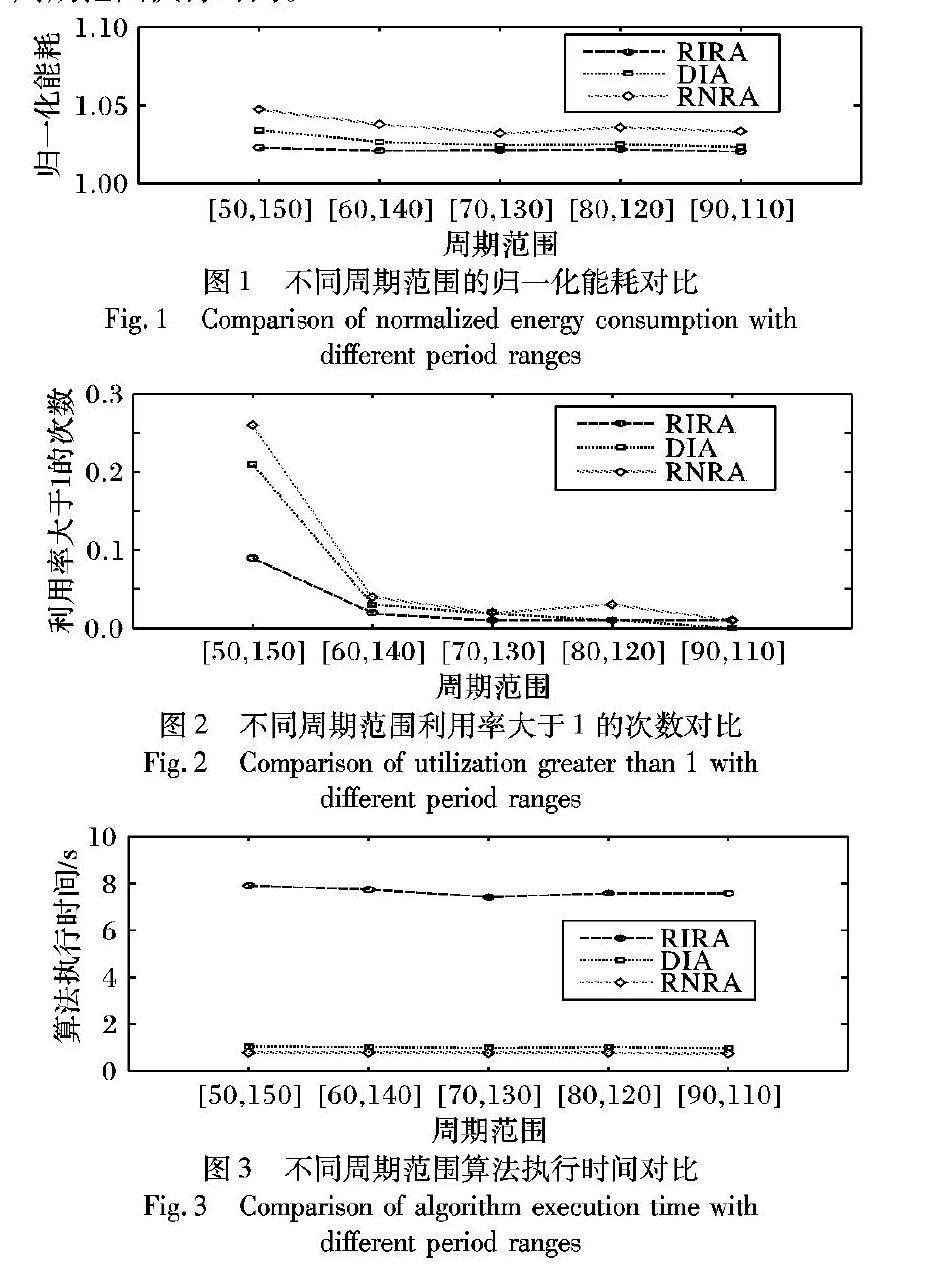
实验结果如图1～3所示：图1中把每种周期范围100组任务的能耗值取平均，然后与理论最优能耗值相比;图2是平均每组任务超过截止期限的次数;图3表示每种算法在不同周期范围执行时间。

由图1可知，三种算法在不同周期范围内的归一化能耗波动较小，都很接近理论最优能耗，随着周期宽度的下降，能耗值略微下降。DIA与RNRA相比，前者的归一化能耗比后者平均优化1.1%，当周期范围是[50，150]，DIA比RNRA优化1.4%，效果达到最好。在5种周期范围，DIA能耗最接近RIRA，RIRA略小于DIA，平均约小0.5%。然而，在图3中，RIRA与其他算法执行时间差距较大，DIA平均执行时间为1.02s，RNRA执行最小，平均为0.85s，RIRA的执行时间较长，平均为7.65s。从图2可以看出，三种算法随着周期范围的变窄，利用率大于1的次数逐渐在减少，DIA在周期范围[90，110]时没有处理器核心利用率大于1的次数出现，完全避免了任务超过截止期限的情况。RNRA超过利用率次数1的次数最多。

由實验1可以得出，DIA在归一化能耗方面接近于理论最优值，只比RIRA稍高0.7%，但是在算法执行效率方面得到了大幅优化，同时在超出截止期限次数方面也得到了明显的减少。DIA能够拥有RIRA和RNRA的优点，在减小能耗的同时降低算法的执行时间，能够在更短的时间内获得有效的分配方案。

实验2 固定周期设置不同的WCEC范围。

为了验证DIA对不同负载任务的调度能力，任务集设置以下参数：

1）设置100组周期范围为[80，120]的任务集，每组生成24个随机数对应24个任务的周期，每组任务集周期的均值为100。与实验1相同，过滤掉较大的超周期。

2）设置4种WCEC范围，任务设置1的WCEC范围为[1，5]，任务设置2的WCEC范围为[5，10]，任务设置3的WCEC范围为[10，15]，任务设置4的WCEC范围为[15，20]， WCEC生成方式同实验设置1，每种WCEC范围生成100组任务集。

表1为各算法不同任务设置的归一化能耗。RNRA归一化能耗表现最差，DIA在[1，5]、[5，10]、[10，15]三种WCEC范围中的归一化能耗略高于RIRA，当WCEC范围是[15，20]时，DIA能耗值优于RIRA约0.6%，仅仅比理论最优值高1.8%。三种算法在[1，5]、[5，10]两种范围的WCEC中都没有出现利用率大于1的情况。当WCEC为[10，15]时，DIA处理器核心的利用率没有超过1的情况，算法的可调度性为100%;而RIRA和RNRA表现较差。在算法执行时间方面，三种算法波动较小，RNRA执行时间最短约为0.87s，其次DIA为0.96s，RIRA表现最差为7.84s。

由实验2可知，DIA调度不同负载任务的能耗值接近RIRA，随着任务负载的加大，DIA与RIRA的差距逐渐缩小，在WCEC范围为[10，15]时产生优于RIRA的能耗。

在算法执行时间方面，DIA大幅度领先RIRA，能够在更短的时间完成任务调度，同时产生更低的能耗。在可调度性方面，DIA优于RNRA和RIRA，在中低负载情况下算法可调度性达到100%。

4 结语

本文针对异构多核平台中的非抢占式周期任务提出了减少迭代算法DIA。該算法首先对周期任务的最小能耗问题进行建模，每个处理器利用率不超过1作为模型的限制条件，运用优化理论求解最小能耗问题，对求解结果通过判决门限进行初步处理后得到部分任务的分配结果，在此结果基础上通过迭代的方式动态求解剩余任务的分配方案。实验结果表明，DIA得到的分配方案产生的能耗更加接近理论最优值，节能效果略优于已有算法，但是算法的执行时间比现有算法大幅减少。

由于处理器利用率不大于1这一限制条件的存在，提高了算法可调度性，使得任务调度更加满足实时性的条件。在未来，笔者将对算法进行改进，使得算法能耗更加接近理论最优值的同时，不仅减少当处理器负载较高时任务分配方案超过截止期限的次数，而且进一步减少算法迭代次数，使得算法能够在更短的时间内完成任务的分配。

参考文献（References）

[1] NIELSEN L S， NIESSEN C， SPARSO J， et al. Low-power operation using self-timed circuits and adaptive scaling of the supply voltage[J]. IEEE Transactions on Very Large Scale Integration Systems， 1994， 2（4）： 391-397.

[2] BURD T D， PERING T A， STRATAKOS A J， et al. A dynamic voltage scaled microprocessor system[J]. IEEE Journal of Solid-State Circuits， 2000， 35（11）： 1571-1580.

[3] NOWKA K J， CARPENTER G D， MACDONALD E W， et al. A 32-bit powerpc system-on-a-chip with support for dynamic voltage scaling and dynamic frequency scaling[J]. IEEE Journal of Solid-State Circuits， 2002， 37（11）： 1441-1447.

[4] SEO E， JEONG J， PARK S， et al. Energy efficient scheduling of real-time tasks on multicore processors[J]. IEEE Transactions on Parallel and Distributed Systems， 2008， 19（11）： 1540-1552.

[5] LI K. Performance analysis of power-aware task scheduling algorithms on multiprocessor computers with dynamic voltage and speed[J]. IEEE Transactions on Parallel and Distributed Systems， 2008， 19（11）： 1484-1497.

[6] MANUMACHU R R， LASTOVETSKY A. Bi-objective optimization of data-parallel applications on homogeneous multicore clusters for performance and energy[J]. IEEE Transactions on Computers， 2018， 67（2）： 160-177.

[7] LI Y， NIU J， ATIQUZZAMAN M， et al. Energy-aware scheduling on heterogeneous multi-core systems with guaranteed probability[J]. Journal of Parallel and Distributed Computing， 2017， 103： 64-76.

[8] PAGANI S， PATHANIA A， SHAFIQUE M， et al. Energy efficiency for clustered heterogeneous multicores[J]. IEEE Transactions on Parallel and Distributed Systems， 2017， 28（5）： 1315-1330.

[9] CHENG D， ZHOU X， LAMA P， et al. Energy efficiency aware task assignment with DVFS in heterogeneous Hadoop clusters[J]. IEEE Transactions on Parallel and Distributed Systems， 2018， 29（1）： 70-82.

[10] ZHOU J， YAN J， CAO K， et al. Thermal-aware correlated two-level scheduling of real-time tasks with reduced processor energy on heterogeneous MPSoCs[J]. Journal of Systems Architecture， 2018， 82： 1-11.

[11] SUN W， SUGAWARA T. Heuristics and evaluations of energy-aware task mapping on heterogeneous multiprocessors[C]// Proceedings of the 2011 IEEE International Symposium on Parallel and Distributed Processing Workshops and PhD Forum. Piscataway： IEEE， 2011： 599-607.

[12] IZAKIAN H， ABRAHAM A， SNASEL V. Comparison of heuristics for scheduling independent tasks on heterogeneous distributed environments[C]// Proceedings of the 2009 International Joint Conference on Computational Sciences and Optimization. Piscataway： IEEE， 2009： 8-12.

[13] XU C， XIAO J， ZENG L， et al. An energy-aware dynamic algorithm based on variable interval DVFS technology[J]. Advanced Materials Research， 2014， 950： 185-195.

[14] THAMMAWICHAI M， KERRIGAN E C. Energy-efficient real-time scheduling for two-type heterogeneous multiprocessors[J]. Real-Time Systems， 2018， 54（1）： 132-165.

[15] LI D， WU J. Minimizing energy consumption for frame-based tasks on heterogeneous multiprocessor platforms[J]. IEEE Transactions on Parallel and Distributed Systems， 2015， 26（3）： 810-823.

[16] ALBERS S， ANTONIADIS A， GREINER G. On multi-processor speed scaling with migration[J]. Journal of Computer and System Sciences， 2015， 81（7）： 1194-1209.

[17] ANGEL E， BAMPIS E， KACEM F， et al. Speed scaling on parallel processors with migration[C]// Proceedings of the 18th International Conference of Parallel Processing， LNCS 7484. Berlin： Springer， 2012： 128-140.

[18] KHAN A A， ALI A， ZAKARYA M， et al. A migration aware scheduling technique for real-time aperiodic tasks over multiprocessor systems[J]. IEEE Access， 2019， 7： 27856-27873.